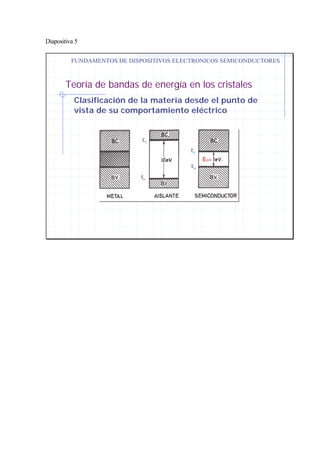
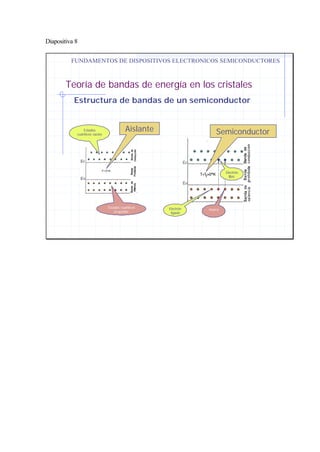
La teoría de bandas de energía explica cómo los niveles de energía discretos de los átomos aislados se convierten en bandas de energía continua en los cristales. Esto da lugar a tres tipos de comportamiento eléctrico: conductores, donde las bandas de valencia y conducción se solapan; aislantes, donde existe una gran separación entre las bandas; y semiconductores, con una pequeña separación entre bandas. La conductividad de los metales se debe al movimiento de los electrones libres en la banda de conducción, los cuales se