El documento aborda el cálculo y diseño de engranajes rectos, incluyendo aspectos geométricos, la interferencia, y el análisis de tensiones y fallas. Se presentan métodos de cálculo como los de Lewis y Buckingham, así como normas APMA e ISO para asegurar la resistencia y funcionamiento adecuado de los engranajes. Finalmente, se discuten las estructuras de montaje y el equilibrio dinámico necesario para un rendimiento óptimo.

1. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos

2. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
- sin interferencia
- grado recubr. adecuado
- bajo nivel ruido
- esfuerzos por Ntransmitida
- choques
- desgaste
Cálculo
geométrico
Cálculo
resistente
Dext, Dint
Grado recub.
Dp, b, Z, M,
tratam. Sup.
Dimensiones adecuadas

3. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Geometría

4. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
2
p
1
p
c
z
dπ
z
Dπ
p ==
p
2
p
1
d
d
z
D
z
p ==
Paso circunferencial
Paso Diametral
(Diametral Pitch)
2
p
1
pc
z
d
z
D
π
p
M ===
Módulo (normalizado)

5. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Geometría: normalización
Diámetro exterior: De = Dp + 2 a para a = M: Dext = (Z + 2) M

6. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos

7. Geometría: Interferencia
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
El problema de interferencia o socavación aparecerá cuando el
contacto se intente producir por debajo de la circunferencia base. En
este caso la trayectoria del punto de contacto, punto "C", al ser el
punto "I" centro instantáneo de rotación relativo, intenta penetrar en
el diente de la otra rueda produciendo la interferencia y si el punto "C"
fuese de la herramienta, produciría la socavación.

8. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
La circunferencia de cabeza de la rueda
"1" no debe pasar más allá del punto
"T2". En la figura se representa el radio
máximo de cabeza de la rueda "1" para
que no le produzca interferencia o
socavación a la rueda "2".
Esta interferencia limita la altura de la
cabeza del diente.

9. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Para engrane sin interferencia, contacto
debe realizarse dentro de los límites g-e
de la línea de presión.
Analizado geométricamente el diámetro
máximo exterior Ae, de la cabeza del
diente del engranaje conducido A está
dado por la expresión:
( ) ( )22
geAg +
( ) senrRcosR 2222
αα ++
Ae = R + ht =
2
RMZ
R =
2
rMZ
r = Maht =

10. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Para una relación conocida de a y conociendo el ángulo de
presión α, se puede obtener el número mínimo de dientes
Zr del piñón que puede engranar con una rueda de ZR
dientes, sin interferencia entre ambos. Para el mismo piñón
de Zr dientes, solo podrán engranar con él ruedas de menor
número de dientes que ZR, ya que para ruedas de mayor
cantidad de dientes habrá interferencia. Para un piñón de Zr
dientes y una cremallera ZR = ∞
( )
α2
R
Rr
2
r
sen
az4a
z2zz
+
=+
sen
2a
z 2r
α
=
La curva que expresa estos valores es
una hipérbola de asíntota horizontal
para ZR = ∞ (cremallera), que para el
caso de un diente de altura completa
(a = 1) y un ángulo de presión de 20°
vale 17, lo que significa que un piñón
con 17, o más dientes, no tendrá
interferencia con una cremallera o
con cualquier otra rueda.

11. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos

12. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Tipos de fallas

13. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
2 Zonas de
altas tensiones:
- Raíz del diente (tensión de flexión) -Punto de contacto (tensión superficial)

14. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Fuerzas y tensiones en los dientes
,
y

15. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
N = Ft V V = W R = 2 ∏ R n
Para N en HP, R en cm y v en m/s
resultan Ft, Fr y Fn en kg:
100.60
nR2
v
π
=
75
v.F
N t
=
71620
n.R.F
N t
=
n
N
R
71620
Ft =
αcos
1
n
N
R
71620
Fn =
αtg
n
N
R
71620
Fr =

16. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Buckingham
Métodos de cálculo: Flexión en la base
Lewis
Lewis-Barth
Métodos de cálculo: fatiga superficial
Buckingham
Norma AGMA
Norma AGMA

17. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Como el esfuerzo de compresión es
pequeño comparado con el de flexión, su
efecto sobre la resistencia del diente se
suele omitir en los cálculos
Métodos de cálculo: FLEXIÓN

18. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Métodos de cálculo: Wilfred Lewis (1892)
Hipótesis simplificativas:
- Diente empotrado en cuerpo del engrane
- Solicitación estática de flexión
- Carga uniforme en el ancho
- Carga aplicada en el extremo del diente
Objetivo:
Determinar la fuerza tangencial máxima que puede transmitir.

19. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Sólido de igual resistencia a la flexión
determina la sección de empotramiento
Momento flector:
Mf = Ft h = W σf
W (módulo resistente a la flexión, para rectángulo = b t² / 6)
f6
2t.b
h.tF σ=
p/sólido de igual resistencia:
σ=cte
Y como b=cte
2tCte2t
tF.6
b.
h ==
σ
que es la ecuación de una parábola

20. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
f6
2t.b
h.tF σ=
Como t y h son funciones del paso:
t²/6h = y p
y: factor de forma
función de Z p/valor particular de α
y del punto de aplicación de carga
tabulado p/perfiles normalizados

21. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Z Ø = 14.5° Ø = 20° Stub Ø = 20° Ø = 25°
10 0.056 0.064 0.083 0.076
12 0.067 0.078 0.099 0.088
13 0.070 0.083 0.103 0.093
14 0.072 0.088 0.108 0.098
15 0.075 0.092 0.111 0.102
16 0.077 0.094 0.115 0.106
17 0.080 0.096 0.117 0.109
18 0.083 0.098 0.120 0.112
19 0.087 0.100 0.123 0.115
20 0.090 0.102 0.125 0.118
21 0.092 0.104 0.127 0.120
23 0.094 0.106 0.130 0.124
25 0.097 0.108 0.133 0.128
27 0.100 0.111 0.136 0.131
30 0.102 0.114 0.139 0.135
34 0.104 0.118 0.142 0.140
38 0.107 0.122 0.145 0.144
43 0.110 0.126 0.147 0.148
50 0.112 0.130 0.151 0.152
60 0.114 0.134 0.154 0.156
75 0.116 0.138 0.158 0.161
100 0.118 0.142 0.161 0.166
150 0.120 0.146 0.165 0.171
300 0.122 0.150 0.170 0.176
Cremallera 0.124 0.154 0.175 0.180

22. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Ft = y b σf pf6
2t.b
h.tF σ= t²/6h = y pCon: y
Para obtener fuerza tangencial máxima admisible:
σf = σadm ≈ σrot/3
Fb = b y p σadm
n
N
R
71620
Ft =Para un diseño adecuado
Fb ≥ Ft

23. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Estimación del tamaño del engrane:
DISEÑO
Estimación de tamaño
(prediseño)
Verificación
Formulas empíricas, recomendaciones,
experiencia, métodos simples (Lewis)
Formulas más exactas (Buckingham),
normas (AGMA, ISO)

24. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
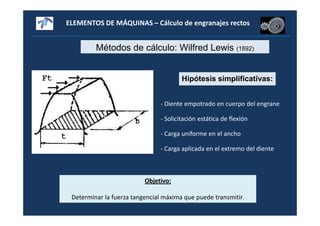
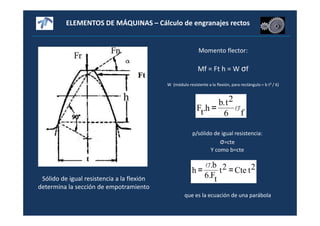
ecuación de Lewis para cálculos preliminares de diseño
Fb ≥ Ft
Partimos de la igualdad:
Fb = b[cm] y p[cm] σadm[Kg/cm2] = Ft [Kg] = 71620 N[HP] / (n[rpm] R[cm])
se considera como buena
la siguiente proporción:
2.5 p < b < 4 p ó 8 M < b < 12.5 M
Es decir, b = rrrr p
Fb = rrrr y p2 σadm
como Dp = ( p / π ) Z
Ft = 71620 N / [ n ( p Z / 2 π ) ]
Ft = 450.000 N / ( n p Z )

25. 3
adm Zny
N
6,76p
σρ
=
ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Fb = rrrr y p2 σadm
Ft = 450.000 N / ( n p Z )
Fb = Ft
- N y n, así como i, son condiciones a cumplir por el diseño
- Adoptar: α (generalmente 20°), material para el engranaje y Z
(según recomendaciones o criterios adecuados, por ejemplo, adoptar el número mínimo de dientes
necesarios para que no se produzca interferencia a fin de obtener las mínimas dimensiones exteriores)
Con p se calcula M, se redondea hasta el valor estandarizado inmediato superior;
después, por los valores de rrrr y Z, se determinan los diámetros de las ruedas y su ancho,
luego de acuerdo a las proporciones estándar se obtienen las restantes dimensiones:
diámetro exterior e interior, etc.
ya se tienen los engranajes para realizar las verificaciones según Buckingham o AGMA

26. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Esfuerzos en los apoyos
No importa la perfección con que se diseñe y fabrique un engranaje, éste debe ser
montado correctamente para tener un funcionamiento libre de fallas.
La función de un engrane es transmitir movimiento y/o potencia. La función del
soporte es crear un estado de equilibrio. Como un engrane es un cuerpo que gira o
está en movimiento, debe obtenerse un estado de “equilibrio dinámico”, es decir,
la totalidad de las fuerzas de trabajo y momentos de entrada deben ser igualados
por la totalidad de fuerzas y trabajo de salida.
“la suma de todas las fuerzas debe ser
igual a cero y la suma de todos los
momentos debe ser igual a cero”

27. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
todas las reacciones de los engranajes pueden
ser descompuestas en fuerza tangencial, fuerza
radial o separadora y empuje axial
sin importar el número de momentos
o de fuerzas que actúen sobre un
engrane, todos pueden concretarse a
dos tipos básicos de carga que son:
axial y radial

28. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos

29. ELEMENTOS DE MÁQUINAS – Cálculo de engranajes rectos
Hay dos tipos básicos de estructuras de montaje: doble soporte o entre apoyos (izquierda) y voladizo o cantilever (derecha).
Las reacciones de los apoyos actúan en dirección
opuesta a la de las cargas producidas por los
engranajes
Las cargas no actúan en el mismo sentido, la reacción
en el apoyo más cercano al punto de carga es opuesta
a dicha carga, la reacción en el más distante actúa en
el mismo sentido que el de la carga aplicada.