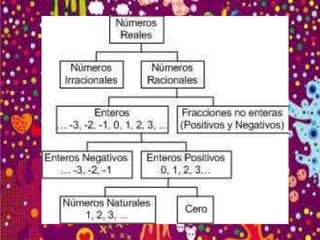
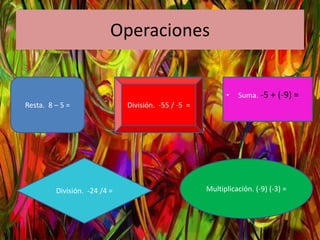
El documento define y proporciona ejemplos de números reales, irracionales y racionales. Los números reales incluyen números enteros, fracciones y números irracionales cuya expansión decimal nunca termina. Los números irracionales no pueden escribirse como fracciones y tienen expansiones decimales infinitas sin repetición. Los números racionales pueden escribirse como fracciones de números enteros. El documento también cubre desigualdades y operaciones básicas.

1. Equipo:
Rosa Isela
Rodolfo
Jorge Luis T.
Dulce Erlin
Ricardo

2. Números Reales
• Los números reales son los números que
se puede escribir con anotación decimal,
incluyendo aquellos que necesitan una
expansión decimal infinita. El conjunto de los
números reales contiene todos los números
enteros, positivos y negativos; todas las
fracciones; y todos los números irracionales,
aquellos cuyos desarrollos en decimales
nunca se repiten.

4. Números Irracionales
• Se le llama números irracionales a todos aquellos que no
pueden escribirse en forma de fracción debido a que el
decimal sigue indefinidamente sin repetirse.
Los números irracionales que no se pueden expresar como
una razón entre dos números.
• Un estudiante de Pitágoras llamado Hipaso descubrió
los números irracionales cuando intentaba escribir en
forma de fracción la raíz cuadrada de 2 sin conseguirlo,
por lo que definió esto como irracional.

5. Ejemplos de números irracionales
•
•
•
•
•
•
•
•
•
√31 = 5.5677643628300219221194712989185
√999 = 31.606961258558216545204213985699
√2 = 1.41427 indefinidamente
π = 3,14159265358979323846
√5 = 2.2360679774997896964091736687313
√7 = 2.6457513110645905905016157536393
√11 = 3.3166247903553998491149327366707
√13 = 3.6055512754639892931192212674705
√122 = 11.045361017187260774210913843344

6. Números Racionales
• Podemos empezar por decir que, un número racional es
una cifra o valor que puede ser referido como el
cociente de dos números enteros o más precisamente,
un número entero y un número natural positivo. Es decir
que es un número racional, es un número que se escribe
mediante una fracción.
• Los números racionales son números fraccionarios, sin
embargo los números enteros también pueden ser
expresados como fracción, por lo tanto también pueden
ser tomados como números racionales con el simple
hecho de dar un cociente entre el número entero y el
número 1 como denominador.

7. Ejemplos de números racionales
1. 2.5 = 25/ 10 = 10/4 = 5/2
2. 8/5 = 1.6
3. 1/7 = 0.142857142857
4. 1/60 = 0.01666
5. 5/7
6. 3=3/1
7. 15/5=3
8. −6=−6/1
9. 24/99
10.8/16

8. Desigualdad
• Una desigualdad expresa que dos valores no son iguales.
a ≠ b expresa que a es diferente de b
Hay otros símbolos especiales que muestran en qué sentido las
cosas no son iguales.
a < b dice que a es menor que b
a > b dice que a es mayor que b
(estos dos son conocidos como desigualdades estrictas)
a ≤ b significa que a es menor o igual que b
a ≥ b significa que a es mayor o igual que b.

9. Operaciones
•
Resta. 8 – 5 =
División. -24 /4 =
Suma. -5 + (-9) =
División. -55 / -5 =
Multiplicación. (-9) (-3) =