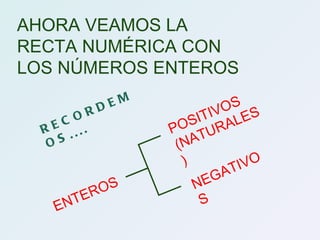
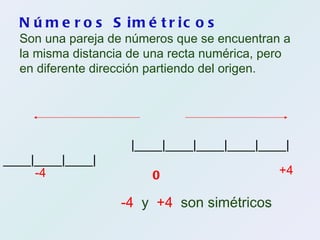
La recta numérica representa los números naturales de izquierda a derecha. Los números a la derecha de un número x son mayores que x, y los números a la izquierda son menores. El 0 es el único número sin antecesor ni sucesor. La recta numérica también incluye números enteros positivos y negativos, donde los números más a la derecha son mayores y los más a la izquierda son menores. Números simétricos como -4 y 4 están igualmente alejados del origen pero en direcciones opuestas.

1. LA RECTA NUMERICA ...sigamos practicando...

2. Los números naturales los podemos representar en una recta numérica

3. En el conjunto de números naturales se pueden establecer diferentes tipos de relaciones como por ejemplo >, <, =, …. > mayor que < menor que = igual que

4. En el gráfico anterior nos damos cuenta que 2 tiene como elemento sucesor 3 y como elemento antecesor 1 teniendo en cuenta que estamos estudiando el conjunto de los naturales. De esta manera podemos decir que el único elemento que no es sucesor de ninguno y que no tiene antecesor es el 0 .

5. También se podría afirmar que en una recta numérica todos los elementos que estén a la derecha de un elemento x son mayores que el y todos aquellos que estén a su izquierda son menores.

6. 0 y 1 están a la izquierda de 2, razón por la cual se cumple: 0 < 2 1 < 2 Lo mismo para los de la derecha: 3 > 2 10 > 2 EJEMPLO

7. AHORA VEAMOS LA RECTA NUMÉRICA CON LOS NÚMEROS ENTEROS ENTEROS POSITIVOS (NATURALES) NEGATIVOS RECORDEMOS....

8. Propiedades de la desigualdad: Un número es mayor cuando se encuentra más a la derecha que otro en la recta numérica: 0 -1 -2 -3 -4 derecha ...entonces 0  -4

9. Propiedades de la desigualdad: Un número es menor cuando se encuentra más a la izquierda que otro en la recta numérica: 0 -1 -2 -3 -4 izquierda ...entonces -2  1 1

10. Números Simétricos Son una pareja de números que se encuentran a la misma distancia de una recta numérica, pero en diferente dirección partiendo del origen. |____|____|____|____|____|____|____|____| -4 0 +4 -4 y +4 son simétricos

11. Propiedades de las Operaciones de Números Enteros -4 + 3 +5 + 3 -5 - 8 + 3 -10

13. Reglas de signos de sumas y restas Cantidades con signos iguales.- Se suman y se conserva el signo, ejemplo: -4 –3 = -7 suman mismo signo Cantidades con signos diferentes.- Se restan y se conserva el signo del mayor, ejemplo: -5 + 3 = -2 Signos diferentes Se restan y se conserva el signo del mayor

15. Reglas de signos de la multiplicación (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - Para llevar a cabo la multiplicación de signos se tomará en cuenta la siguiente tabla