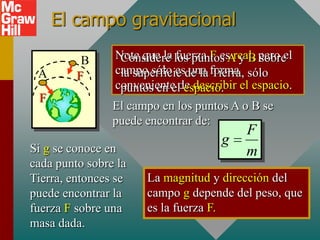
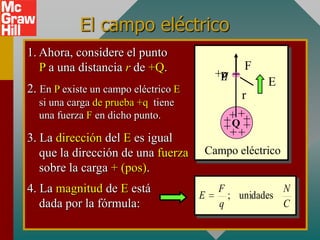
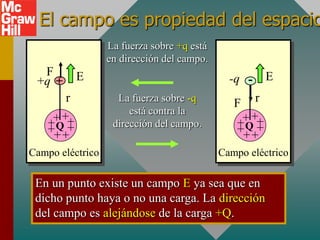
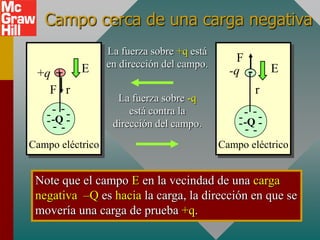
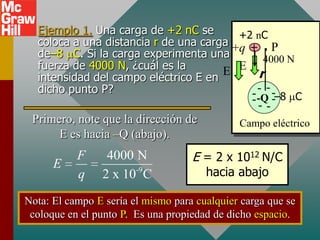
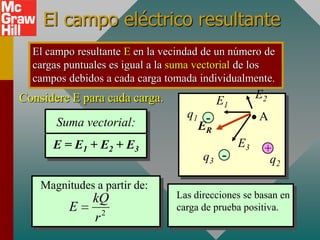
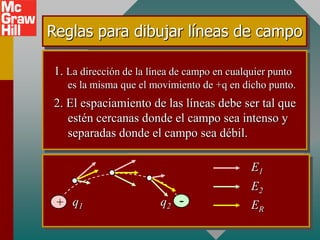
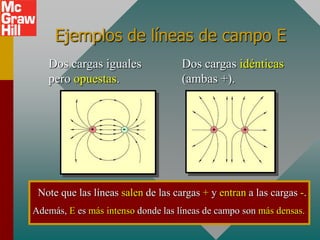
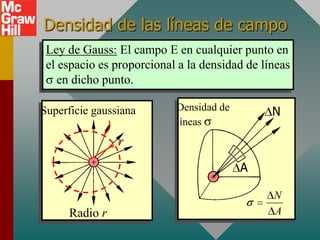
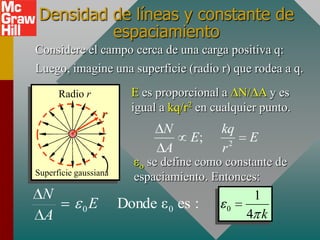
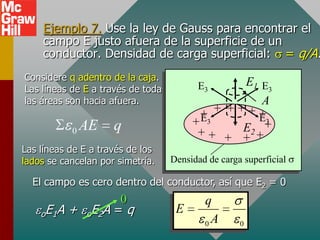
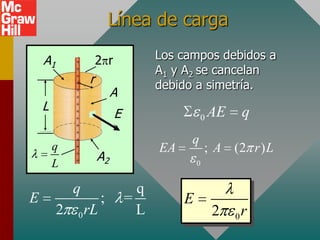
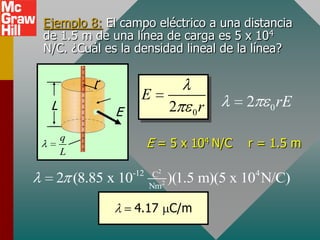
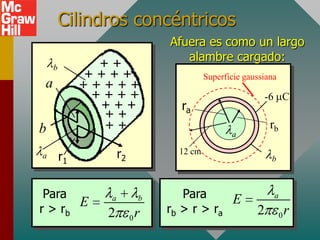
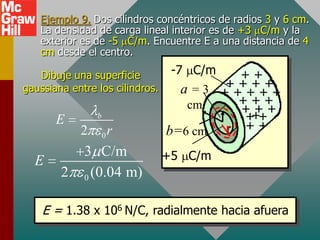
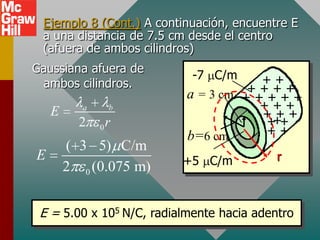
El documento presenta el concepto de campo eléctrico. Define el campo eléctrico como una propiedad del espacio que determina la fuerza experimentada por una carga en ese punto. Explica cómo calcular la intensidad del campo eléctrico a distintas distancias de una carga puntual y cómo dibujar las líneas de campo. También introduce la ley de Gauss para relacionar el número de líneas de campo que cruzan una superficie con la carga neta encerrada.

1. Campo eléctrico
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University

2. Objetivos: Después de terminar
esta unidad deberá:
• Definir el campo eléctrico y explicar qué
determina su magnitud y dirección.
• Escribir y aplicar fórmulas para la
intensidad del campo eléctrico a
distancias conocidas desde cargas
puntuales.
• Discutir las líneas de campo eléctrico y el
significado de la permitividad del espacio.
• Escribir y aplicar la ley de Gauss para campos en
torno a superficies con densidades de carga conocidas.

3. El concepto de campo
Un campo se define como una propiedad del espacio
en el que un objeto material experimenta una fuerza.
Sobre la Tierra, se dice que existe
P .
m
un campo gravitacional en P.
F
Puesto que una masa m experimenta
una fuerza descendente en dicho
punto.
¡No hay fuerza, no hay campo; no hay
campo, no hay fuerza!
La dirección del campo está determinada por la fuerza.

4. El campo gravitacional
B Note que la los puntos A y B pero el
Considere fuerza F es real, sobre
A F campo sólo esde la forma sólo
la superficie una Tierra,
conveniente de describir el espacio.
puntos en el espacio.
F
El campo en los puntos A o B se
puede encontrar de:
F
g
Si g se conoce en m
cada punto sobre la
Tierra, entonces se La magnitud y dirección del
puede encontrar la campo g depende del peso, que
fuerza F sobre una es la fuerza F.
masa dada.

5. El campo eléctrico
1. Ahora, considere el punto
P a una distancia r de +Q. F
P .
+q +
E
2. En P existe un campo eléctrico E
r
si una carga de prueba +q tiene
+
una fuerza F en dicho punto.
++ +
Q
++ ++
3. La dirección del E es igual
que la dirección de una fuerza Campo eléctrico
sobre la carga + (pos).
4. La magnitud de E está F N
E ; unidades
dada por la fórmula: q C

6. El campo es propiedad del espacio
La fuerza sobre +q está
en dirección del campo.
F . E . E
+q + -q -
r La fuerza sobre -q
F r
está contra la
+ ++
+Q + dirección del campo.
+ ++
+Q +
++ + ++ +
Campo eléctrico Campo eléctrico
En un punto existe un campo E ya sea que en
dicho punto haya o no una carga. La dirección
del campo es alejándose de la carga +Q.

7. Campo cerca de una carga negativa
La fuerza sobre +q está
F
.
+q + E en dirección del campo. .
-q - E
F r r
La fuerza sobre -q
- -Q- -
-
-- -
está contra la - --
- -Q -
- dirección del campo. --
-
Campo eléctrico Campo eléctrico
Note que el campo E en la vecindad de una carga
negativa –Q es hacia la carga, la dirección en que se
movería una carga de prueba +q.

8. La magnitud del campo E
La magnitud de la intensidad del campo eléctrico en un
punto en el espacio se define como la fuerza por unidad
de carga (N/C) que experimentaría cualquier carga de
prueba que se coloque en dicho punto.
Intensidad de F N
E ; unidades
campo eléctrico E q C
La dirección de E en un punto es la misma que la
dirección en que se movería una carga positiva SI
se colocara en dicho punto.

9. Ejemplo 1. Una carga de +2 nC se +2 nC
coloca a una distancia r de una carga +q + . P
de–8 C. Si la carga experimenta una 4000 N
fuerza de 4000 N, ¿cuál es la E E r
intensidad del campo eléctrico E en
dicho punto P? -- -- - -Q -–8 C
--
Primero, note que la dirección de Campo eléctrico
E es hacia –Q (abajo).
F 4000 N E = 2 x 1012 N/C
E
q -9
2 x 10 C hacia abajo
Nota: El campo E sería el mismo para cualquier carga que se
coloque en el punto P. Es una propiedad de dicho espacio.

10. Ejemplo 2. Un campo constante E de 40,000 N/C
se mantiene entre las dos placas paralelas.
¿Cuáles son la magnitud y dirección de la fuerza
sobre un electrón que pasa horizontalmente entre
las placas?
+ + + + + + + + +
El campo E es hacia abajo, y F- e- -
la fuerza sobre e- es arriba. e- - e- . E
F
E ; F qE - - - - - - - - -
q
-19 4 N
F qE (1.6 x 10 C)(4 x 10 C )
F = 6.40 x 10-15 N, hacia arriba

11. Campo E a una distancia r
desde una sola carga Q
Considere una carga de prueba +q E
F
colocada en P a una distancia r de Q.
+q +. P
.
P
La fuerza hacia afuera sobre +q r
es:
kQ
kQq ++ ++ E
+Q + r2
F 2 ++ +
r
Por tanto, el campo eléctrico E es:
F kQq r 2 kQ
E E 2
q q r

12. Ejemplo 3. ¿Cuál es la intensidad del campo
eléctrico E en el punto P, a una distancia de
3 m desde una carga negativa de–8 nC?
E=? . Primero, encuentre la magnitud:
P 9 Nm2 -9
r kQ (9 x 10 C2
)(8 x 10 C)
3m E 2 2
r (3 m)
-Q
-8 nC E = 8.00 N/C
La dirección es la misma que la fuerza sobre una
carga positiva si se colocase en el punto P: hacia –Q.
E = 8.00 N, hacia -Q

13. El campo eléctrico resultante
El campo resultante E en la vecindad de un número de
cargas puntuales es igual a la suma vectorial de los
campos debidos a cada carga tomada individualmente.
Considere E para cada carga. E1 E2
q1 - A
Suma vectorial: ER
E = E1 + E2 + E3 E3 +
q3 - q2
Magnitudes a partir de:
kQ Las direcciones se basan en
E carga de prueba positiva.
r2

14. Ejemplo 4. Encuentre el campo resultante en
el punto A debido a las cargas de –3 nC y +6
nC ordenadas como se muestra.
-3 nC
q1 - E para cada q se muestra
3 cm E 5 cm con la dirección dada.
1 +6 nC
+ kq1 kq2
E2 A 4 cm q2 E1 2
; E2 2
r1 r2
9 Nm2 -9 9 Nm2
(9 x 10 C2
)(3 x 10 C) (9 x 10 C2
)(6 x 10-9C)
E1 2
E2
(3 m) (4 m)2
Los signos de las cargas sólo se usan para encontrar la dirección de E

15. Ejemplo 4. (Cont.) Encuentre el campo
resultante en el punto A. Las magnitudes son:
9 Nm2
-3 nC
q1 - (9 x 10 C2
)(3 x 10-9C)
E1
(3 m)2
3 cm E 5 cm
1 +6 nC 9 Nm2
(9 x 10 C2
)(6 x 10-9C)
+ E2
E2 A 4 cm q2 (4 m)2
E1 = 3.00 N, oeste E2 = 3.38 N, norte
ER
A continuación, encuentre el vector resultante ER
E1
2 E1
ER E2 R12 ; tan E2
E2

16. Ejemplo 4. (Cont.) Encuentre el campo resultante
en el punto A con matemáticas vectoriales.
ER E1 = 3.00 N, oeste
E1 E2 = 3.38 N, norte
E2 Encuentre el vector resultante ER
3.38 N
E (3.00 N) 2
(3.38 N) 2
4.52 N; tan
3.00 N
= 48.40 N de O; o = 131.60
Campo resultante: ER = 4.52 N; 131.60

17. Líneas de campo eléctrico
Las líneas de campo eléctrico son líneas imaginarias que se
dibujan de tal forma que su dirección en cualquier punto es
la misma que la dirección del campo en dicho punto.
+ - --
++ +
Q
++ ++
- -Q -
--
-
Las líneas de campo se alejan de las cargas
positivas y se acercan a las cargas negativas.

18. Reglas para dibujar líneas de campo
1. La dirección de la línea de campo en cualquier punto
es la misma que el movimiento de +q en dicho punto.
2. El espaciamiento de las líneas debe ser tal que
estén cercanas donde el campo sea intenso y
separadas donde el campo sea débil.
E1
E2
+ q1 q2 - ER

19. Ejemplos de líneas de campo E
Dos cargas iguales Dos cargas idénticas
pero opuestas. (ambas +).
Note que las líneas salen de las cargas + y entran a las cargas -.
Además, E es más intenso donde las líneas de campo son más densas.

20. Densidad de las líneas de campo
Ley de Gauss: El campo E en cualquier punto en
el espacio es proporcional a la densidad de líneas
en dicho punto.
Superficie gaussiana Densidad de N
líneas
r
A
N
Radio r A

21. Densidad de líneas y constante de
espaciamiento
Considere el campo cerca de una carga positiva q:
Luego, imagine una superficie (radio r) que rodea a q.
Radio r E es proporcional a N/ A y es
igual a kq/r2 en cualquier punto.
r
N kq
E; E
A r2
se define como constante de
Superficie gaussiana
espaciamiento. Entonces:
N 1
0 E Donde ε 0 es : 0
A 4 k

22. Permitividad del espacio libre
La constante de proporcionalidad para la densidad de
líneas se conoce como permitividad y se define como:
1 C2
0 8.85 x 10-12 2
4 k N m
Al recordar la relación con la densidad de líneas se tiene:
N
0 E or N 0 E A
A
Sumar sobre toda el área A
N= oEA
da las líneas totales como:

23. Ejemplo 5. Escriba una ecuación para
encontrar el número total de líneas N que
salen de una sola carga positiva q.
Radio r Dibuje superficie gaussiana esférica:
r N E A y N EA
0 0
Sustituya E y A de:
kq q
E ; A = 4 r2
Superficie gaussiana r2 4 r2
q
N 0 EA 0 2
(4 r 2 ) N = oqA = q
4 r
El número total de líneas es igual a la carga encerrada q.

24. Ley de Gauss
Ley de Gauss: El número neto de líneas de campo
eléctrico que cruzan cualquier superficie cerrada en
una dirección hacia afuera es numéricamente igual a la
carga neta total dentro de dicha superficie.
N 0 EA q
Si q se representa como la carga q
positiva neta encerrada, la ley de EA
Gauss se puede rescribir como: 0

25. Ejemplo 6. ¿Cuántas líneas de campo
eléctrico pasan a través de la superficie
gaussiana dibujada abajo?
Superficie gaussiana
Primero encuentre la carga
NETA q encerrada por la
superficie: -4 C +8 C
q1 - q2 +
q = (+8 –4 – 1) = +3 C q4
-1 C
+
N q3 -
0 EA q +5 C
N = +3 C = +3 x 10-6 líneas

26. Ejemplo 6. Una esfera sólida (R = 6 cm) con una
carga neta de +8 C está adentro de un cascarón
hueco (R = 8 cm) que tiene una carga neta de–6
C. ¿Cuál es el campo eléctrico a una distancia de
12 cm desde el centro de la esfera sólida?
Dibuje una esfera gaussiana a un Superficie gaussiana
radio de 12 cm para encontrar E.
- -6 C
N
8cm - -
0 EA q
- +8 C -
6 cm
q = (+8 – 6) = +2 C -
q 12 cm - -
0 AE qnet ; E
0A
q 2 x 10-6C
E
0 (4 r 2 ) (8.85 x 10-12 Nm2
C 2 )(4 )(0.12 m)
2

27. Ejemplo 6 (Cont.) ¿Cuál es el campo
eléctrico a una distancia de 12 cm desde el
centro de la esfera sólida?
Dibuje una esfera gaussiana a un Superficie gaussiana
radio de 12 cm para encontrar E. -6 C
-
8cm - -
N 0 EA q - 6 cm
+8 C -
q = (+8 – 6) = +2 C -
12 cm - -
q
0 AE qnet ; E
0A
2 C
E 2
1.25 x 106 N C E = 1.25 MN/C
0 (4 r )

28. Carga sobre la superficie de un conductor
Dado que cargas iguales Superficie gaussiana justo
se repelen, se esperaría adentro del conductor
que toda la carga se
movería hasta llegar al
reposo. Entonces, de la
ley de Gauss. . . Conductor cargado
Como las cargas están en reposo, E = 0 dentro del
conductor, por tanto:
N 0 EA q or 0= q
Toda la carga está sobre la superficie; nada dentro del conductor

29. Ejemplo 7. Use la ley de Gauss para encontrar el
campo E justo afuera de la superficie de un
conductor. Densidad de carga superficial: = q/A.
Considere q adentro de la caja.
E3 E1 E
Las líneas de E a través de todas 3
las áreas son hacia afuera. A
+ + ++++
AE q + E3 E3
E2 +
0 ++ + + +
Las líneas de E a través de los
lados se cancelan por simetría. Densidad de carga superficial
El campo es cero dentro del conductor, así que E2 = 0
0 q
oE1A + oE2A = q E
0A 0

30. Ejemplo 7 (Cont.) Encuentre el campo justo
afuera de la superficie si = q/A = +2 C/m2.
Recuerde que los campos E1 E
E3 3
laterales se cancelan y el
campo interior es cero, de A
+ + ++++
modo que + E3 E3
E2 +
++ + + +
q
E1
0A 0 Densidad de carga superficial
2 x 10-6C/m2
E -12 Nm2 E = 226,000 N/C
8.85 x 10 C2

31. Campo entre placas paralelas
Cargas iguales y opuestas.
+ E1 - Campos E1 y E2 a la derecha.
+ -
Q1 + E2 - Q2 Dibuje cajas gaussianas en
+ - cada superficie interior.
E1
+ E2
- La ley de Gauss para cualquier caja
da el mismo campo (E1 = E2).
q
0 AE q E
0A 0

32. Línea de carga
A1 2 r Los campos debidos a
A1 y A2 se cancelan
r debido a simetría.
A
L
E 0 AE q
q
q
EA ; A (2 r ) L
L
A2 0
q q
E ; = E
2 0 rL L 2 0 r

33. Ejemplo 8: El campo eléctrico a una distancia
de 1.5 m de una línea de carga es 5 x 104
N/C. ¿Cuál es la densidad lineal de la línea?
r
E 2 rE
L E 2 0r
0
q
E = 5 x 104 N/C r = 1.5 m
L
-12 C2 4
2 (8.85 x 10 Nm2
)(1.5 m)(5 x 10 N/C)
4.17 C/m

34. Cilindros concéntricos
Afuera es como un largo
alambre cargado:
b ++
++++ Superficie gaussiana
a +++++
++++ -6 C
+++ ra
++
b ++ rb
a
a r1 r2 12 cm
b
Para a b Para E a
r > rb
E rb > r > ra
2 0r
2 0 r

35. Ejemplo 9. Dos cilindros concéntricos de radios 3 y 6 cm.
La densidad de carga lineal interior es de +3 C/m y la
exterior es de -5 C/m. Encuentre E a una distancia de 4
cm desde el centro.
Dibuje una superficie -7 C/m ++
gaussiana entre los cilindros. ++++
a=3 +++++
cm +++
+++
E b +
++
2 0 r b=6 cm r + +
3 C/m +5 C/m
E
2 0 (0.04 m)
E = 1.38 x 106 N/C, radialmente hacia afuera

36. Ejemplo 8 (Cont.) A continuación, encuentre E
a una distancia de 7.5 cm desde el centro
(afuera de ambos cilindros)
Gaussiana afuera de
-7 C/m ++
ambos cilindros. ++++
a = 3 cm + + + + +
a b +++
E +++
2 r +
++
0
b=6 cm ++
( 3 5) C/m
E +5 C/m r
2 0 (0.075 m)
E = 5.00 x 105 N/C, radialmente hacia adentro

37. Resumen de fórmulas
Intensidad de E
F kQ
Unidad es
N
2
campo eléctrico E: q r C
Campo eléctrico cerca kQ
E Suma vectorial
de muchas cargas: r 2
Ley de Gauss para q
distribuciones de carga. 0 EA q;
A

38. CONCLUSIÓN:
El campo eléctrico