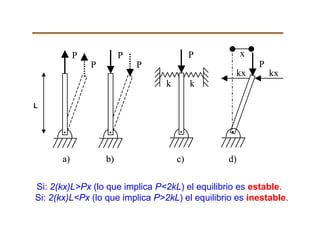
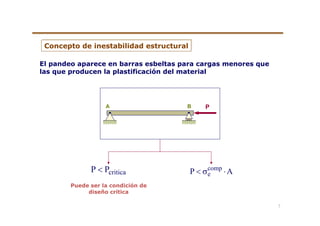
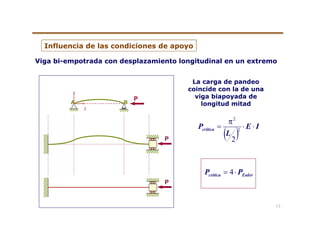
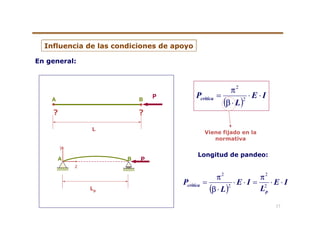
El documento trata sobre la inestabilidad elástica y el pandeo de piezas rectas. Explica que una hoja de sierra podría perder su estabilidad estructural para una carga menor que la que resistiría basada en su resistencia a la compresión. Luego presenta la teoría de primer orden de Euler para calcular la carga crítica de pandeo de una viga esbelta y discute cómo las condiciones de apoyo y la esbeltez mecánica afectan la carga crítica.