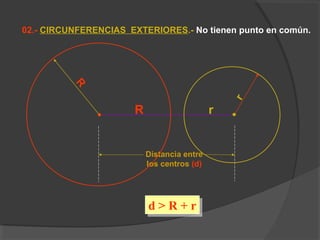
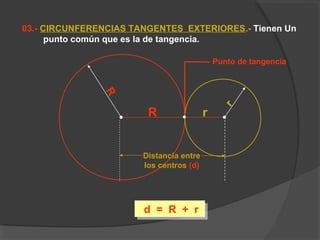
La circunferencia es un lugar geométrico de puntos equidistantes de un punto central llamado centro. Sus elementos incluyen el radio, diámetro, arco, cuerda y tangente. Algunas propiedades básicas son que un radio trazado al punto de tangencia es perpendicular a la tangente, y un radio perpendicular a una cuerda biseca la cuerda. Las posiciones relativas de dos circunferencias incluyen ser concéntricas, exteriores, tangentes exteriores/interiores, secantes, ortogonales e interiores

1. CIRCUNFERENCIA

2. CIRCUNFERENCIA.- Es un lugar geométrico
de un conjunto de infinitos puntos que
equidistan de un punto situado en el centro.

3. ELEMENTOS DE UNA CIRCUNFERENCIA
A B
M
N
Recta
tangente
Recta
secante
Flecha o
sagita
Diámetro
AB( )
Centro
T
Punto de tangencia
Q
P
Radio
Arco BQ
Cuerda PQ

4. PROPIEDADES BÁSICAS EN LA CIRCUNFERENCIA
01.-Radio trazado al punto de tangencia es
perpendicular a la recta tangente.
R
L
LR ⊥

5. 02.- Radio o diámetro perpendicular a una cuerda
la biseca (divide en dos segmentos congruentes).
P
Q
M
N
R
MQPMPQR =⇒⊥

6. 03.-Cuerdas paralelas determinan arcos congruentes
entre las paralelas.
A B
C D
 
mBDmACCD//AB:Si =⇒

7. 04.- A cuerdas congruentes en una misma circunferencia
les corresponden arcos congruentes.
A
B
C
D
Cuerdas congruentesArcos congruentes
Las cuerdas
equidistan del
centro
mCDmABCDAB:Si =⇒=

8. POSICIONES RELATIVAS DE DOS
CIRCUNFERENCIAS
01.- CIRCUNFERENCIAS CONCENTRICAS.- Tienen el mismo centro.
r
R
d = Cero ; d : distanciad = Cero ; d : distancia

9. R
r
Distancia entre
los centros (d)
02.- CIRCUNFERENCIAS EXTERIORES.- No tienen punto en común.
d > R + rd > R + r
R r

10. d = R + rd = R + r
03.- CIRCUNFERENCIAS TANGENTES EXTERIORES.- Tienen Un
punto común que es la de tangencia.
r
R
R r
Punto de tangencia
Distancia entre
los centros (d)

11. d
R
d = R - rd = R - r
04.- CIRCUNFERENCIAS TANGENTES INTERIORES.- Tienen un
punto en común que es la de tangencia.
d: Distancia entre los centros
R
r
Punto de
tangencia

12. 05.- CIRCUNFERENCIAS SECANTES.- Tienen dos puntos comunes
que son las intersecciones.
R r
( R – r ) < d < ( R + r )( R – r ) < d < ( R + r )
Distancia entre
los centros (d)

13. 06.- CIRCUNFERENCIAS ORTOGONALES.- Los radios son
perpendiculares en el punto de intersección.
d2
= R2
+ r2d2
= R2
+ r2
Distancia entre
los centros (d)
r
R

14. 06.- CIRCUNFERENCIAS INTERIORES.- No tienen puntos comunes.
R
r
d
d < R - rd < R - r d: Distancia entre los centros

15. 1.- Desde un punto exterior a una circunferencia se puede
trazar dos rayos tangentes que determinan dos
segmentos congruentes.
PROPIEDADES DE LAS TANGENTES
AP = PBAP = PB
A
B
P
R
R
α
α

16. 2.- TANGENTES COMUNES EXTERIORES.- Son congruentes
AB = CDAB = CD
A
B
C
D
R
R
r
r

17. 3.- TANGENTES COMUNES INTERIORES.- Son congruentes.
AB = CDAB = CD
A
B
C
DR
R
r
r

18. GRACIAS