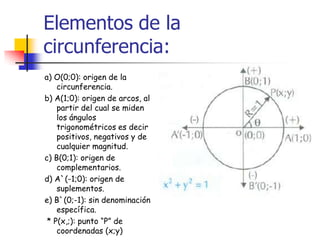
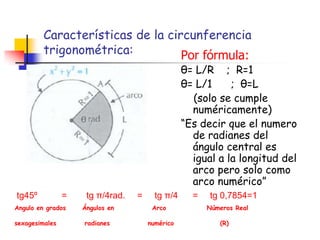
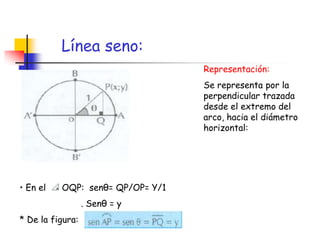
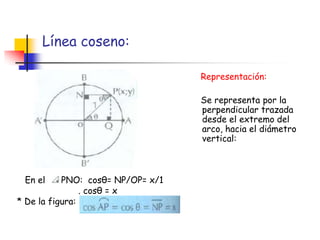
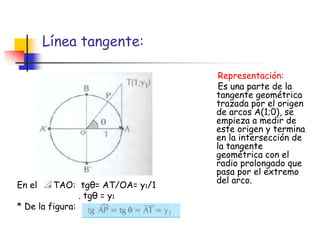
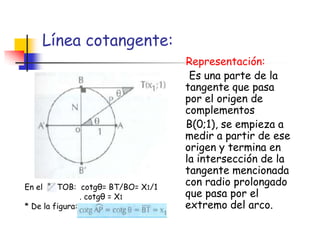
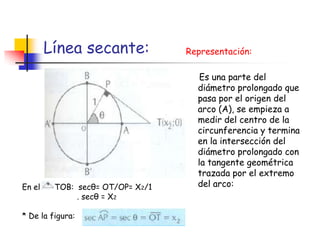
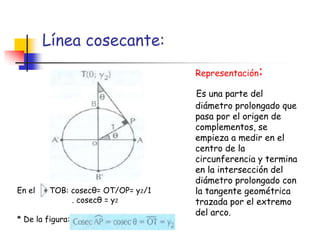
La circunferencia trigonométrica tiene un radio de 1 unidad y está centrada en el origen de coordenadas. Representa las líneas trigonométricas y tiene elementos como el origen de arcos y complementarios. Las líneas seno, coseno y tangente representan las relaciones entre los segmentos divididos por la circunferencia y el radio, mientras que las líneas cotangente, secante y cosecante usan diámetros prolongados.

2. Definición:
Es una circunferencia
inscrita en un sistema de
coordenadas rectangulares
(x;y) cuyo centro coincide
con el origen de dicho
sistema. Esta circunferencia
tiene como característica
fundamental, el valor del
radio que es la unidad (R=1).
Esta circunferencia
trigonométrica sirve para
representar a las líneas
trigonométricas.

3. Elementos de la
circunferencia:
a) O(0;0): origen de la
circunferencia.
b) A(1;0): origen de arcos, al
partir del cual se miden
los ángulos
trigonométricos es decir
positivos, negativos y de
cualquier magnitud.
c) B(0;1): origen de
complementarios.
d) A`(-1;0): origen de
suplementos.
e) B`(0;-1): sin denominación
específica.
* P(x,;): punto “P” de
coordenadas (x;y)

4. Propiedades convencionales:
a) Radio de la circunferencia igual a la UNIDAD (R=1)
b) Cuatro cuadrantes numerados, cada uno de los cuales
mide 90º, 100g ó π/2rad.
c) Se adoptan los signos de los ejes coordenadas o sea los
segmentos y son positivos y
son negativos.

5. Características de la circunferencia
trigonométrica:
Por fórmula:
θ= L/R ; R=1
θ= L/1
; θ=L
(solo se cumple
numéricamente)
“Es decir que el numero
de radianes del
ángulo central es
igual a la longitud del
arco pero solo como
arco numérico”
tg45º
=
Angulo en grados
sexagesimales
tg π/4rad.
=
tg π/4
Ángulos en
Arco
radianes
numérico
=
tg 0,7854=1
Números Real
(R)

7. Línea seno:
Representación:
Se representa por la
perpendicular trazada
desde el extremo del
arco, hacia el diámetro
horizontal:
• En el
OQP: senθ= QP/OP= Y/1
. Senθ = y
* De la figura:

8. Línea coseno:
Representación:
Se representa por la
perpendicular trazada
desde el extremo del
arco, hacia el diámetro
vertical:
En el
PNO: cosθ= NP/OP= x/1
. cosθ = x
* De la figura:

9. Línea tangente:
En el
TAO: tgθ= AT/OA= y1/1
. tgθ = y1
* De la figura:
Representación:
Es una parte de la
tangente geométrica
trazada por el origen
de arcos A(1;0), se
empieza a medir de
este origen y termina
en la intersección de
la tangente
geométrica con el
radio prolongado que
pasa por el extremo
del arco.

10. Línea cotangente:
En el
TOB: cotgθ= BT/BO= X1/1
. cotgθ = X1
* De la figura:
Representación:
Es una parte de la
tangente que pasa
por el origen de
complementos
B(0;1), se empieza a
medir a partir de ese
origen y termina en
la intersección de la
tangente mencionada
con radio prolongado
que pasa por el
extremo del arco.

11. Línea secante:
En el
TOB: secθ= OT/OP= X2/1
. secθ = X2
* De la figura:
Representación:
Es una parte del
diámetro prolongado que
pasa por el origen del
arco (A), se empieza a
medir del centro de la
circunferencia y termina
en la intersección del
diámetro prolongado con
la tangente geométrica
trazada por el extremo
del arco:

12. Línea cosecante:
Representación:
En el
TOB: cosecθ= OT/OP= y2/1
. cosecθ = y2
* De la figura:
Es una parte del
diámetro prolongado que
pasa por el origen de
complementos, se
empieza a medir en el
centro de la
circunferencia y termina
en la intersección del
diámetro prolongado con
la tangente geométrica
trazada por el extremo
del arco.