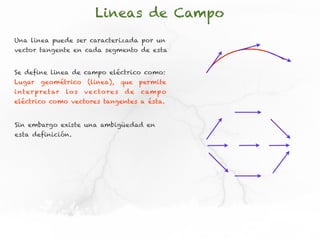
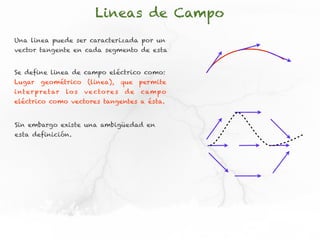
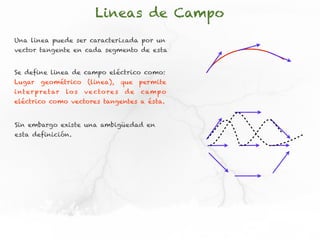
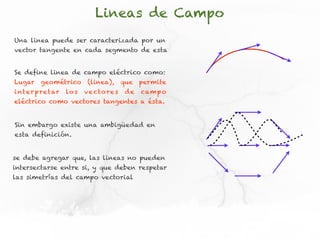
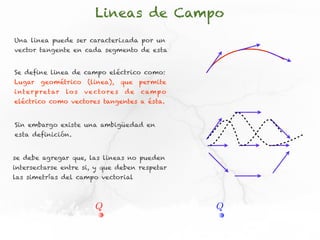
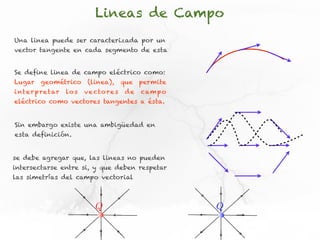
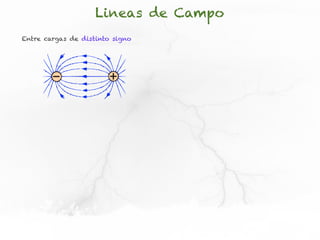
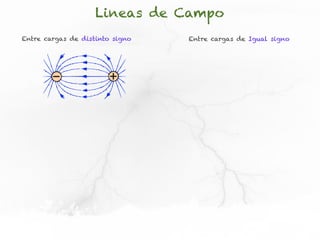
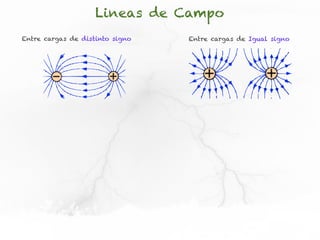
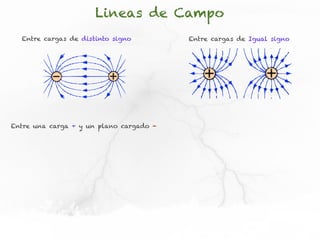
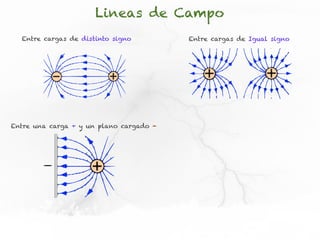
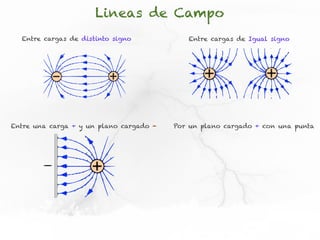
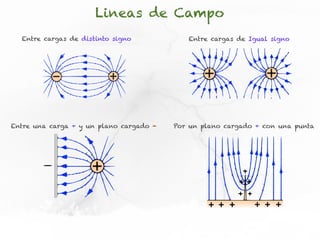
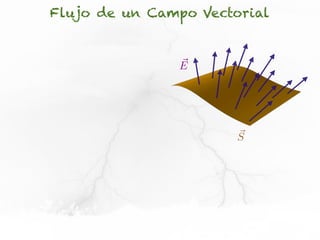
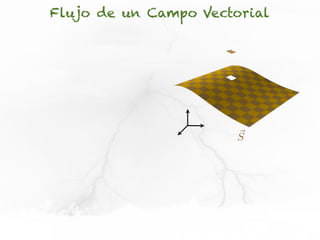
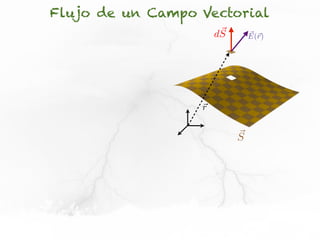
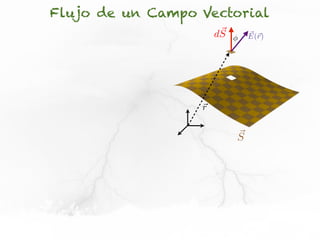
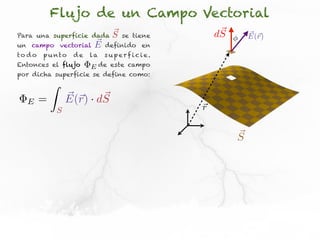
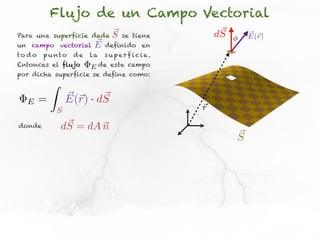
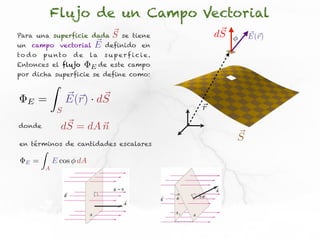
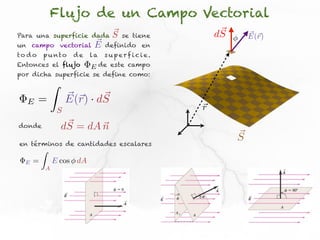
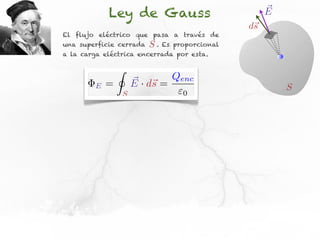
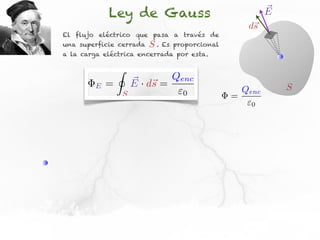
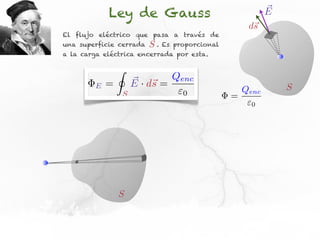
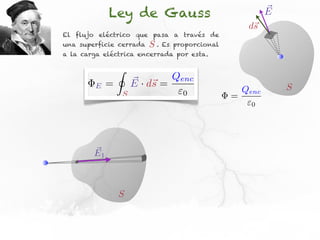
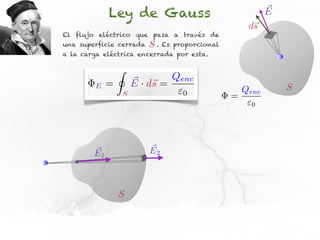
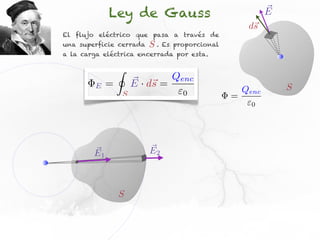
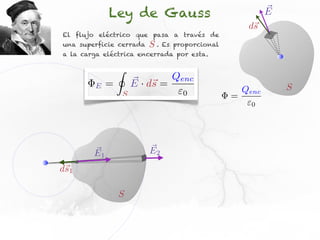
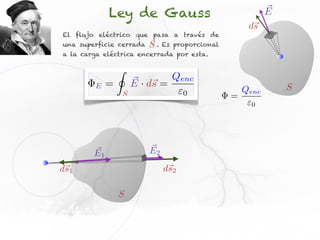
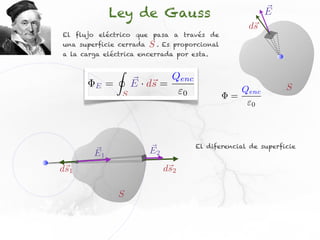
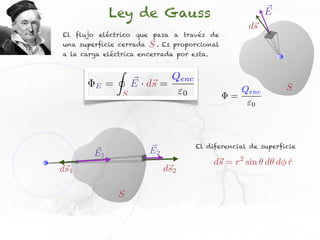
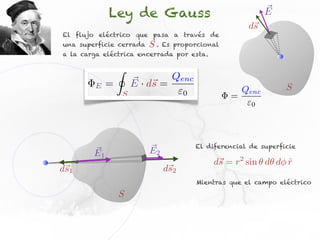
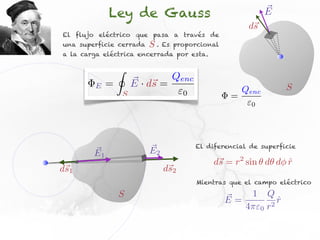
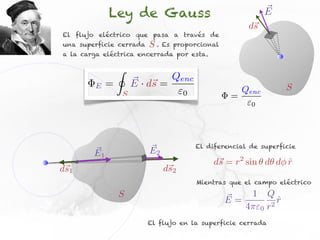
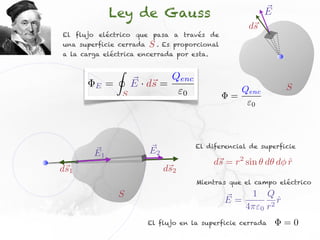
El documento presenta conceptos sobre líneas de campo eléctrico y flujo de campo vectorial. Define línea de campo eléctrico como una línea tangente al vector campo eléctrico en cada punto. Explica que el flujo de campo a través de una superficie se define como la integral del producto punto del campo y la superficie elemental a lo largo de toda la superficie.

1. Física General II
Lineas de Campo, Ley de
Gauss
Clase 3
Prof. Maximiliano A. Rivera
Depto de Física, UTFSM
maximiliano.rivera@usm.cl

2. Lineas de Campo

3. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta

4. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta

5. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.

6. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.
Sin embargo existe una ambigüedad en
esta definición.

7. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.
Sin embargo existe una ambigüedad en
esta definición.

8. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.
Sin embargo existe una ambigüedad en
esta definición.

9. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.
Sin embargo existe una ambigüedad en
esta definición.

10. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.
Sin embargo existe una ambigüedad en
esta definición.
se debe agregar que, las lineas no pueden
intersectarse entre si, y que deben respetar
las simetrías del campo vectorial

11. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.
Sin embargo existe una ambigüedad en
esta definición.
se debe agregar que, las lineas no pueden
intersectarse entre si, y que deben respetar
las simetrías del campo vectorial
Q Q

12. Lineas de Campo
Una linea puede ser caracterizada por un
vector tangente en cada segmento de esta
Se define linea de campo eléctrico como:
Lugar geométrico (linea), que permite
i nt e r p re t ar lo s v e cto re s de cam p o
eléctrico como vectores tangentes a ésta.
Sin embargo existe una ambigüedad en
esta definición.
se debe agregar que, las lineas no pueden
intersectarse entre si, y que deben respetar
las simetrías del campo vectorial
Q Q

13. Lineas de Campo

14. Lineas de Campo
Entre cargas de distinto signo

15. Lineas de Campo
Entre cargas de distinto signo

16. Lineas de Campo
Entre cargas de distinto signo Entre cargas de Igual signo

17. Lineas de Campo
Entre cargas de distinto signo Entre cargas de Igual signo

18. Lineas de Campo
Entre cargas de distinto signo Entre cargas de Igual signo
Entre una carga + y un plano cargado -

19. Lineas de Campo
Entre cargas de distinto signo Entre cargas de Igual signo
Entre una carga + y un plano cargado -

20. Lineas de Campo
Entre cargas de distinto signo Entre cargas de Igual signo
Entre una carga + y un plano cargado - Por un plano cargado + con una punta

21. Lineas de Campo
Entre cargas de distinto signo Entre cargas de Igual signo
Entre una carga + y un plano cargado - Por un plano cargado + con una punta

22. Flujo de un Campo Vectorial

23. Flujo de un Campo Vectorial
E

24. Flujo de un Campo Vectorial
E
S

25. Flujo de un Campo Vectorial
E
S

26. Flujo de un Campo Vectorial
S

27. Flujo de un Campo Vectorial
S

28. Flujo de un Campo Vectorial
r
S

29. Flujo de un Campo Vectorial
dS
r
S

30. Flujo de un Campo Vectorial
dS ~ r
E(~)
r
S

31. Flujo de un Campo Vectorial
dS ~ r
E(~)
r
S

32. Flujo de un Campo Vectorial
Para una superficie dada S se tiene dS ~ r
E(~)
un campo vectorial E definido en
to d o p u nto de la s u p er f i c i e.
Entonces el flujo E de este campo
por dicha superficie se define como:
Z
E = E(r) · dS
S r
S

33. Flujo de un Campo Vectorial
Para una superficie dada S se tiene dS ~ r
E(~)
un campo vectorial E definido en
to d o p u nto de la s u p er f i c i e.
Entonces el flujo E de este campo
por dicha superficie se define como:
Z
E = E(r) · dS
S r
donde dS = dA n
S

34. Flujo de un Campo Vectorial
Para una superficie dada S se tiene dS ~ r
E(~)
un campo vectorial E definido en
to d o p u nto de la s u p er f i c i e.
Entonces el flujo E de este campo
por dicha superficie se define como:
Z
E = E(r) · dS
S r
donde dS = dA n
en términos de cantidades escalares
S

35. Flujo de un Campo Vectorial
Para una superficie dada S se tiene dS ~ r
E(~)
un campo vectorial E definido en
to d o p u nto de la s u p er f i c i e.
Entonces el flujo E de este campo
por dicha superficie se define como:
Z
E = E(r) · dS
S r
donde dS = dA n
en términos de cantidades escalares
S
Z
E = E cos dA
A

36. Flujo de un Campo Vectorial
Para una superficie dada S se tiene dS ~ r
E(~)
un campo vectorial E definido en
to d o p u nto de la s u p er f i c i e.
Entonces el flujo E de este campo
por dicha superficie se define como:
Z
E = E(r) · dS
S r
donde dS = dA n
en términos de cantidades escalares
S
Z
E = E cos dA
A

37. Flujo de un Campo Vectorial
Para una superficie dada S se tiene dS ~ r
E(~)
un campo vectorial E definido en
to d o p u nto de la s u p er f i c i e.
Entonces el flujo E de este campo
por dicha superficie se define como:
Z
E = E(r) · dS
S r
donde dS = dA n
en términos de cantidades escalares
S
Z
E = E cos dA
A

38. Flujo de un Campo Vectorial
Para una superficie dada S se tiene dS ~ r
E(~)
un campo vectorial E definido en
to d o p u nto de la s u p er f i c i e.
Entonces el flujo E de este campo
por dicha superficie se define como:
Z
E = E(r) · dS
S r
donde dS = dA n
en términos de cantidades escalares
S
Z
E = E cos dA
A

39. Ley de Gauss

40. Ley de Gauss
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.

41. Ley de Gauss
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ =
S 0

42. Ley de Gauss
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0

43. Ley de Gauss
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0

44. Ley de Gauss
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0

45. Ley de Gauss
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0

46. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0

47. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0

48. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
S

49. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
S

50. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
S

51. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
S

52. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
E1
S

53. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
E1 E2
S

54. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
E1 E2
S

55. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
E1 E2
ds1
S

56. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
E1 E2
ds1 ds2
S

57. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
El diferencial de superficie
E1 E2
ds1 ds2
S

58. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
El diferencial de superficie
E1 E2
d⇤ = r2 sin d d⇥ r
s ˆ
ds1 ds2
S

59. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
El diferencial de superficie
E1 E2
d⇤ = r2 sin d d⇥ r
s ˆ
ds1 ds2
Mientras que el campo eléctrico
S

60. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
El diferencial de superficie
E1 E2
d⇤ = r2 sin d d⇥ r
s ˆ
ds1 ds2
Mientras que el campo eléctrico
S ⇤ 1 Q
E= 2
r
ˆ
4 ⇥0 r

61. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
El diferencial de superficie
E1 E2
d⇤ = r2 sin d d⇥ r
s ˆ
ds1 ds2
Mientras que el campo eléctrico
S ⇤ 1 Q
E= 2
r
ˆ
4 ⇥0 r
El flujo en la superficie cerrada

62. Ley de Gauss E
ds
El flujo eléctrico que pasa a través de
una superficie cerrada S. Es proporcional
a la carga eléctrica encerrada por esta.
I
⇥ s Qenc
E = E · d⇥ = S
S 0 Qenc
=
0
El diferencial de superficie
E1 E2
d⇤ = r2 sin d d⇥ r
s ˆ
ds1 ds2
Mientras que el campo eléctrico
S ⇤ 1 Q
E= 2
r
ˆ
4 ⇥0 r
El flujo en la superficie cerrada =0

63. Análisis
La figura ilustra seis cargas puntuales que
e stán en el mismo plan o. Hay cinco
superficies Gaussianas S1, S2, S3, S4 y S5,
que encierran, cada una, parte de este
plano. Clasifique las cinco superficies según
su flujo eléctrico en orden descendente (de
mayor a menor)

64. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.

65. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss

66. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico
tiene cierta simetría espacial

67. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico
tiene cierta simetría espacial
Esférica en este caso

68. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico
tiene cierta simetría espacial
r
Esférica en este caso

69. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico
tiene cierta simetría espacial
E
r
Esférica en este caso

70. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico
tiene cierta simetría espacial
E
r
Esférica en este caso

71. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico
tiene cierta simetría espacial
E
ds
r
Esférica en este caso

72. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial
E
ds
r
Esférica en este caso

73. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial I
E E = ~ s
E · d~
ds
r
Esférica en este caso

74. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial I
E E = ~ s
E · d~
ds Z
= E r · r dA
ˆ ˆ
r
Esférica en este caso

75. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial I
E E = ~ s
E · d~
ds Z
= E r · r dA
ˆ ˆ
Z
r =E dA
Esférica en este caso

76. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial I
E E = ~ s
E · d~
ds Z
= E r · r dA
ˆ ˆ
Z
r =E dA = E 4⇡r 2
Esférica en este caso

77. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial I
E E = ~ s
E · d~
ds Z
= E r · r dA
ˆ ˆ
Z
r Qenc2
=E dA = E 4⇡r =
"0
Esférica en este caso

78. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial I
E E = ~ s
E · d~
ds Idéntico a la deducción a
Z
través de ley de Coulomb = E r · r dA
ˆ ˆ
Z
r Qenc2
=E dA = E 4⇡r =
"0
Esférica en este caso

79. Ley de Gauss
El flujo eléctrico que pasa a través I
de una superficie cerrada S . Es
E = ⇥ · d⇥ = Qenc
E s
proporcional a la carga eléctrica S 0
encerrada por esta.
Utilidades de la ley de Gauss
Solo sabemos que el campo eléctrico Así tenemos que:
tiene cierta simetría espacial I
E E = ~ s
E · d~
ds Idéntico a la deducción a
Z
través de ley de Coulomb = E r · r dA
ˆ ˆ
~ 1 Q Z
r E= 2
r
ˆ Qenc2
4⇡"0 r =E dA = E 4⇡r =
"0
Esférica en este caso

80. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0

81. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0

82. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
r
p

83. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
r
p

84. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
s3 r
p
s2

85. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r
p
s2

86. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
p E = ~ ~
E · d S3
s3
s2

87. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2

88. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?

89. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
debemos considerar un largo del cilindro

90. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
L
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
debemos considerar un largo del cilindro

91. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
L
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
Q= L
debemos considerar un largo del cilindro

92. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
L
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
Q= L
debemos considerar un largo del cilindro
Z
E =E r d dz
s3

93. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
L
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
Q= L
debemos considerar un largo del cilindro
Z
E =E r d dz
s3
E = E 2⇡L r

94. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
L
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
Q= L
debemos considerar un largo del cilindro
Z
E =E r d dz
s3
L
E = E 2⇡L r =
"0

95. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
L
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
Q= L
debemos considerar un largo del cilindro
Z
E =E r d dz
s3
L
E = E 2⇡L r =
"0
~
E= r
ˆ
2⇡"0 r

96. Utilidades de la ley de Gauss
I
⇥ s Qenc
E = E · d⇥ =
S 0
s1
Por simetría del problema, sólo s3 contribuye
s3 r Z
L
p E = ~ ~
E · d S3 donde ~
dS3 = r d dz r
ˆ
s3
s2
¿Cuanto es la carga encerrada?
Q= L
debemos considerar un largo del cilindro
Z
E =E r d dz
s3
L
E = E 2⇡L r =
"0
~
E= r
ˆ
2⇡"0 r
¿Miró el ejemplo 21.11 de Sears Zemansky ?