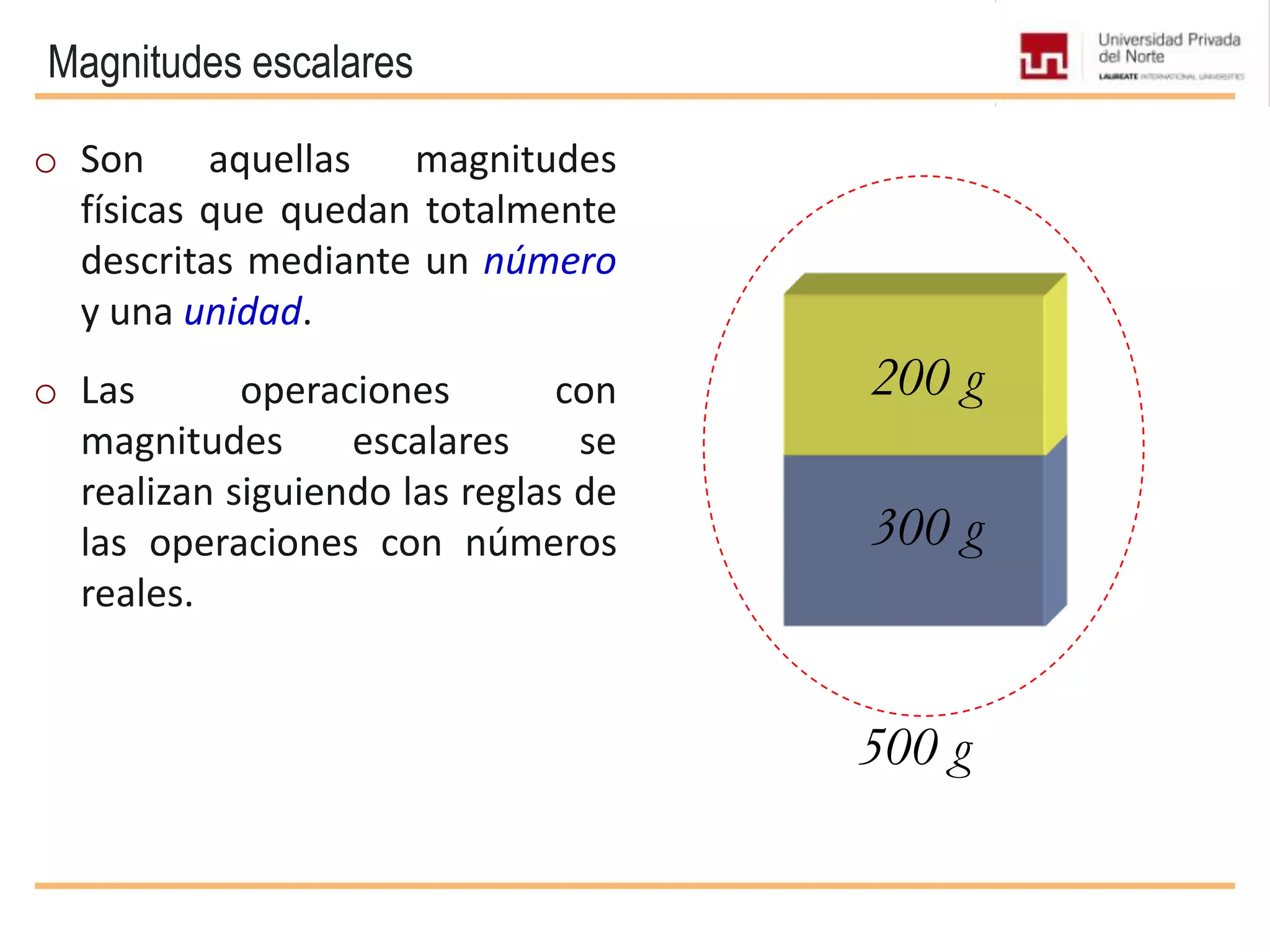
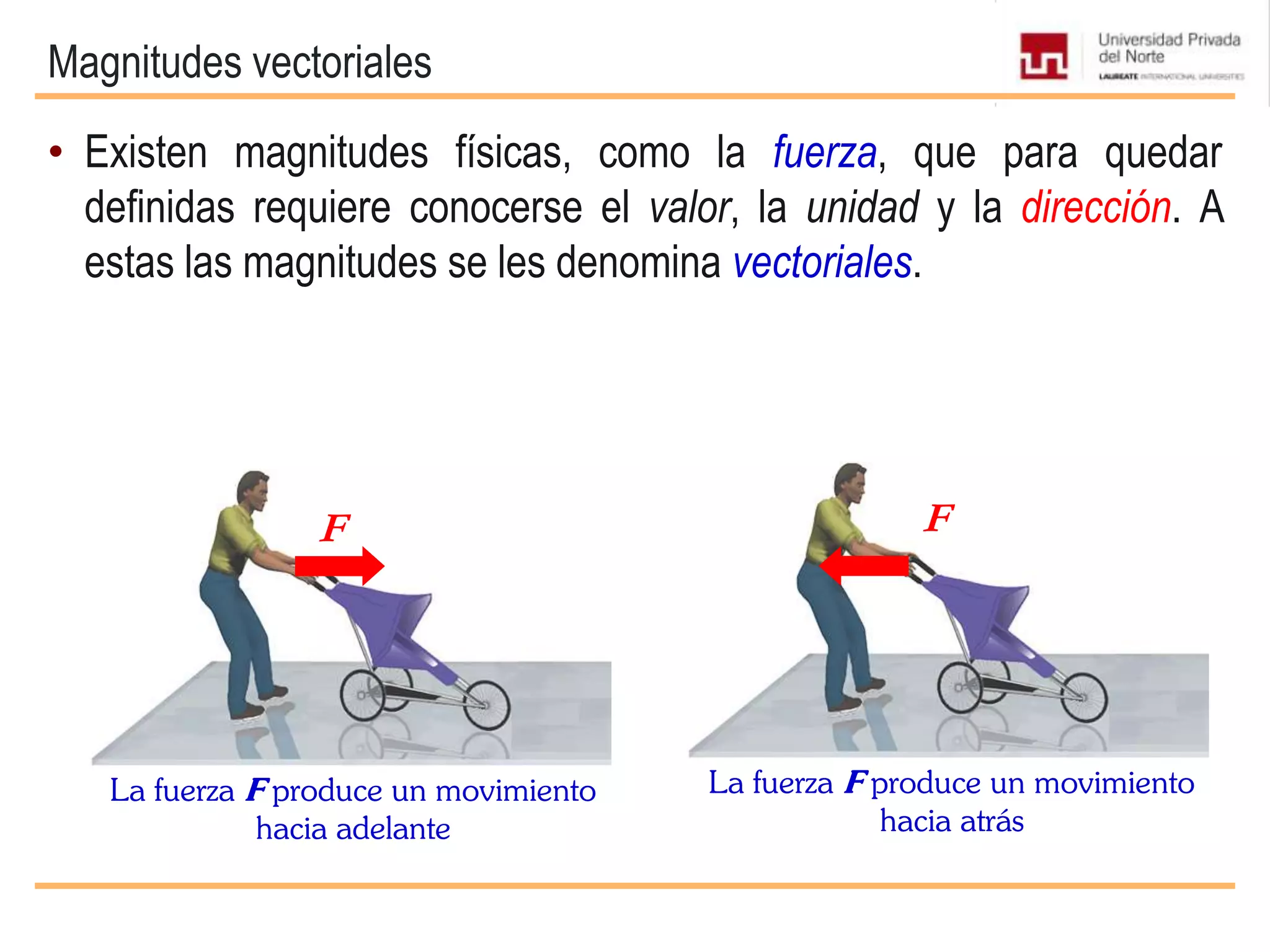
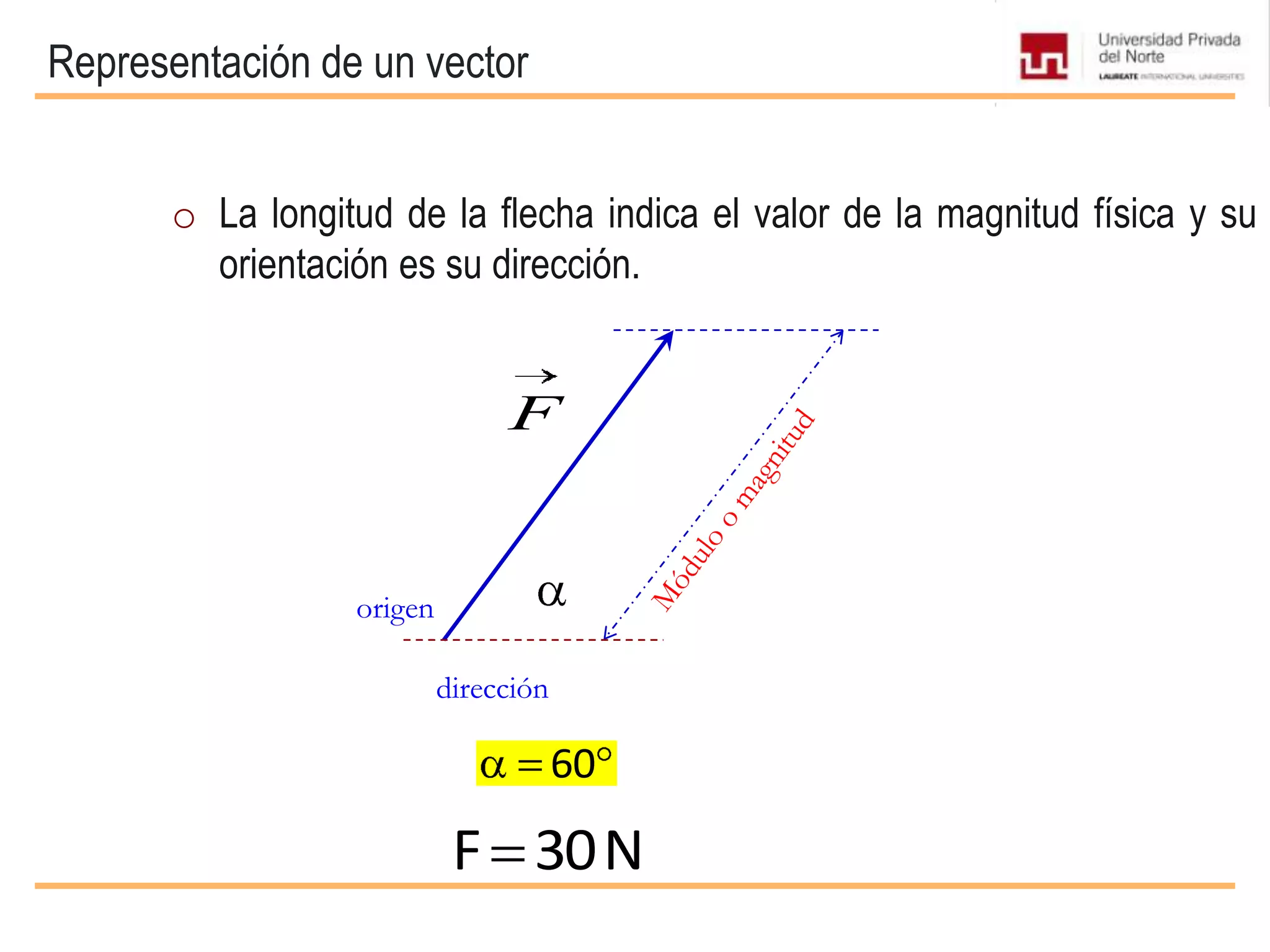
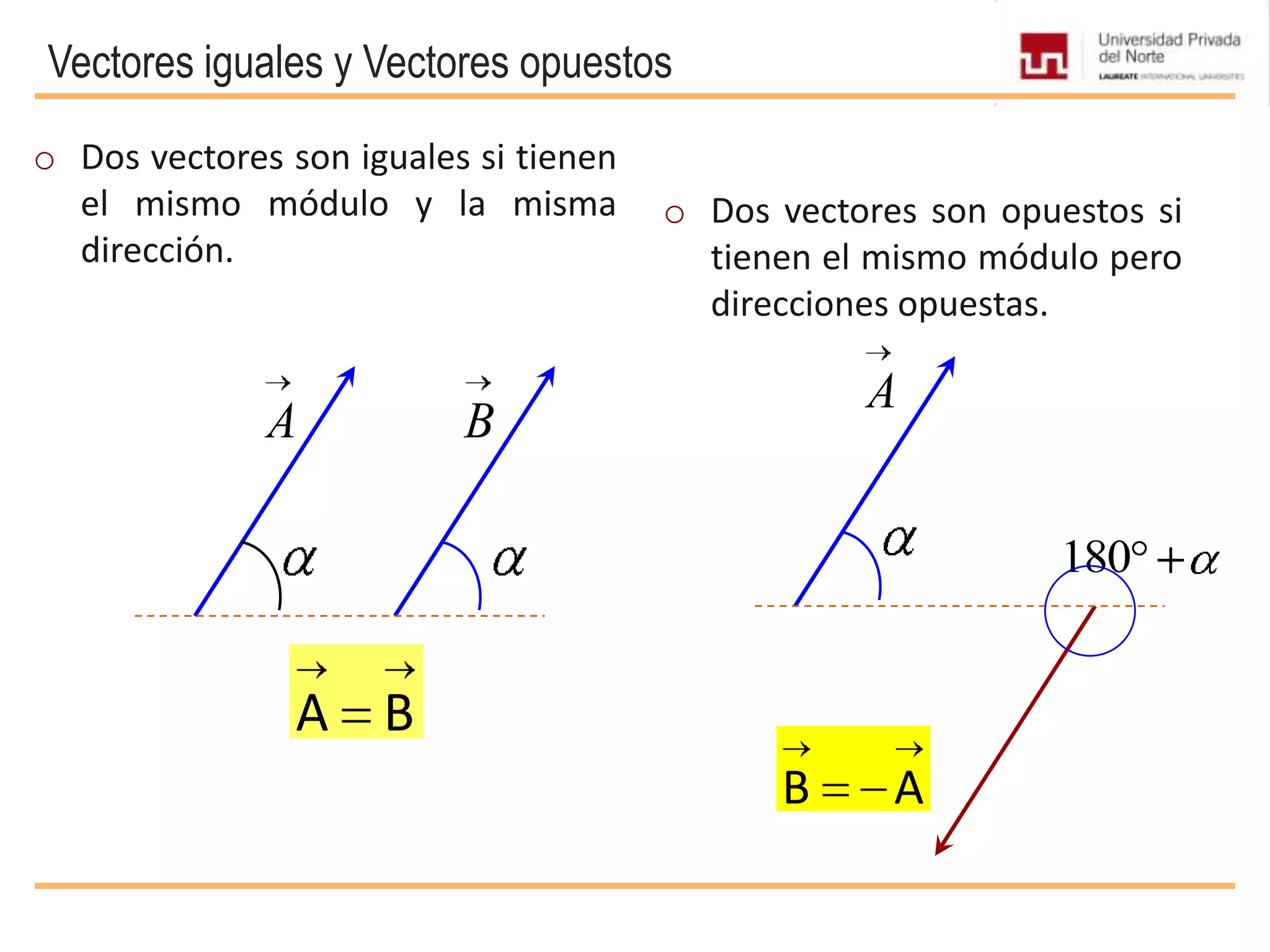
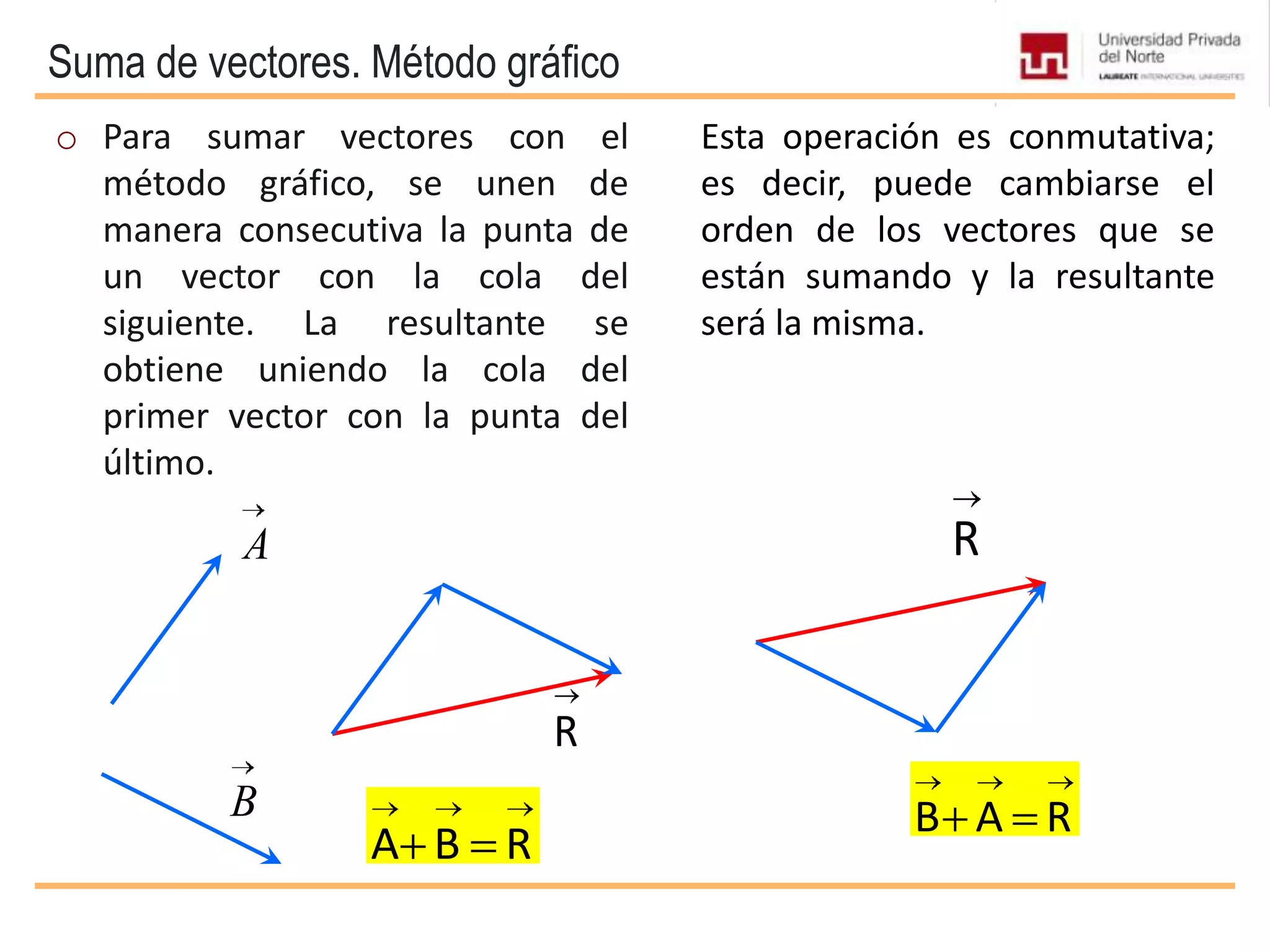
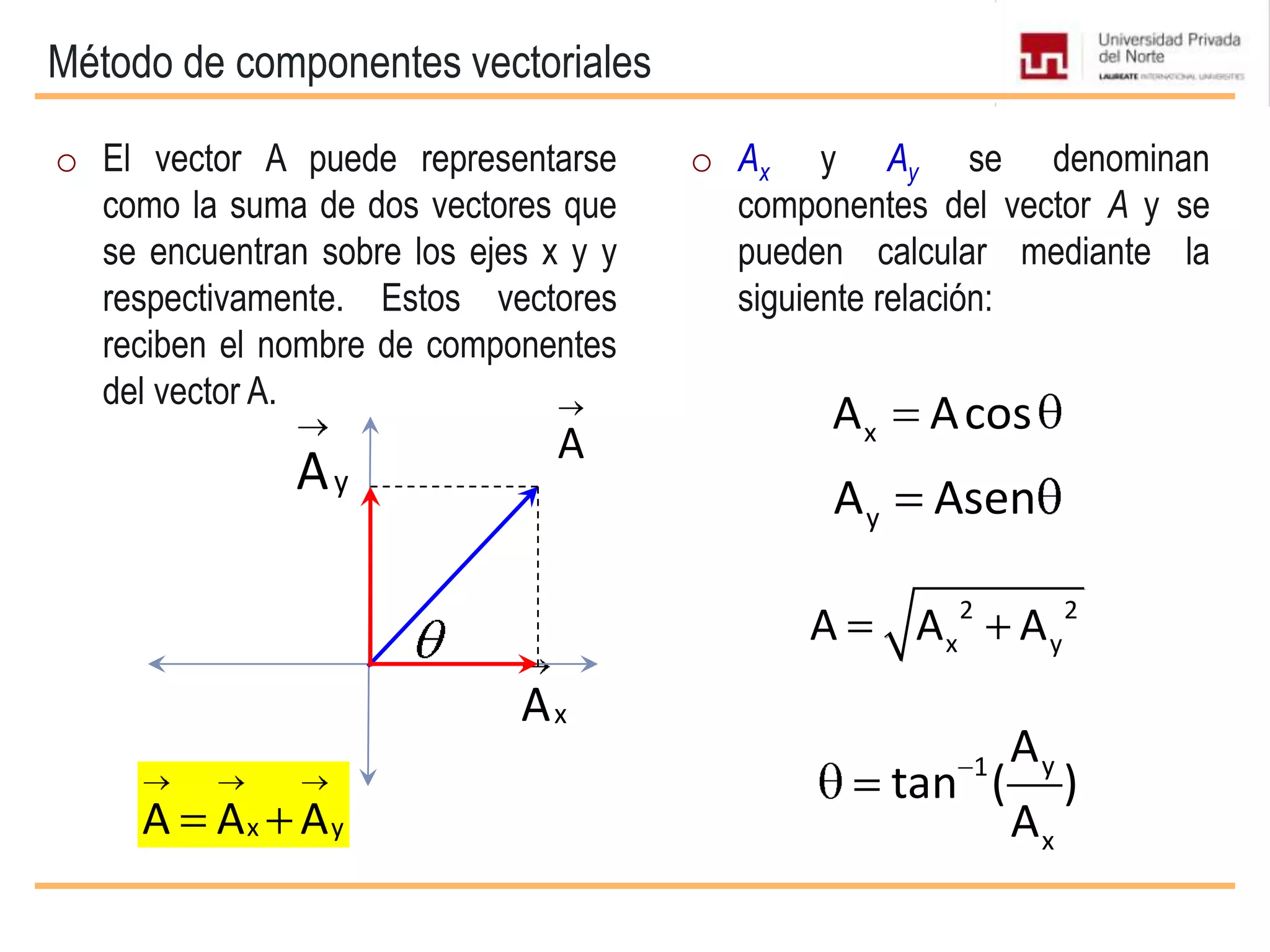
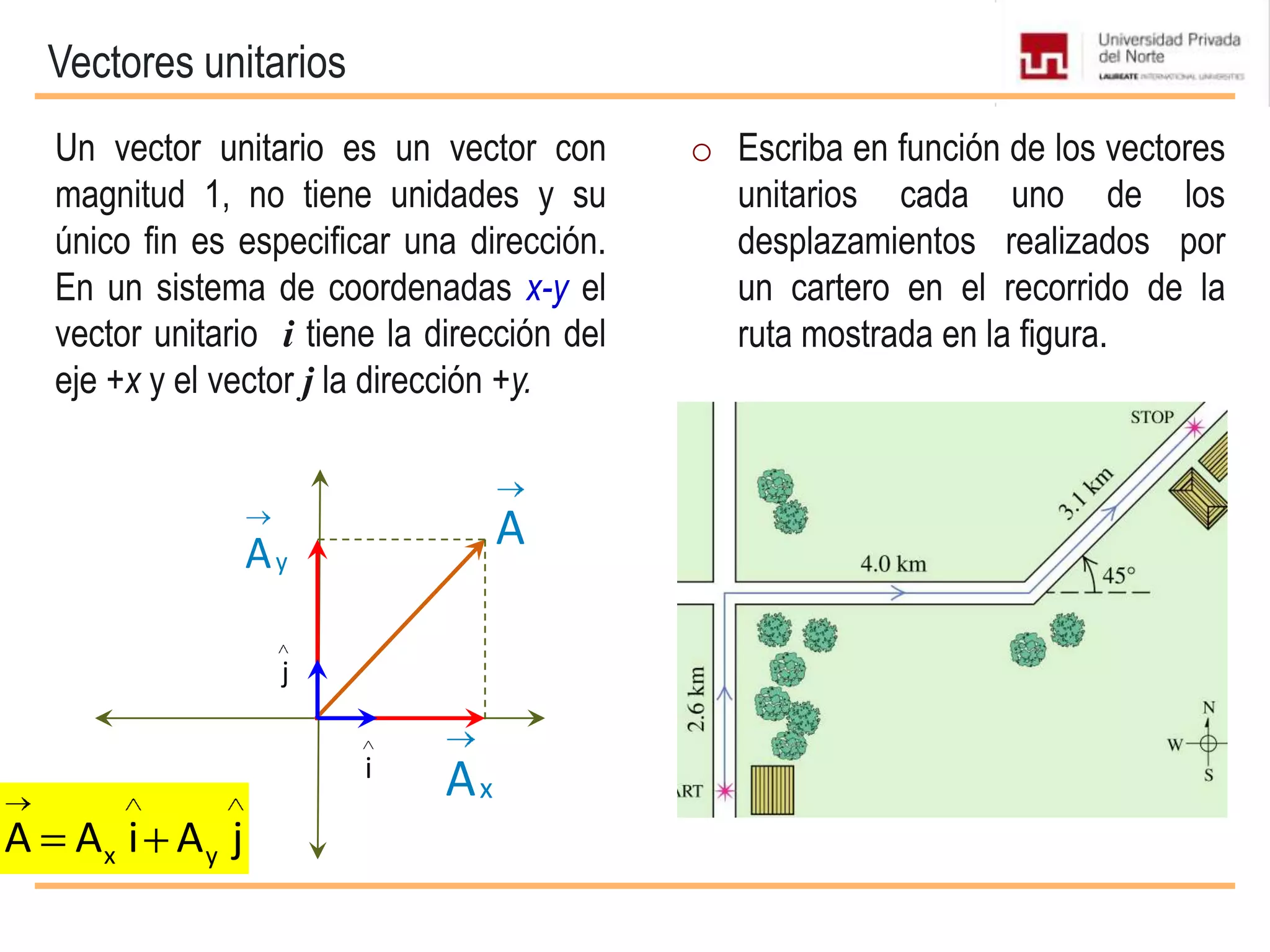
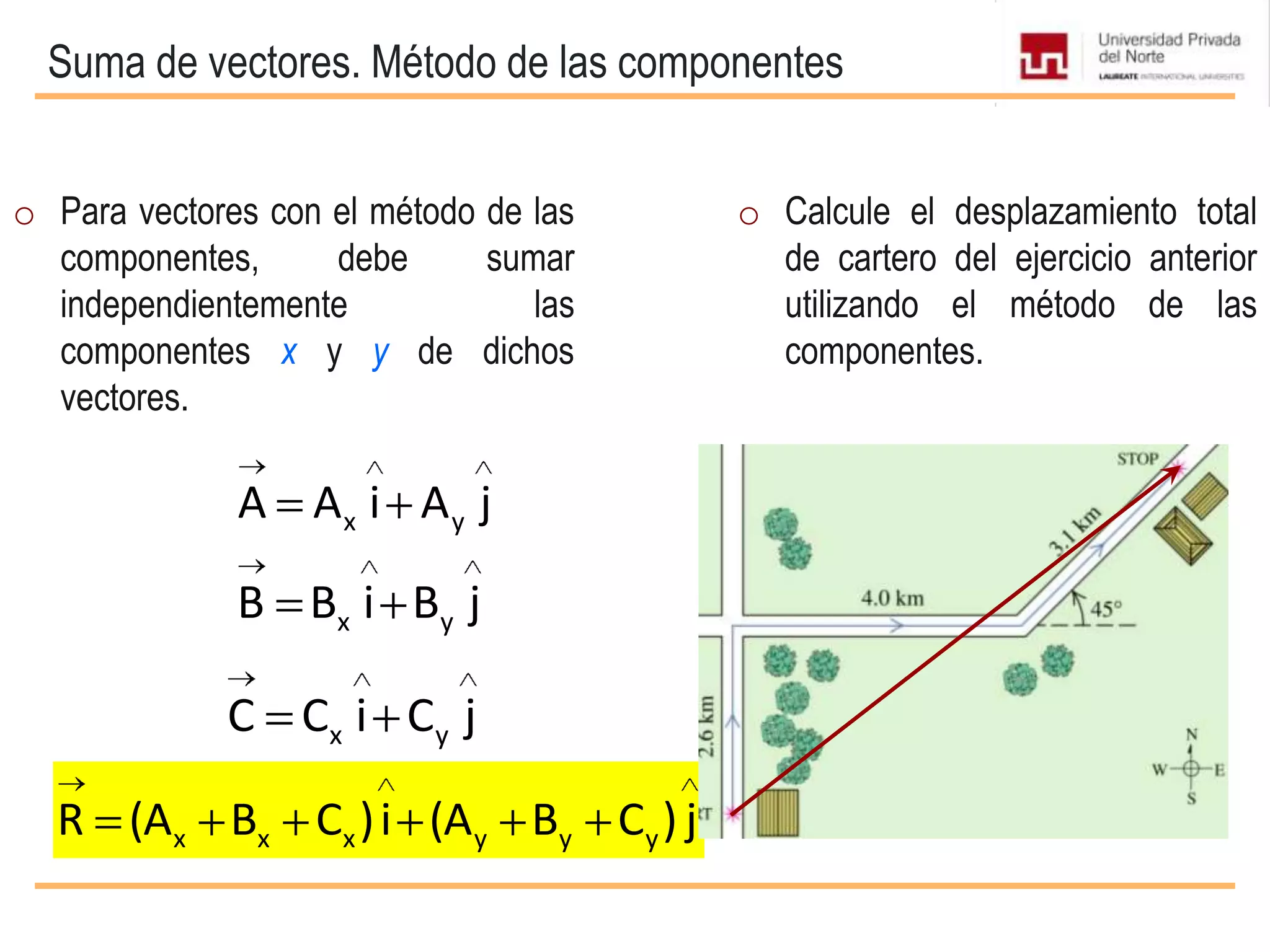
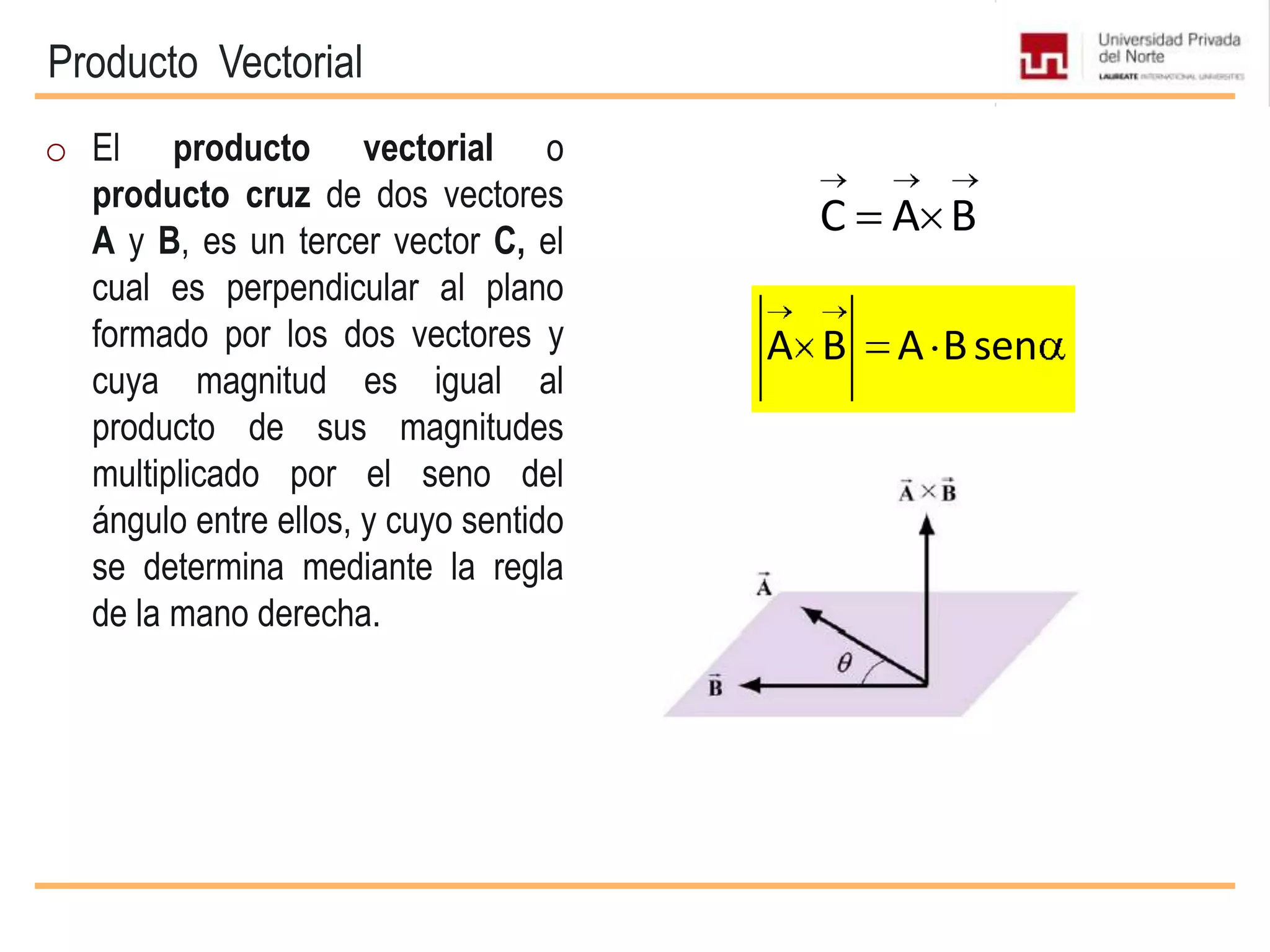
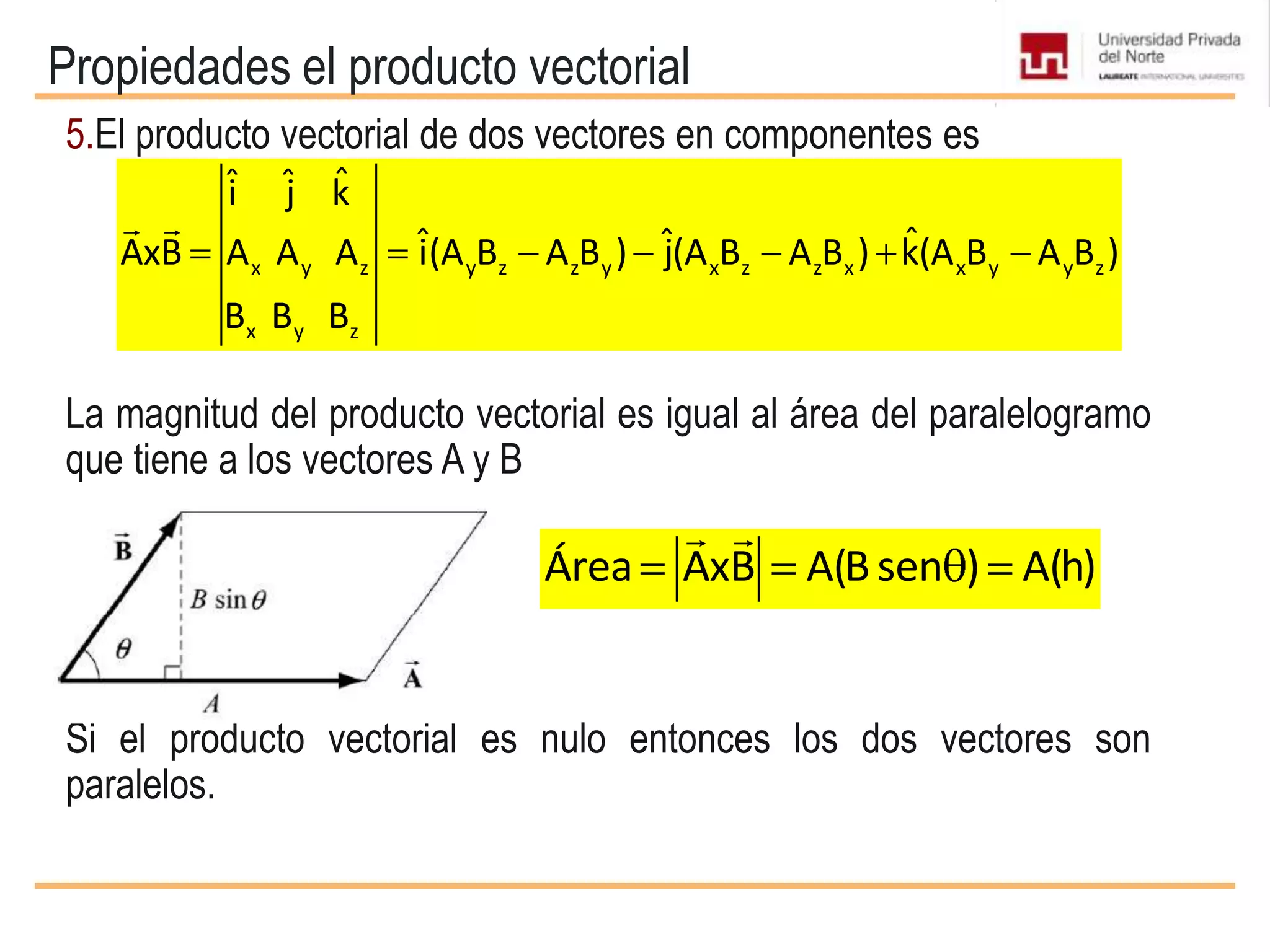
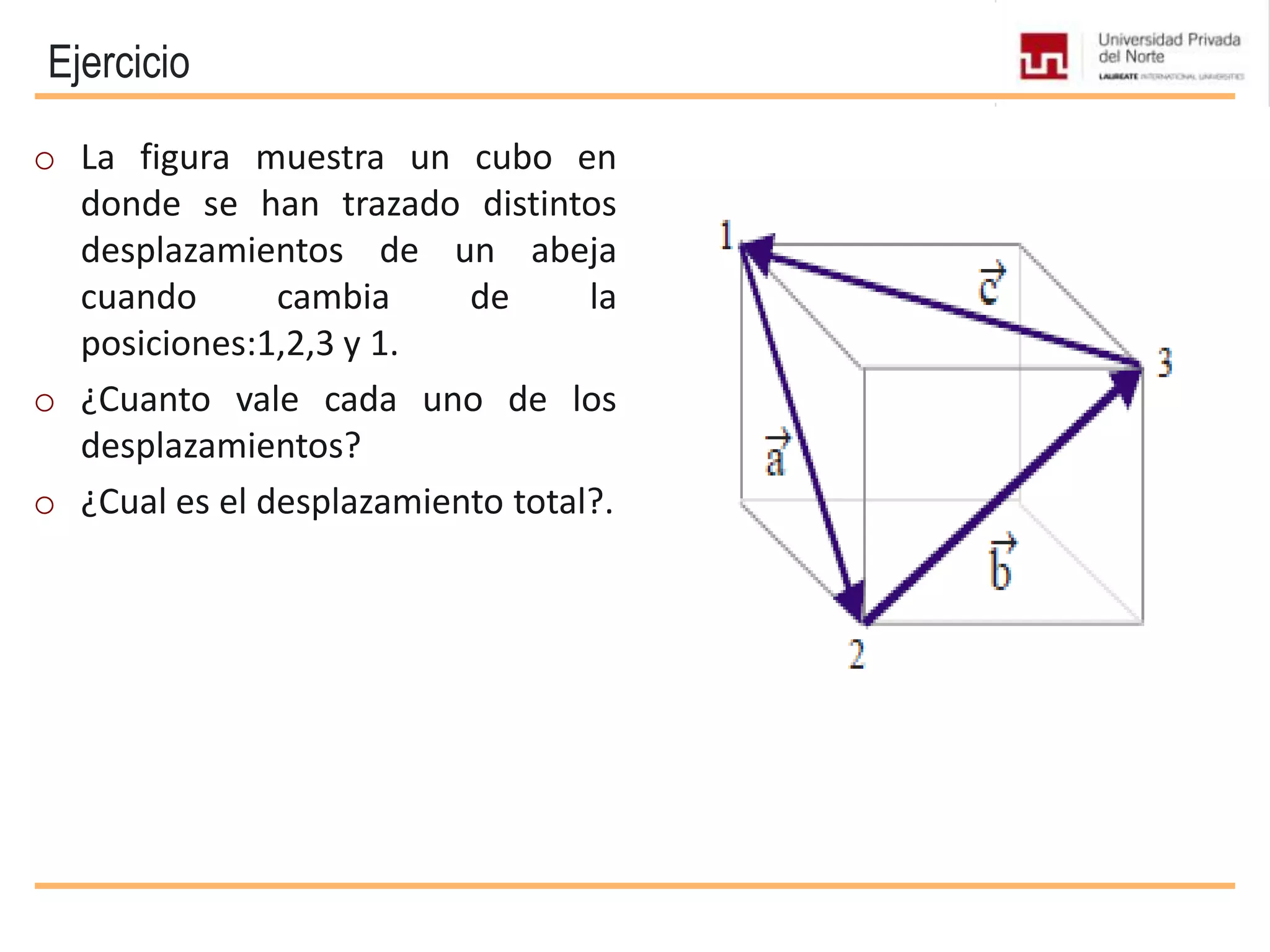
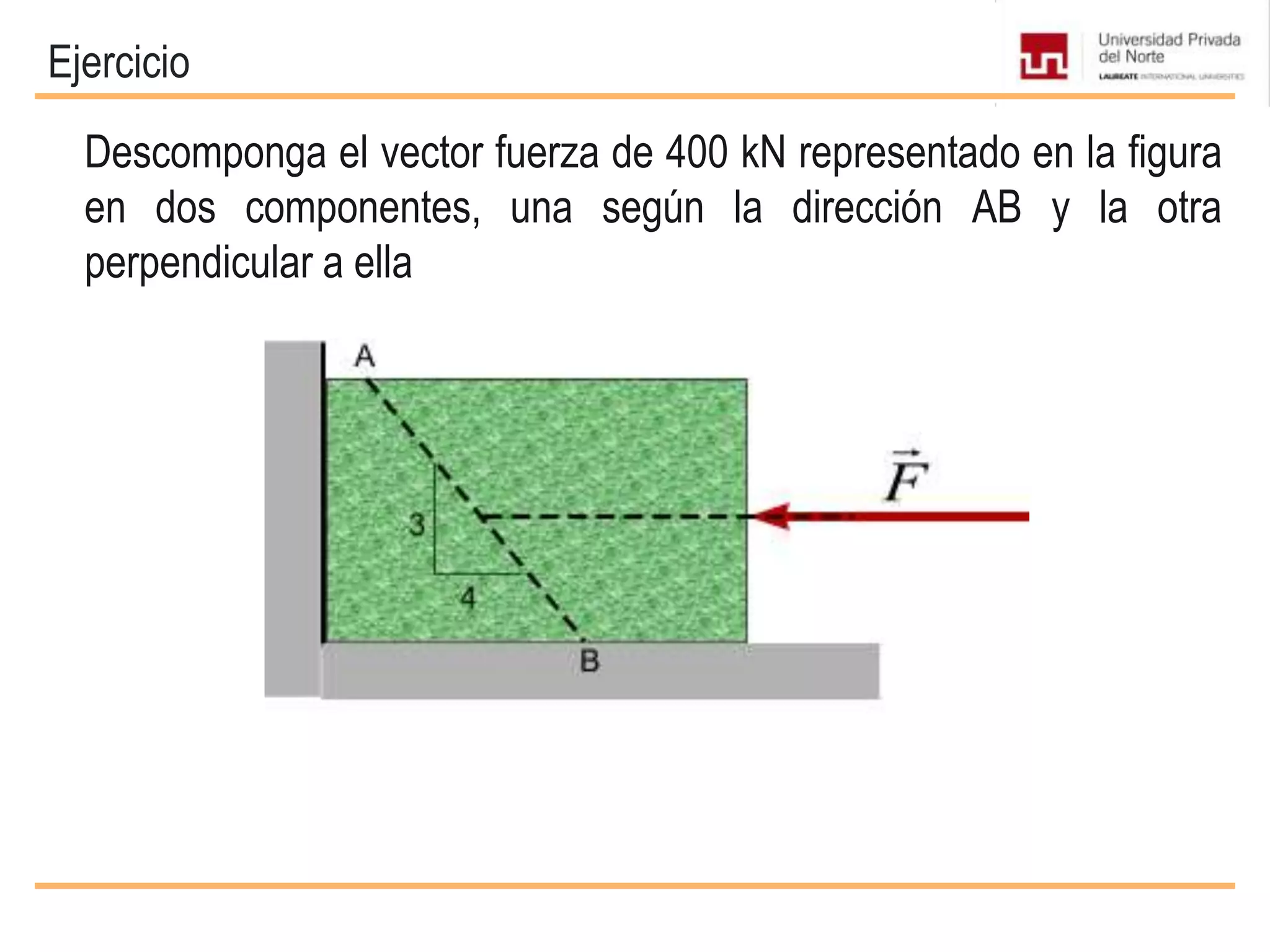
El documento presenta conceptos básicos sobre vectores, incluyendo definiciones de magnitudes escalares y vectoriales, métodos para representar y sumar vectores, y operaciones entre vectores como el producto escalar y vectorial. Se explican propiedades de estas operaciones y se incluyen ejemplos de su aplicación en problemas de mecánica.

1. Facultad de Ingeniería y Arquitectura
Semana 1
Vectores
Sílabo. Definición. Métodos de composición vectorial:
método del polígono, de las componentes.
MECÁNICA, OSCILACIONES Y ONDAS
Yuri Milachay Vicente
yur@upnorte.edu.pe

2. Magnitudes Físicas
Magnitud Física
o Se denominan magnitudes
físicas a las propiedades de los
cuerpos que son susceptibles a
ser medidas. Por ejemplo, la
longitud, la masa y el volumen
son magnitudes físicas ya que
siempre se pueden medir y
expresar a través de números:
5,0 metros, 2,0 kilogramos, 6,0
metros cúbicos.
5 kgmasa

3. Magnitudes escalares
o Son aquellas magnitudes
físicas que quedan totalmente
descritas mediante un número
y una unidad.
o Las operaciones con
magnitudes escalares se
realizan siguiendo las reglas de
las operaciones con números
reales.
200 g
300 g
500 g

4. Magnitudes vectoriales
• Existen magnitudes físicas, como la fuerza, que para quedar
definidas requiere conocerse el valor, la unidad y la dirección. A
estas las magnitudes se les denomina vectoriales.
La fuerza F produce un movimiento
hacia adelante
La fuerza F produce un movimiento
hacia atrás
F F

5. Representación de un vector
60
o La longitud de la flecha indica el valor de la magnitud física y su
orientación es su dirección.
origen
F
dirección
F 30N

6. Vectores iguales y Vectores opuestos
o Dos vectores son iguales si tienen
el mismo módulo y la misma
dirección.
o Dos vectores son opuestos si
tienen el mismo módulo pero
direcciones opuestas.
A B
180
A
B A
A B

7. Suma de vectores. Método gráfico
R
o Para sumar vectores con el
método gráfico, se unen de
manera consecutiva la punta de
un vector con la cola del
siguiente. La resultante se
obtiene uniendo la cola del
primer vector con la punta del
último.
A
B
A B R
R
B A R
Esta operación es conmutativa;
es decir, puede cambiarse el
orden de los vectores que se
están sumando y la resultante
será la misma.

8. Método de componentes vectoriales
A
xA
o El vector A puede representarse
como la suma de dos vectores que
se encuentran sobre los ejes x y y
respectivamente. Estos vectores
reciben el nombre de componentes
del vector A.
o Ax y Ay se denominan
componentes del vector A y se
pueden calcular mediante la
siguiente relación:
yA
x yA A A
xA Acos
yA Asen
2 2
x yA A A
y1
x
A
tan ( )
A

9. Un vector unitario es un vector con
magnitud 1, no tiene unidades y su
único fin es especificar una dirección.
En un sistema de coordenadas x-y el
vector unitario i tiene la dirección del
eje +x y el vector j la dirección +y.
Vectores unitarios
j
i
o Escriba en función de los vectores
unitarios cada uno de los
desplazamientos realizados por
un cartero en el recorrido de la
ruta mostrada en la figura.
x yA A i A j
A
xA
yA

10. Suma de vectores. Método de las componentes
x yA A i A j
x yB B i B j
o Para vectores con el método de las
componentes, debe sumar
independientemente las
componentes x y y de dichos
vectores.
o Calcule el desplazamiento total
de cartero del ejercicio anterior
utilizando el método de las
componentes.
x yC C i C j
x x x y y yR (A B C )i (A B C ) j

11. Ejercicios
o Calcule la resultante de los
vectores A y B mostrados en la
figura.
o Calcule la resultante de los
vectores A y B mostrados en la
figura.

12. Ejercicio
El vector A tiene componentes Ax =
1,30 cm, Ay = 2,55 cm; el vector B
tiene componentes Bx = 4,10 cm, By
= - 3,75 cm. Calcule:
a) Las componentes de la resultante
A+B
b) La magnitud y dirección de B-A
2 2
A B (5,40cm) ( 1,20cm)
 
A B 5,53cm
 
ˆ ˆB A (2,80cm)i ( 6,30cm)j
 
2 2
B A (2,80cm) ( 6,30cm)
 
1 1,20cm
tan 12,5º
5,40cm
B A 6,89cm
 

13. Producto Escalar
A B A Bcos
El producto escalar o producto
punto de dos vectores A y B
denotado por A.B y expresado
como «A multiplicado escalarmente
con B», se define como el producto
de los módulos de los vectores A y
B por el coseno del ángulo que
forman ellos.
A

B


14. Interpretación geométrica del producto escalar
Geométricamente, se muestra la disposición de los vectores en el
producto escalar en la figura.
B
Bcos
A A
B
Acos

15. Propiedades del producto escalar
x y zB B i B j B k
x y zA A i A j A k
o Producto escalar de dos vectores
en forma de componentes
o Si el producto escalar de dos
vectores es nulo. Entonces
dichos vectores son
perpendiculares.
o Producto escalar de vectores
unitarios.
A.B 0 A B
   
x x y y z zA B A B A B A B
i j 0 i i 0

16. Vector Proyección Ortogonal
A
eProyA A cos e
o Un vector proyección de A en las
dirección e es el vector cuya
magnitud es la componente
escalar de A en dicha dirección
A.e=A cosθ, y que está orientado
en la dirección de e.
θ

17. Producto Vectorial
C A B
A B A Bsen
o El producto vectorial o
producto cruz de dos vectores
A y B, es un tercer vector C, el
cual es perpendicular al plano
formado por los dos vectores y
cuya magnitud es igual al
producto de sus magnitudes
multiplicado por el seno del
ángulo entre ellos, y cuyo sentido
se determina mediante la regla
de la mano derecha.

18. Propiedades del producto vectorial
A B B A
A B C A C B C
El producto vectorial no es conmutativo
El producto vectorial es distributivo
Multiplicación de un escalar por el
producto vectorial.
Multiplicación vectorial de vectores
unitarios
A B C A B A C
cA B c A B

19. Propiedades el producto vectorial
5.El producto vectorial de dos vectores en componentes es
La magnitud del producto vectorial es igual al área del paralelogramo
que tiene a los vectores A y B
Si el producto vectorial es nulo entonces los dos vectores son
paralelos.
x y z y z z y x z z x x y y z
x y z
ˆˆ ˆi j k
ˆˆ ˆAxB A A A i(A B A B ) j(A B A B ) k(A B A B )
B B B
 
Área AxB A(Bsen ) A(h)
 

20. Ejercicio
o La figura muestra un cubo en
donde se han trazado distintos
desplazamientos de un abeja
cuando cambia de la
posiciones:1,2,3 y 1.
o ¿Cuanto vale cada uno de los
desplazamientos?
o ¿Cual es el desplazamiento total?.

21. Ejercicio
Descomponga el vector fuerza de 400 kN representado en la figura
en dos componentes, una según la dirección AB y la otra
perpendicular a ella

22. Ejercicio
La resultante de la tres fuerzas mostradas en la figura es vertical.
Determine: (a) la magnitud de la fuerza A y (b) la resultante del
sistema

23. Ejercicio
Determine la resultante del sistema de vectores fuerza mostrados
en la figura