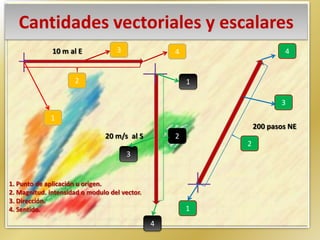
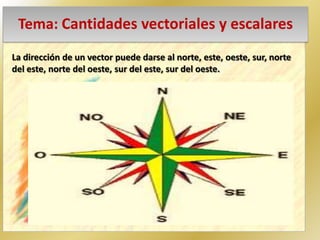
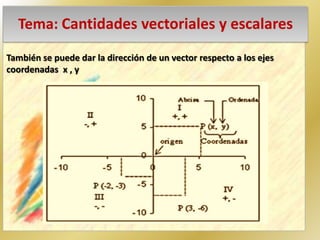
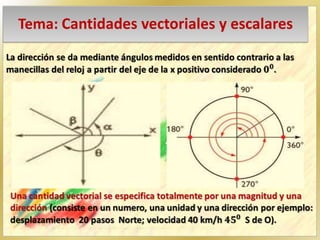
1. El documento describe las diferencias entre cantidades vectoriales y escalares. Las cantidades vectoriales como la fuerza requieren una dirección y sentido, mientras que las cantidades escalares solo necesitan un valor numérico. 2. Se explican las características de un vector, incluyendo magnitud, dirección y sentido. 3. También se describen métodos gráficos como el triángulo, paralelogramo y polígono para sumar vectores.