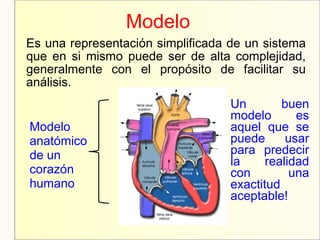
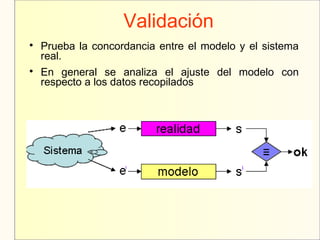
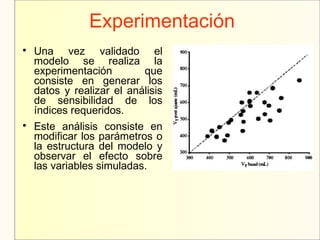
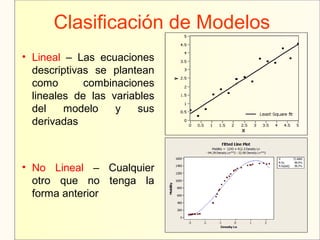
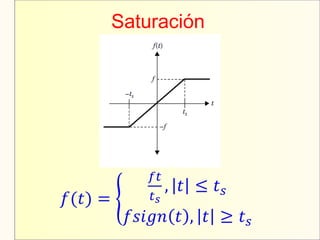
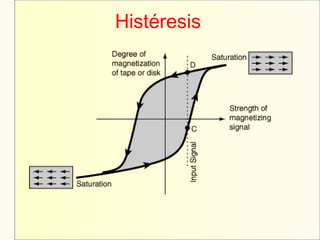
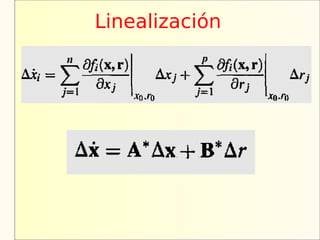
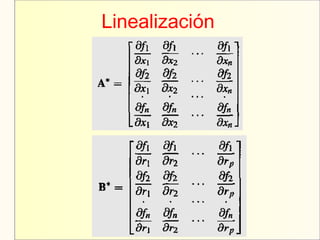
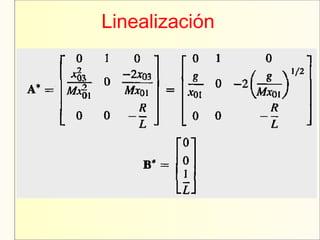
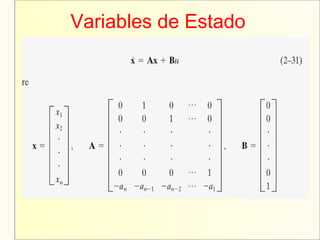
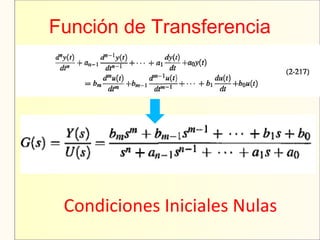
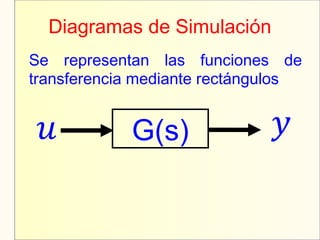
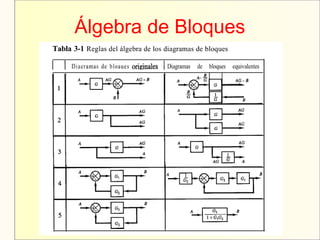
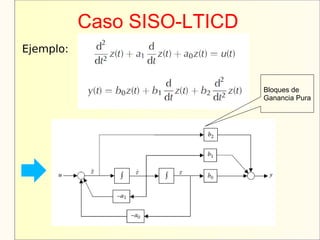
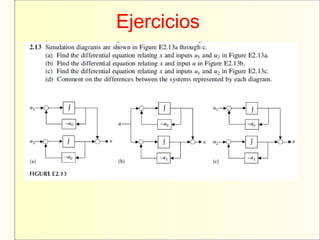
El documento aborda el modelaje y simulación de sistemas dinámicos, presentando conceptos fundamentales, tipos de modelos y etapas clave en un proyecto de simulación. Se discuten metodologías de validación, experimentación y análisis de resultados, así como herramientas de software para la simulación. También se presenta una clasificación de modelos basados en características específicas y se mencionan aspectos prácticos como la toma de decisiones y la comunicación con los clientes.