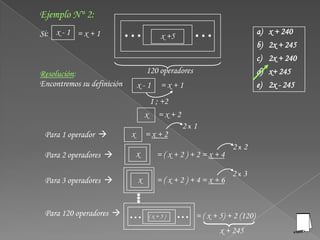
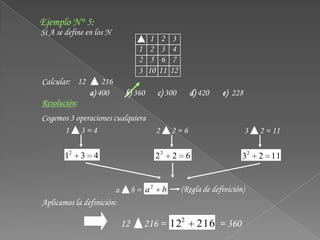
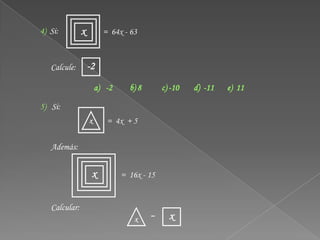
El documento explica las operaciones matemáticas y los operadores matemáticos. Define una operación matemática como un proceso que transforma una o más cantidades en un resultado bajo ciertas reglas. Los operadores matemáticos, como +, -, *, /, representan las operaciones y permiten reconocer la regla a aplicar. El documento provee varios ejemplos para ilustrar cómo aplicar diferentes definiciones de operaciones implícitas.

2. OPERACIONES MATEMÁTICOS
¿Qué es una Operación Matemática?
Es un proceso que consiste en la transformación de una o
más cantidades en una cantidad llamada resultado, bajo
ciertas reglas o condiciones en la cual define la operación.
Tosa operación matemática presenta una regla de definición
y un símbolo que la identifica llamado OPERADOR
MATEMÁTICO.
a b adición a b división
a b sustracció n a2 potenciaci
ón
a.b multiplica
ción a radicación

3. ¿Qué es un Operador Matemático?
Es aquel símbolo que representa a una operación matemática. Nos permite
reconocer la operación matemática a emplear con su respectiva regla de
definición. 2
a *b 2a 3b
Ejemplo N° 1: Operador matemático Regla de
Definimos en N definición
xy y x = 18y – 11x
Calcular: A=(1 2) (8 9) a) -19
Resolución:
b) 19
Dándole forma a los datos numéricos obtenemos:
(1 2) = 1 2 21 = 18 ( 2 ) – 11 ( 1 ) = 25 c) -18
(8 9) = 2 3 32 = 18 ( 3 ) – 11 ( 2 ) = 32 d) F.D.
Reemplazamos: A = ( 1 2) (8 9) e) N.A.
A = 25 32
A = 52 2 5 = 18 ( 2 ) – 11 ( 5 )
36 – 55 = -19

4. Ejemplo N° 2:
Si: x - 1 = x + 1 a) x + 240
x +5
b) 2x + 245
c) 2x + 240
Resolución: 120 operadores d) x+ 245
Encontremos su definición x-1 =x+1 e) 2x - 245
1 ; +2
x =x+2
2x1
Para 1 operador  x =x+2
2x2
Para 2 operadores  x =(x+2)+2=x+4
2x3
Para 3 operadores  x =(x+2)+4=x+6
Para 120 operadores  (x+5) = ( x + 5) + 2 (120)
x + 245

5. Ejemplo N° 3: a) 1
Si: a * b = a 2 ab 1 b) 2
c) 3
Calcular: d) 4
e) 5
A=3*(3*(3*(3*…))))
A
Resolución:
A = 3 * A  Aplicamos la definición
A = 32 - 3A - 1
A + 3A= 9 - 1
4A= 8
A= 2

6. Ejemplo N° 4:
Dado: 23 * 42 = 16
35 * 16 = 23
64 * 71 = 34
a) 96 b) 102 c) 105 d) 98 e ) 100
Resolución:
23 * 42 = 2 x 2 + 3 x 4 = 16
35 * 16 = 3 x 6 + 5 x 1 = 23
64 * 71 = 6 x 1 + 4 x 7 = 34
59 * 86 = ( 5 ) ( 6 ) + ( 9 ) ( 8 ) = 102

7. Ejemplo N° 5:
Si A se define en los N
1 2 3
1 2 3 4
2 5 6 7
3 10 11 12
Calcular: 12 216
a) 400 b) 360 c) 300 d) 420 e) 228
Resolución:
Cogemos 3 operaciones cualquiera
1 3=4 2 2=6 3 2 = 11
12 3 4 22 2 6 32 2 11
a b = a2 b (Regla de definición)
Aplicamos la definición:
12 216 = 122 216 = 360

8. Oración Implícita:
m*n R 0
m*n m(n * m) 2
Calcule: 8 * 1
Resolución:
Si reemplazamos, tendremos: 8 * 1 = 8 ( 1 * 8 ) 2 y tenemos que calcular ( 1 * 8 )
( 1 * 8 ) = 1 ( 8 * 1 ) 2  tendremos un círculo de lo mismo
Debemos encontrar la definición
m*n =m(n*m)2
n* m = n ( m * n ) 2  por definición
2
m * n m n(m * n) 2
m * n = m n 2( m* n ) 4
1 = m n 2( m * n ) 3
1
m*n  Regla por definición
m n2
1 1 1
8 *1 3 3
8(1) 2 8 2

9. Para el Alumno:
1) Se define, en R la operación: (b * a) 2
a *b
4
Calcule: 3 * 5
a) 4 b) 3 c) 6 d) 7 e) 8
2) Se tiene:
72 10 = 56
48 15 = 54
100 1 = 52
Calcule: 12 40
a) 80 b) 86 c) 90 d) 92 e) 72
3) Se define, el operador de la siguiente forma:
m = (m + 1 ) 3
x = 8
a) 2 b) 1 c) 3 d) -1 e) 0

10. 4) Si: x = 64x - 63
Calcule: -2
a) -2 b) 8 c) -10 d) -11 e) 11
5) Si:
x = 4x + 5
Además:
x = 16x - 15
Calcular:
x - x