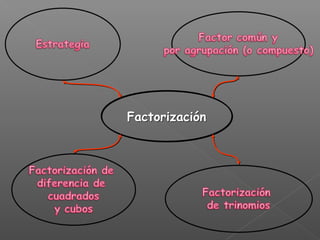
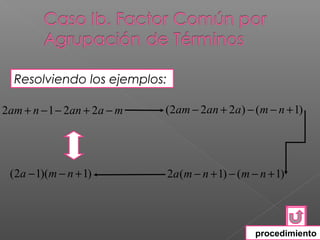
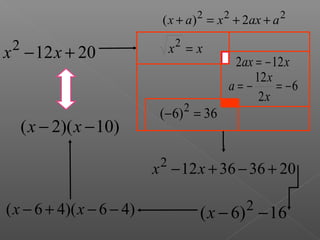
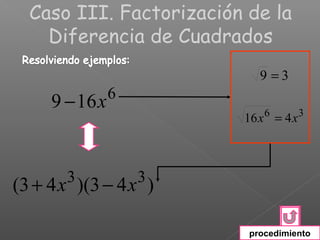
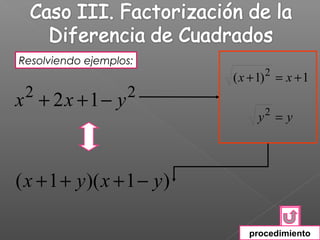
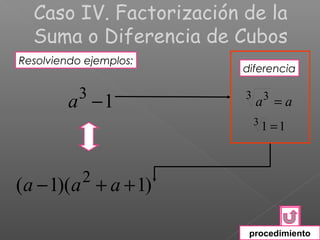
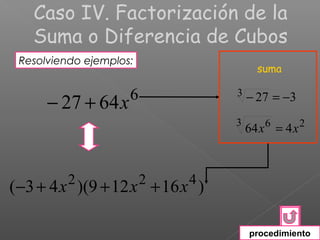
El documento explica los diferentes métodos para factorizar expresiones algebraicas: 1) Factorizar factores comunes, 2) Agrupar términos o usar fórmulas para trinomios cuadrados perfectos y diferencias/sumas de cuadrados/cubos, 3) Asegurarse de que la expresión está completamente factorizada. Se proveen ejemplos resueltos para ilustrar cada método.

2. Factorización

3. ( a − b )( x − z ) ( a − b) y ( x − z)
a − b( x − z ) b y ( x − z)
Factorización
2 2
ma − mb = m(a + b)(a − b)

4. 2 2
ma − mb
2
3x y − x
2 2 2 4
24a xy − 36 x y
a ( x + 1) − b( x + 1)

5. Ejemplo Máx. Segundo Factorización
factor factor
común
ma − mb2 2 m 2
a −b 2 m( a 2 − b 2 )
2 3 xy − 1 x(3xy − 1)
3x y − x x
2 2
24a xy − 36 x y 2 4 12xy 2 2
2a − 3 xy 2 12 xy 2 (2a 2 − 3 xy 2 )
a ( x + 1) − b( x + 1) x +1 a −b ( x + 1)(a − b)

6. ax + a − bx − b
2
3m − 6mn + 4m − 8n
2am + n − 1 − 2an + 2a − m

7. Resolviendo los ejemplos:
ax + a − bx − b (ax + a ) − (bx + b)
(a − b)( x + 1) a ( x + 1) − b( x + 1)
procedimiento

8. Resolviendo los ejemplos:
2
3m − 6mn + 4m − 8n (3m 2 − 6mn) + (4m − 8n)
(3m + 4)(m − 2n) 3m(m − 2n) + 4(m − 2n)
procedimiento

9. Resolviendo los ejemplos:
2am + n − 1 − 2an + 2a − m (2am − 2an + 2a) − (m − n + 1)
(2a − 1)(m − n + 1) 2a (m − n + 1) − (m − n + 1)
procedimiento

10. 2 2
a + 2ab + b
2
x − 2x +1
2 2
4a x − 12ax + 9

11. Resolviendo ejemplos:
a2 = a
2 2
a + 2ab + b b2 = b
+ 2ab
( a + b) 2
procedimiento

12. Resolviendo ejemplos:
4a 2 x 2 = 2ax
¿ es tcp ?
2 2 9 =3
4a x − 12ax + 9 Sí
− 12ax
2
(2ax − 3)
procedimiento

13. 2
Trinomio de la forma x + cx + d
2
x − 12 x + 20
2 2
9a x − 39ax + 30

14. x2 = x
2
x − 12 x + 20 − 10 − 2 = −12
(−10)(−2) = 20
( x − 10)( x − 2)
procedimiento

15. Resolviendo ejemplos:
9a 2 x 2 = 3ax
2 2 − 10 − 3 = −13
9a x − 39ax + 30
(−10)(−3) = 30
(3ax − 3)(3ax − 10)
3(ax − 1)(3ax − 10) procedimiento

16. 2
x + cx + d
2
x − 12 x + 20
2 2
9a x − 39ax + 30

17. ( x + a) 2 = x 2 + 2ax + a 2
2
x − 12 x + 20 x2 = x
2ax = − 12 x
12 x
a=− = −6
2x
2
(− 6) = 36
( x − 2)( x − 10)
2
x − 12 x + 36 − 36 + 20
( x − 6 + 4)( x − 6 − 4) 2
( x − 6) − 16

18. Resultado del siguiente producto notable:
2 2 2
( a + b) = a + 2ab + b
o,
2
( a − b) 2
= a − 2ab + b 2

19. 2
x + cx + d
Resultado del siguiente producto notable:
2
( x + a )( x + b) = x + (a + b) x + ab
Donde:
c = a+b y d = ab

20. 2 2
a −b
2
a −1
6
9 − 16 x
2 2
x + 2x +1− y

21. Caso III. Factorización de la
Diferencia de Cuadrados
9 =3
6
9 − 16 x
16 x 6 = 4 x 3
3 3
(3 + 4 x )(3 − 4 x )
procedimiento

22. Resolviendo ejemplos:
( x + 1) 2 = x + 1
2 2
x + 2x +1− y 2
y =y
( x + 1 + y )( x + 1 − y )
procedimiento

23. 3 3
a −b
3
a −1
6
27 + 64 x

24. Caso IV. Factorización de la
Suma o Diferencia de Cubos
Resolviendo ejemplos:
diferencia
3
a −1 3 3
a =a
3 1 =1
2
(a − 1)(a + a + 1)
procedimiento

25. Caso IV. Factorización de la
Suma o Diferencia de Cubos
Resolviendo ejemplos:
suma
6 3 − 27 = −3
− 27 + 64 x
3
64 x 6 = 4 x 2
2 2 4
(−3 + 4 x )(9 + 12 x + 16 x )
procedimiento

26. 2
(a + b)(a − b) = a − b 2

27. Resultado del siguiente producto notable:
2 2 3 3
(a + b)(a − ab + b ) = a + b
o bien,
2 2 3 3
(a − b)(a + ab + b ) = a −b

28. 1. Factorizar todos los factores comunes.
2. Observar el número de términos entre
paréntesis (o en la expresión original). Si
hay:
I. Cuatro términos: factorizar por agrupación.
II. Tres términos: probar si es TCP y factorizar
así; si no es TCP, emplear el caso general.
III. Dos términos y cuadrados: buscar la
diferencia de cuadrados y factorizarla.
IV. Dos términos y cubos: buscar la suma o
diferencia de cubos y factorizar.
3. Asegurarse de que la expresión está
factorizada completamente.