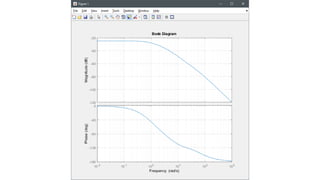
El documento presenta 5 ejemplos de construcción de diagramas de Bode para diferentes sistemas. En cada ejemplo se calculan los factores de cada término, se identifican las frecuencias de corte y las pendientes, y se grafican los diagramas asintóticos de magnitud y fase.

1. DIAGRAMAS DE BODE
EJEMPLOS

2. Ejemplo 1.
Construya los gráfico asintóticos de magnitud y fase de Bode para el
siguiente sistema:
G s =
4
0.5s + 3

3. Ejemplo 1.
Cálculos:
G s =
4
0.5s + 3
→
4
3
0.5
3
s + 1
→
4
3
s
6
+ 1
, s = jω
G s =
4
3
×
1
s
6
+ 1
Factores:
•
4
3
→ 20 log
4
3
≈ 2.5 , ϕ = 0°
•
s
6
+ 1 → ωc = 6 , −20 log
ω
6
2
+ 1 , ϕ = − tan−1 ω
6
ȁωc
= −45°
este factor tiene unos -20 dB/dec.

4. Ejemplo 1. – Diagrama de magnitud [dB]
0
−10
−30
−20
+10
100
10−1
10−2
101 102
103
−20 dB/dec
−20 log
s
6
+ 1
ω

5. Ejemplo 1. – Diagrama de fase [grados]
0
−45
−180
−90
+45
100
10−1
10−2
101 102
103
ω

7. Ejemplo 2.
Construya el diagrama de Bode asintótico de magnitud y fase para el siguiente
sistema:
G s =
1
1 − s

8. Ejemplo 2.
Realizando los cálculos:
G jω =
1
1 − jω
Factores:
1
1−jω
→ −20 log 1 + ω2
ϕ = − tan−1
−
ω
1
, ω = ωc = 1 → − −45° = 45°

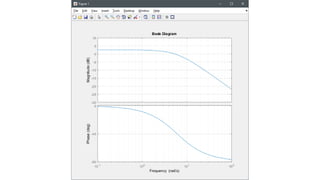
9. Ejemplo 2. – Diagrama de magnitud [dB]
0
−20
−60
−40
+20
100
10−1
10−2
101 102
103
−20 dB/dec
ω

10. Ejemplo 2. – Diagrama de fase [grados]
+90
+45
−45
0
+135
100
10−1
10−2
101 102
103
ω

12. Ejemplo 3.
Construya el diagrama de Bode asintótico de magnitud y fase para el siguiente
sistema:
G s =
11.27
s2 + 4s + 4
Calcule el coeficiente de amortiguamiento y la ganancia cuando la frecuencia de
muestreo es igual a la frecuencia de corte e indique si es sistema es sub-
amortiguado, críticamente amortiguado o sobre-amortiguado.

13. Ejemplo 3.
Realizando los cálculos:
G s =
11.27
s2 + 4s + 4
→
11.27
4
×
1
s
2
2
+ s + 1
→
11.27
4
×
1
jω
2
2
+ jω + 1
Factores:
•
11.27
4
→ AG = 20 log 11.27/4 ≅ 9
•
1
jω
2
2
+jω+1
→ ωC = 2 , AG = −
40dB
dec
, ϕ = −90° , AGωc
= 9 − 20 × log 2 × 1 = 2.98 dB
2ζωn = 4 → ζ = 1
Es críticamente amortiguado.
2

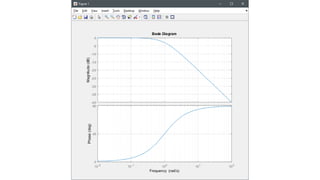
14. Ejemplo 3. – Diagrama de magnitud [dB]
0
−20
−60
−40
+20
100
10−1
10−2
101 102
103
ω
2

15. Ejemplo 3. – Diagrama de fase [grados]
−45
−90
−180
−135
+0
100
10−1
10−2
101 102
103
ω

17. Ejemplo 4.
Construya el diagrama de Bode asintótico de magnitud y fase para el siguiente
sistema:
G s =
10 s + 3
s s + 2 s2 + s + 2

18. Ejemplo 4.
Realizando los cálculos:
10 s + 3
s s + 2 s2 + s + 2
→
10 × 3
2 × 2
s
3 + 1
s
s
2
+ 1
s
2
2
+
s
2
+ 1
Factores:
•
10×3
2×2
→ 20 log 7.5 ≅ 17.5
•
s
3
+ 1 → ωc = 3 , +20
dB
dec
, ϕȁωc
= +45°
•
1
s
→ −20
dB
dec
, ϕ = −45°
•
1
s
2
+1
→ ωc = 2, −20
dB
dec
, ϕ = −45°
•
1
s
2
2
+
s
2
+1
, ωc = 2 , −40
dB
dec
, ϕ = −90°

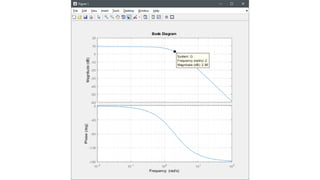
19. Ejemplo 4. – Diagrama de magnitud [dB]
20
0
−80
−20
40
100
10−1
10−2
101 102
103
ω
60
80
−40
−60

20. Ejemplo 4. – Diagrama de fase [grados]
−90
100
10−1
10−2
101 102
103
ω
−45
0
−180
−135
−270
−225
−360
−315
45
90

22. Ejemplo 5.
Construya el diagrama de Bode asintótico de magnitud y fase para el siguiente
sistema:
G s =
(s + 20)
s + 1 s + 7 s + 50

23. Ejemplo 5.
Realizando los cálculos:
(s + 20)
s + 1 s + 7 s + 50
→
20
7 × 50
s
20 + 1
s
1
+ 1
s
7
+ 1
s
50
+ 1
factores frec. de corte dB/dec ° ቚ
ω=ωc
20
7 × 50
no hay 0, −25 cte 0
s
20
+ 1 20 +20 +45
s
1
+ 1 1 −20 −45
s
7
+ 1 7 −20 −45
s
50
+ 1 50 −20 −45

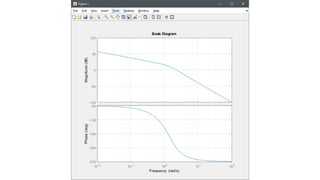
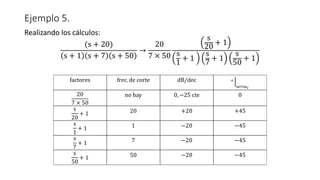
24. Ejemplo 5. – Diagrama de magnitud [dB]
0
−80
−20
100
10−1
10−2
101 102
103
ω
−40
−60
−160
−100
−120
−140

25. Ejemplo 5. – Diagrama de fase [grados]
−90
100
10−1
10−2
101 102
103
ω
−45
0
−180
−135
−270
−225
−360
−315
45
90