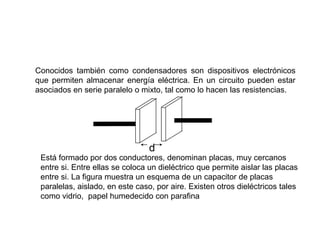
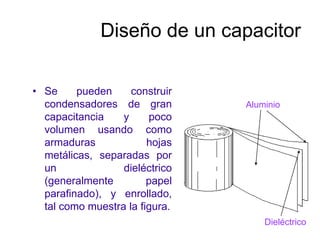
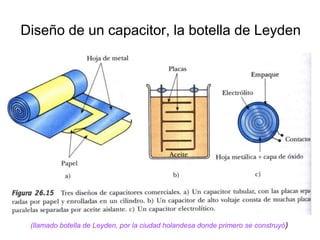
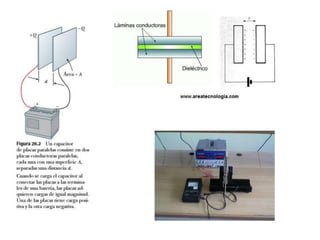
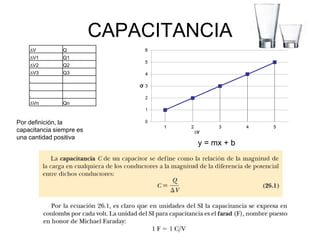
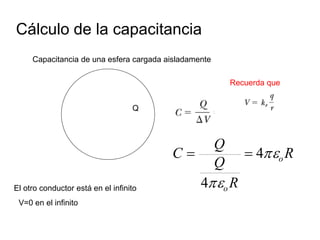
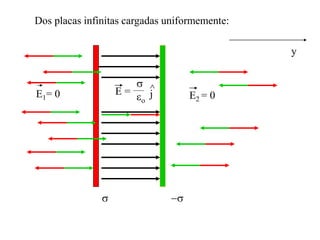
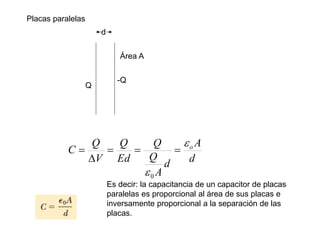
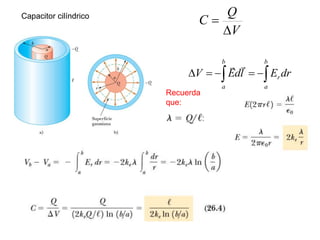
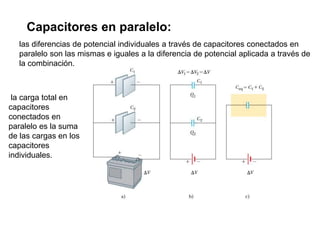
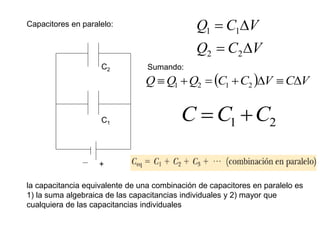
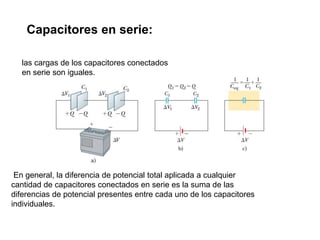
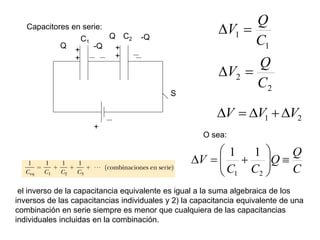
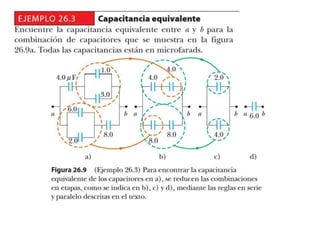
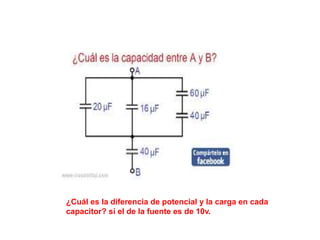
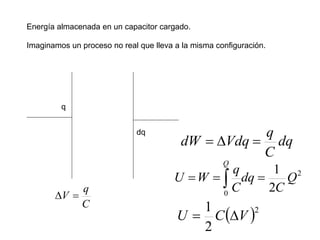
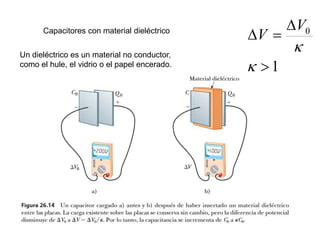
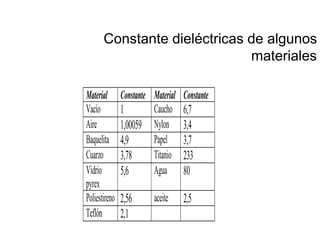
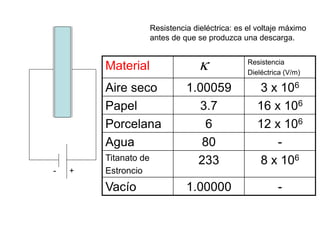
El documento describe los capacitores, su capacitancia y los dieléctricos. Un capacitor está formado por dos placas conductoras separadas por un dieléctrico y puede almacenar energía eléctrica. La capacitancia depende del área, distancia entre placas y material dieléctrico. Los capacitores se pueden conectar en serie o paralelo para variar su capacitancia equivalente.

1. CAPACITORES,
CAPACITANCIA Y
DIELECTRICOS.

2. • El capacitor es uno de los tres elementos simples de circuitos que
se interconectan mediante alambres para formar un circuito
eléctrico.
• Definición: es un dispositivo eléctrico “pasivo” el cual debido a una
diferencia de potencial (fuente) almacena carga (como energía)
debido a la presencia de un campo eléctrico.

3. Conocidos también como condensadores son dispositivos electrónicos
que permiten almacenar energía eléctrica. En un circuito pueden estar
asociados en serie paralelo o mixto, tal como lo hacen las resistencias.
Está formado por dos conductores, denominan placas, muy cercanos
entre si. Entre ellas se coloca un dieléctrico que permite aislar las placas
entre si. La figura muestra un esquema de un capacitor de placas
paralelas, aislado, en este caso, por aire. Existen otros dieléctricos tales
como vidrio, papel humedecido con parafina
d

4. Diseño de un capacitor
• Se pueden construir
condensadores de gran
capacitancia y poco
volumen usando como
armaduras hojas
metálicas, separadas por
un dieléctrico
(generalmente papel
parafinado), y enrollado,
tal como muestra la figura.
Aluminio
Dieléctrico

5. Diseño de un capacitor, la botella de Leyden
• Es un condensador
cilíndrico, tiene por
armaduras hojas metálicas
que envuelven el recipiente
de vidrio (dieléctrico) por
fuera y por dentro.
• Ocupa un volumen grande y
tiene relativamente poca
capacidad.
Vidrio
Hojas
metálicas
(llamado botella de Leyden, por la ciudad holandesa donde primero se construyó)

7. CAPACITANCIA
∆V Q
∆V1 Q1
∆V2 Q2
∆V3 Q3
.
.
.
∆Vn Qn
y = mx + b
Por definición, la
capacitancia siempre es
una cantidad positiva

9. Cálculo de la capacitancia
R
R
Q
Q
C o
o


4
4


V=0 en el infinito
Q
El otro conductor está en el infinito
Capacitancia de una esfera cargada aisladamente
Recuerda que

10. Dos placas infinitas cargadas uniformemente:
s -s
E1= 0
y
E = ^
E2 = 0
s
o
j

11. Placas paralelas
d
Área A
d
A
d
A
Q
Q
Ed
Q
V
Q
C o







0
Q
-Q
Es decir: la capacitancia de un capacitor de placas
paralelas es proporcional al área de sus placas e
inversamente proporcional a la separación de las
placas.

13. Capacitor cilíndrico
V
Q
C


dr
E
l
d
E
V
b
a
r
b
a

 -

-




Recuerda
que:

14. Capacitor esférico:
Recuerda
que:

15. Combinaciones de capacitores
En los circuitos eléctricos con
frecuencia se combinan dos o más
capacitores. Es posible calcular la
capacitancia equivalente de ciertas
combinaciones utilizando los
métodos descritos en esta sección,
en donde supondrá que los
capacitores a combinar están
inicialmente descargados.

16. las diferencias de potencial individuales a través de capacitores conectados en
paralelo son las mismas e iguales a la diferencia de potencial aplicada a través de
la combinación.
Capacitores en paralelo:
la carga total en
capacitores
conectados en
paralelo es la suma
de las cargas en los
capacitores
individuales.

17. Capacitores en paralelo:
+
C1
C2
V
C
Q
V
C
Q




2
2
1
1
Sumando:
  V
C
V
C
C
Q
Q
Q 





 2
1
2
1
2
1 C
C
C 

la capacitancia equivalente de una combinación de capacitores en paralelo es
1) la suma algebraica de las capacitancias individuales y 2) mayor que
cualquiera de las capacitancias individuales

18. las cargas de los capacitores conectados
en serie son iguales.
Capacitores en serie:
En general, la diferencia de potencial total aplicada a cualquier
cantidad de capacitores conectados en serie es la suma de las
diferencias de potencial presentes entre cada uno de los capacitores
individuales.

19. Capacitores en serie:
Q -Q
Q -Q
+
S
+
+
+
+
C1
C2
2
2
1
1
C
Q
V
C
Q
V




2
1 V
V
V 




O sea:
C
Q
Q
C
C
V 











2
1
1
1
el inverso de la capacitancia equivalente es igual a la suma algebraica de los
inversos de las capacitancias individuales y 2) la capacitancia equivalente de una
combinación en serie siempre es menor que cualquiera de las capacitancias
individuales incluidas en la combinación.

22. ¿Cuál es la diferencia de potencial y la carga en cada
capacitor? si el de la fuente es de 10v.

23. Energía almacenada en un capacitor cargado.
Imaginamos un proceso no real que lleva a la misma configuración.
dq
q
C
q
V 

dq
C
q
Vdq
dW 


2
0
2
1
Q
C
dq
C
q
W
U
Q


 
 2
2
1
V
C
U 


24. Caso placas paralelas:
Ed
V 

  2
0
2
2
0
2
2
1
2
1
2
1
AdE
d
E
d
A
V
C
U 





2
0
2
1
E
Ad
U
uE 


Energía por unidad de
volumen, almacenada
por el campo eléctrico
2
2
12
10
854187817
.
8
Nm
C
o
-



  3
3
2
2
2
4
2
2
2
2
2
2
0
dim
m
J
Jm
J
C
J
Nm
C
m
V
Nm
C
E 






la densidad de energía en
cualquier campo eléctrico en un
punto dado es proporcional al
cuadrado de la magnitud del
campo eléctrico.

26. Capacitores con material dieléctrico
Un dieléctrico es un material no conductor,
como el hule, el vidrio o el papel encerado.
1
0






V
V

27. 1
0






V
V
0
0
0
0
0
0
C
V
Q
V
Q
V
Q
C 









la capacitancia cuando el capacitor está
lleno de material dieléctrico como sigue:

28. Un dieléctrico tiene las siguientes ventajas:
• Incrementa la capacitancia.
• Incrementa el voltaje máximo de operación.
• Proporciona un posible soporte mecánico entre las
placas, lo que permite que estén cerca una de la otra sin
tocarse, así reduce d y aumenta C.

29. Constante dieléctricas de algunos
materiales
Material Constante Material Constante
Vacío 1 Caucho 6,7
Aire 1,00059 Nylon 3,4
Baquelita 4,9 Papel 3,7
Cuarzo 3,78 Titanio 233
Vidrio
pyrex
5,6 Agua 80
Poliestireno 2,56 aceite 2,5
Teflón 2,1

30. +
-
Resistencia dieléctrica: es el voltaje máximo
antes de que se produzca una descarga.
Material Resistencia
Dieléctrica (V/m)
Aire seco 1.00059 3 x 106
Papel 3.7 16 x 106
Porcelana 6 12 x 106
Agua 80 -
Titanato de
Estroncio
233 8 x 106
Vacío 1.00000 -
