Descargar como PDF, PPTX
Subido porrgarciamatgeom
Congruencia de segmentos
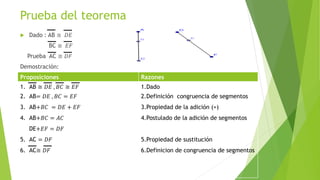
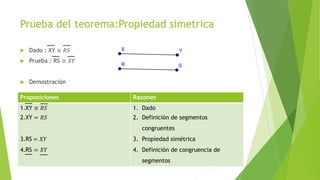
Este documento presenta el teorema de la congruencia de segmentos. Define un segmento como una parte de una recta entre dos puntos. Establece que la congruencia de segmentos es reflexiva, simétrica y transitiva. Demuestra la propiedad transitiva dando dos segmentos congruentes y mostrando que sus sumas también son congruentes. Justifica cada paso de la demostración usando propiedades como la adición y sustitución de segmentos. Finalmente, demuestra la propiedad simétrica mostrando que si dos segmentos son congruentes, también lo son en orden in
Congruencia de segmentos
- 1. Congruencia de segmentos Presentadopor Ricardo Garcia Ruiz Esc. Pretecnica Federico Asenjo
- 2. Definición Un segmentoes una parte de una recta que consiste de dos puntos, llamados extremos, y todos los puntos que están entre ellos. Como las medidas de los segmentos son números reales , entonces podemos usar propiedades del algebra para probar las relaciones entre las medidas de los segmentos. El teorema de la congruencia de los segmentos establece que la congruencia de los segmentos es reflexiva, simétrica y transitiva. Propiedad reflexiva AB ≅ AB Propiedad simétrica Si AB ≅ CD, entonces CD ≅ AB Propiedad transitiva Si AB ≅ 𝐶𝐷 𝑦 𝐶𝐷 ≅ 𝐸𝐹 , 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝐴𝐵 ≅ 𝐸𝐹
- 3. Prueba del teorema Dado : AB ≅ 𝐷𝐸 BC ≅ 𝐸𝐹 Prueba AC ≅ 𝐷𝐹 Demostración: Proposiciones Razones 1. AB ≅ 𝐷𝐸 , 𝐵𝐶 ≅ 𝐸𝐹 2. AB= 𝐷𝐸 , 𝐵𝐶 = 𝐸𝐹 3. AB+𝐵𝐶 = 𝐷𝐸 + 𝐸𝐹 4. AB+𝐵𝐶 = 𝐴𝐶 DE+𝐸𝐹 = 𝐷𝐹 5. AC = 𝐷𝐹 6. AC≅ 𝐷𝐹 1.Dado 2.Definición congruencia de segmentos 3.Propiedad de la adición (=) 4.Postulado de la adición de segmentos 5.Propiedad de sustitución 6.Definicion de congruencia de segmentos
- 4. Justifica cada pasode la demostracion Dado : ROPQ Prueba: RQ = RO + 𝑂𝑃 + 𝑃𝑄 Demostracion Razon 1 : Dado Razon 2: Postulado de la adicion de segmentos Razon 3: Postulado de la adicion de segmentos Razon 4: Propiedad de sustitucion (=) Proposiciones Razones 1.ROPQ 2.RQ= 𝑅𝑂 + 𝑂𝑄 3.OQ= 𝑂𝑃 + 𝑃𝑄 4.RQ= 𝑅𝑂 + 𝑂𝑃 + 𝑃𝑄 1.? 2.? 3.? 4.?
- 5. Prueba del teorema:Propiedadsimetrica Dado : XY ≅ 𝑅𝑆 Prueba : RS ≅ 𝑋𝑌 Demostración Proposiciones Razones 1.XY ≅ 𝑅𝑆 2.XY = 𝑅𝑆 3.RS = 𝑋𝑌 4.RS = 𝑋𝑌 1. Dado 2. Definición de segmentos congruentes 3. Propiedad simétrica 4. Definición de congruencia de segmentos