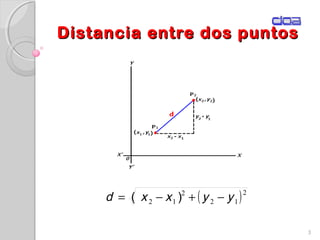
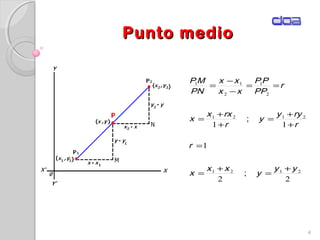
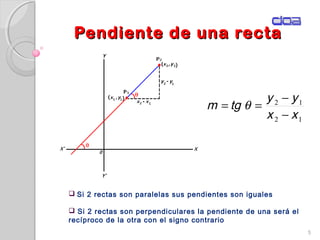
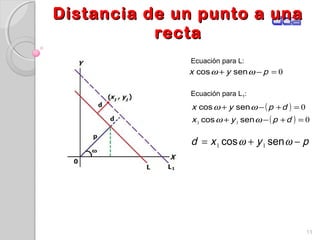
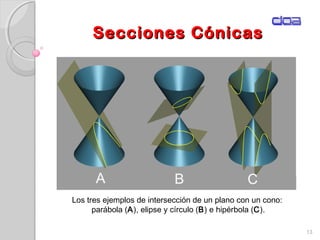
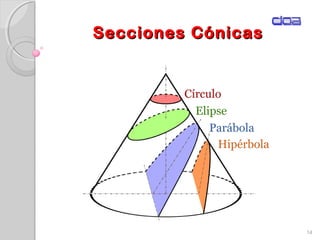
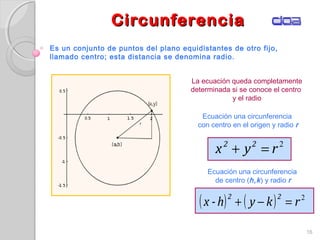
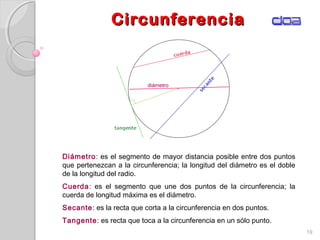
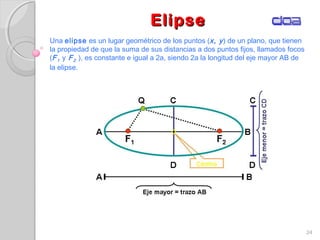
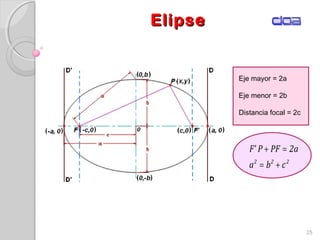
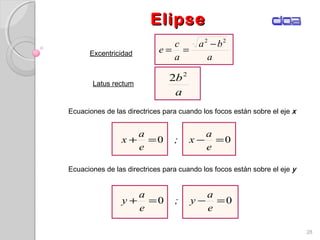
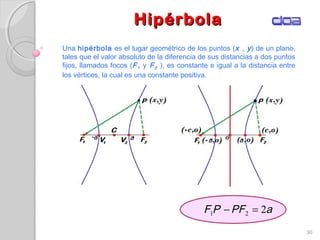
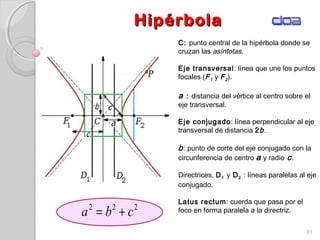
Este documento presenta los conceptos fundamentales de la geometría analítica, incluyendo coordenadas cartesianas, distancia entre puntos, ecuaciones de rectas y secciones cónicas. Explica las propiedades de parábolas, elipses, circunferencias e hipérbolas, y proporciona sus ecuaciones en diferentes formas. También define conceptos clave como foco, directriz, excentricidad, vértice y latus rectum para cada sección cónica.

1. MatemáticasMatemáticas
Geometría AnalíticaGeometría Analítica
1

2. Coordenadas RectangularesCoordenadas Rectangulares
2

3. Distancia entre dos puntosDistancia entre dos puntos
3
( )2
12
2
12 yyxxd −+−= )(

4. Punto medioPunto medio
4
22
1
11
2121
2121
2
1
2
11
yy
y
xx
x
r
r
ryy
y
r
rxx
x
r
PP
PP
xx
xx
PN
MP
+
=
+
=
=
+
+
=
+
+
=
==
−
−
=
;
;

5. Pendiente de una rectaPendiente de una recta
5
12
12
xx
yy
tgm
−
−
== θ
 Si 2 rectas son paralelas sus pendientes son iguales
 Si 2 rectas son perpendiculares la pendiente de una será el
recíproco de la otra con el signo contrario

6. Línea RectaLínea Recta
6
Representación gráfica del lugar geométrico cuya ecuación
sea de primer grado en dos variables.
Formas de la ecuación de una recta
a) PUNTO-
PENDIENTE
Recta que pasa por el punto P1(x1, y1) y cuya pendiente sea m
)( 11 xxmyy −=−
b) PENDIENTE-ORDENADA EN EL ORIGEN
Recta de pendiente m que corta al eje en y en el punto P1(0, b) y cuya
bmxy +=

7. Línea RectaLínea Recta
7
Formas de la ecuación de una recta
c) CARTESIANA
Recta que pasa por los puntos P1(x1, y1) y P2(x2, y2)
21
21
1
1
xx
yy
xx
yy
−
−
=
−
−
d) REDUCIDA O ABSCISA Y ORDENADA EN EL
ORIGEN
Recta que corta a los ejes x y y en los puntos (a, 0) y (0, b)
1=+
b
y
a
x

8. Línea RectaLínea Recta
8
Formas de la ecuación de una recta
e) GENERAL
Ecuación lineal o de primer grado
B
A
m −=
0=++ CByAx
B
C
b −=

9. Línea RectaLínea Recta
9
Formas de la ecuación de una recta
f) NORMAL
Recta que queda determinada si se conoce la longitud de la perpendicular a
ella trazada desde el origen (0, 0) y el ángulo que forma dicha perpendicular
con el eje x. La distancia p positiva a cualquier valor del ángulo ω .
ω
ω
ω
ω
ωω
sen
cos
gcot
tg
sen;cos
−=−=−=
==
1
11
m
pypx
( )
0
11
=−+
−−=−
−−=−
pyx
pxpy
xxyy
ωω
ω
ω
ω
ω
ω
sencos
)cos(
sen
cos
sen
gcot

10. Línea RectaLínea Recta
10
Reducción de la forma general a la normal
0=−+ pyx ωω sencos0=++ CByAx
0
1
1
222222
222222
22
2222
=
+±
+
+±
+
+±
+±
=−
+±
=
+±
=
+±
=
=+=+
=−==
=
−
==
BA
C
y
BA
B
x
BA
A
BA
C
p
BA
B
BA
A
BA
k
BAk
kCpkBkA
k
C
p
BA
;sen;cos
)(sencos
;sen;cos
sencos
2
ωω
ωω
ωω
ωω

11. Distancia de un punto a unaDistancia de un punto a una
rectarecta
11
0=−+ pyx ωω sencos
( ) 0=+−+ dpyx ωω sencos
( ) 011 =+−+ dpyx ωω sencos
pyxd −+= ωω sencos 11
Ecuación para L:
Ecuación para L1:

12. Secciones CónicasSecciones Cónicas
12
 El lugar geométrico de los puntos cuya relación de
distancias a un punto y una recta fijos es constante se define
como cónica o sección cónica.
 El punto fijo se llama foco.
 La recta fija se llama directriz.
 La relación constante se llama excentricidad.

13. Secciones CónicasSecciones Cónicas
13
Los tres ejemplos de intersección de un plano con un cono:
parábola (A), elipse y círculo (B) e hipérbola (C).

14. Secciones CónicasSecciones Cónicas
14

15. Secciones CónicasSecciones Cónicas
15
Excentricidad: en matemáticas, geometría, astronomía y otras ciencias
exactas, es un parámetro que determina el grado de desviación de una
sección cónica con respecto a una circunferencia.
Valores de la excentricidad en secciones cónicas:
Circunferencia e = 0
Elipse 0 < e < 1
Parábola e = 1
Hipérbola e > 1

16. CircunferenciaCircunferencia
16
Es un conjunto de puntos del plano equidistantes de otro fijo,
llamado centro; esta distancia se denomina radio.
Ecuación una circunferencia
con centro en el origen y radio r
2
ryx 22
=+
Ecuación una circunferencia
de centro (h,k) y radio r
( ) ( ) 2
rkyh-x
22
=−+
La ecuación queda completamente
determinada si se conoce el centro
y el radio

17. CircunferenciaCircunferencia
17
Ecuación general de una circunferencia
0FEyDxyx 22
=++++
4FED
2
1
r
2
D
4
4FED
2
E
y
2
D
x
F
4
E
4
D
4
E
Eyy
4
D
Dxx
0FEyyDxx
22
2222
222
2
2
2
22
−+=






−−
−+
=





++





+
−+=+++++
=++++
2
E
,
Reordenando
Completando cuadrados
Se tiene la ecuación
Con centro en el punto
y radio igual a

18. CircunferenciaCircunferencia
18
04FED
04FED
04FED
22
22
22
=−+
<−+
>−+La circunferencia es real si:
La circunferencia es imaginaria si:
La circunferencia representa un punto si:

19. CircunferenciaCircunferencia
19
diámetro
Diámetro: es el segmento de mayor distancia posible entre dos puntos
que pertenezcan a la circunferencia; la longitud del diámetro es el doble
de la longitud del radio.
Cuerda: es el segmento que une dos puntos de la circunferencia; la
cuerda de longitud máxima es el diámetro.
Secante: es la recta que corta a la circunferencia en dos puntos.
Tangente: es recta que toca a la circunferencia en un sólo punto.

20. ParábolaParábola
20
Una parábola es el lugar geométrico de los puntos que equidistan de
una recta (eje o directriz) y un punto fijo (foco).
PMPF =
( ) ( ) ax0yax
2
+=−+−
2

21. ParábolaParábola
21
PMPF =
( ) ( ) ax0yax
2
+=−+−
2
axx
axy
axy
aaxxyaaxx
4
4
4
22
2
2
2
22222
±=
−=
=
++=++−
Si el foco pertenece al eje y
Si el foco está a la izquierda
de la directriz
Elevando al cuadrado
Simplificando

22. ParábolaParábola
22
Si el vértice de la parábola tiene coordenadas (h,k), de eje paralelo
al eje de las x y foco a la derecha del vértice a una distancia a
( ) ( )
ahaxkkyy
ahxkyahx
442 22
22
−=+−
+−=−+−−
( ) ( ) ax0yax
2
+=−+−
2 ( ) ( )
( ) ( )
( ) ( )
( ) ( )kyahx
kyahx
hxaky
hxaky
−−=−
−=−
−−=−
−=−
4
4
4
4
2
2
2
2

23. ParábolaParábola
23
cbxaxy
cbyayx
++=
++=
2
2
Excentricidad
Latus rectum
1=e
a4

24. ElipseElipse
24
Una elipse es un lugar geométrico de los puntos (x, y) de un plano, que tienen
la propiedad de que la suma de sus distancias a dos puntos fijos, llamados focos
(F1 y F2 ), es constante e igual a 2a, siendo 2a la longitud del eje mayor AB de
la elipse.

25. ElipseElipse
25
222
cba
2aPFPF'
+=
=+
Eje mayor = 2a
Eje menor = 2b
Distancia focal = 2c

26. ElipseElipse
26
222
cba
2aPFPF'
+=
=+
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
( ) ( )
( )
222222
2
2
2
2
222
22
2
2
2
222
22222222
222
2222
2222
1
1
0
00
00
bayaxb
b
y
a
x
bca
ca
y
a
x
caa
caayaxca
ycxaacx
ycxycx
ycxycx
=+
=+
=−
=
−
+
−
−=+−
−+−=−
−+−=−++
=−+−+−++
-
-2a
2a
Haciendo que
Dividiendo por
Elevando al cuadrado y
reduciendo términos
Elevando al cuadrado y
simplificando

27. ElipseElipse
27
12
2
2
2
=+
a
y
b
x
12
2
2
2
=+
b
y
a
x
Ecuación de la elipse con centro en el origen y focos en el eje de las x
Ecuación de la elipse con centro en el origen y focos en el eje de las y

28. ElipseElipse
28
00 =−=+
e
a
y;
e
a
y
Excentricidad
Ecuaciones de las directrices para cuando los focos están sobre el eje x
Latus rectum
a
ba
a
c
e
22
−
==
a
b2
2
00 =−=+
e
a
x;
e
a
x
Ecuaciones de las directrices para cuando los focos están sobre el eje y

29. ElipseElipse
29
Si el centro de la elipse tiene coordenadas (h,k) y eje transversal
paralelo al eje x
( ) ( ) 12
2
2
2
=
−
+
−
b
ky
a
hx
( ) ( ) 12
2
2
2
=
−
+
−
a
ky
b
hx
Si el centro de la elipse tiene coordenadas (h,k) y eje transversal
paralelo al eje y
Ecuación general de una elipse siempre que A y B del mismo signo
022
=++++ FEyDxByAx

30. HipérbolaHipérbola
30
Una hipérbola es el lugar geométrico de los puntos (x , y) de un plano,
tales que el valor absoluto de la diferencia de sus distancias a dos puntos
fijos, llamados focos (F1 y F2 ), es constante e igual a la distancia entre
los vértices, la cual es una constante positiva.
aPFPF 221 =−

31. HipérbolaHipérbola
31
C: punto central de la hipérbola donde se
cruzan las asíntotas.
Eje transversal: línea que une los puntos
focales (F1 y F2).
a : distancia del vértice al centro sobre el
eje transversal.
Eje conjugado: línea perpendicular al eje
transversal de distancia 2b.
b: punto de corte del eje conjugado con la
circunferencia de centro a y radio c.
Directrices, D1 y D2 : líneas paralelas al eje
conjugado.
Latus rectum: cuerda que pasa por el
foco en forma paralela a la directriz.222
cba +=

32. HipérbolaHipérbola
32
aPFPF 221 =−Por definición
( ) ( ) aycxycx 200 2222
=−+−−−++ )()(

33. HipérbolaHipérbola
33
( ) ( )
( ) ( )
( )
1
020
200
2
2
2
2
22
22222
222
22222222
222
2222
2222
=−
=−
=−
−=−−
+−=−
−+−+=−++
=−+−−−++
b
y
a
x
ba
baayxb
bac
acayaxac
ycxaacx
ycxaycx
aycxycx
)(
)(
)()(
)()(
Dividiendo por
Haciendo que
Elevando al cuadrado y
reduciendo términos
Elevando al cuadrado y
simplificando
aPFPF 221 =−
222
cba +=

34. HipérbolaHipérbola
34
12
2
2
2
=−
b
x
a
y
12
2
2
2
=−
b
y
a
x
Ecuación de la hipérbola con centro en el origen y focos en el eje de las x
122
±=−ByAx
Ecuación general de una hipérbola con centro en el origen y
focos sobre los ejes de coordenadas
Ecuación de la hipérbola con centro en el origen y focos en el eje de las y

35. HipérbolaHipérbola
35
x
b
a
yx
a
b
y ±=±= ;
Excentricidad
Ecuaciones de las directrices para cuando los focos están sobre el eje x
y cuando están sobre el eje y
Latus rectum
Ecuaciones de las asíntotas para cuando el eje transversal es el eje x
y cuando el eje transversal es el eje y
a
c
e =
a
b 2
2
e
a
y
e
a
x ±=±= ;

36. HipérbolaHipérbola
36
Si el centro de la hipérbola tiene coordenadas (h,k) y eje transversal
paralelo al eje x
( ) ( ) 12
2
2
2
=
−
−
−
b
ky
a
hx
( ) ( ) 12
2
2
2
=
−
−
−
b
hx
a
ky
Si el centro de la hipérbola tiene coordenadas (h,k) y eje transversal
paralelo al eje y
Ecuación general de una hipérbola con centro en las coordenadas (h,k) y
ejes paralelos a los de las coordenadas x y y, siendo A y B del mismo signo
022
=+++− FEyDxByAx

37. HipérbolaHipérbola
37
( ) ( )hx
b
a
kyhx
a
b
ky −±=−−±=− ;
Ecuaciones de las asíntotas de una hipérbola con centro
en las coordenadas (h,k) para cuando el eje transversal es el eje x
y cuando el eje transversal es el eje y
Ecuaciones de las asíntotas para cuando el eje transversal es el eje x
y cuando el eje transversal es el eje y
x
b
a
yx
a
b
y ±=±= ;