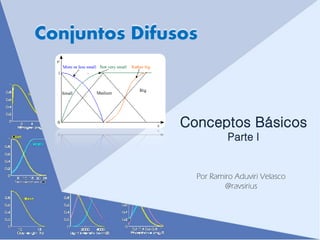
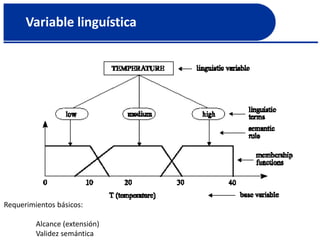
Este documento introduce los conceptos básicos de conjuntos difusos y lógica difusa. Explica que los conjuntos difusos permiten representar información vaga mediante funciones de membresía graduadas en lugar de funciones características binarias. También describe cómo se definen y representan conjuntos difusos, incluidas sus operaciones y propiedades como el soporte, núcleo y cortes alfa. Finalmente, introduce formas comunes de funciones de membresía y el concepto de complemento de conjuntos difusos.

1. Conjuntos DifusosConjuntos Difusos
Conceptos Básicos
Parte I
Por Ramiro Aduviri Velasco
@ravsirius

2. ¿Qué es esta “cosa difusa”?
Diccionario de Webster: difuso
1. Cubierto con algo o similar a algo borroso
2. No claro: confuso
3. Borroso, vago.

3. Conjuntos difusos y lógica difusa
Métodos para la representación de incertidumbres y
razonamientos bajo incertidumbre.
Tipos de incertidumbre:
casualidad, fortuito (estocástico)
imprecisión, vaguedad, ambigüedad (no estocástico)

4. Conjuntos difusos y lógica difusa
Propuesto en 1965 por L.A. Zadeh
70s primera aplicación, control fuzzy (Mamdani)
80s aplicaciones industriales, operación del tren,
reconocimiento por patrón
90s productos de consumo, carros, hardware y
software especiales.
El término “lógica difusa” con frecuencia también denota a
la teoría de conjuntos difusos y sus aplicaciones (p.e., control
de lógica difusa).

5. Precisión contra pertinencia

6. Teoría clásica de conjuntos
Un conjunto es una colección de objetos con una propiedad común.
Ejemplos:
Conjunto de números naturales menores a 5:
A = {1,2,3,4}
Disco unitario en el plano complejo:
A = {zIz Є C, IzI  1}
Una línea en IR2:
A = {(x, y)I ax + by + c = 0 [x,y,a,b,c Є IR]}

7. Representación de conjuntos
Enumeración de elementos:
A = {x1, x2, …, xn}
Definición por propiedad:
A = {x Є X I x tiene propiedad P}
Función característica:
A(x): X  {0, 1}
1, si x miembro de A
A(x) =
0, si x no es miembro de A

8. Operaciones con conjuntos
Intersección: C = A  B
Unión: C = A  B
Complemento: C = A
C contiene elementos que pertenecen a A y B
Función característica:
C = min{A, B}
C contiene elementos que pertenecen a A o a B
Función característica:
C = max{A, B}
C contiene elementos que no pertenecen a A
Función característica:
C =1  A

9. ¿Por qué conjuntos difusos?
 Conjuntos clásicos son para conceptos bien definidos, pero…
 Poco útil para representar información en términos de conceptos
vagos como:
• una persona alta, carretera resbaladiza, buena agua, …
• quiero comprar un carro grande con consumo moderado
• si la temperatura de demasiado baja, incremente más
calor.

10. Enfoque de conjuntos clásicos
Un conjunto es una colección de elementos con cierta
propiedad.
“Jhon es alto” . . . verdadero o falso
Altura de Jhon:
hJhon = 180.0 A(180.0) = 1(verdadero)
hJhon = 179.5 A(179.5) = 1(falso)
Ejemplo:

11. Enfoque de conjuntos difusos
Conjunto con membresía graduada, es decir, un elemento
pertenece a un conjunto para un grado dado.
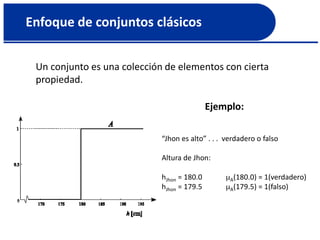
“Jhon es alto” … grado de verdad
Altura de Jhon
hJhon = 180.0 A[180.0] = 0.55
hJhon = 179.5 A[179.5] = 0.5
hJhon = 201.0 A[201.0] = 1
Ejemplo:

12. Subjetivo y dependiente del contexto

13. Variable linguística
Requerimientos básicos:
Alcance (extensión)
Validez semántica

14. Soporte de un conjunto difuso
sup(A) = {x I A(x) > 0}
Soporte es un conjunto ordinario.

15. Corazón (núcleo) de un conjunto difuso
cor(A) = {x I A(x) = 1}
Corazón es un conjunto ordinario.

16. cut de un conjunto difuso
A = {x I A(x) > } o A = {x I A(x)  }
A es un conjunto ordinario.

17. Conjuntos difusos convexos y no convexos
Un conjunto difuso es convexo  todos sus -cuts son conjuntos convexos.

18. Conjuntos difusos no convexos: un ejemplo
Epoca de alto riesgo para póliza de seguros en autos.

19. Representación de conjuntos difusos
 Apropiado como una lista de pares membresía/elemento:
 Como una lista de pares -nivel/-cut:
 Fórmula analítica para la función de membresía
o de forma más general
donde d(x, v) es una medición de desigualdad.
Varias notaciones de taquigrafía: A(x), A(x), a

20. Formas de funciones de membresía

21. Cantidades difusas y Singletons
Regresión lineal difusa: y = 3~x1 + 5~x2

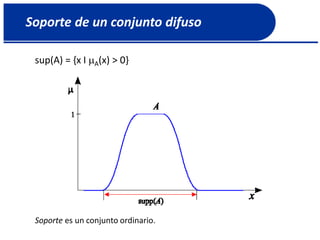
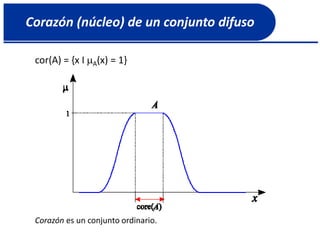
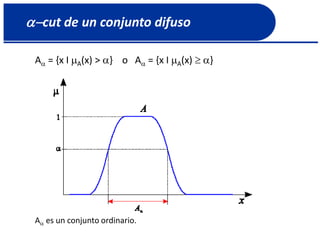
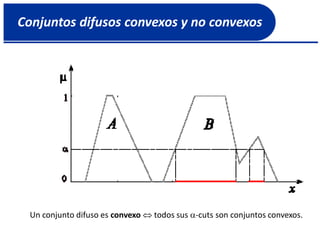
22. Complemento de un conjunto difuso
c: [0, 1]  [0, 1]
A(x)  c(A(x))
Axiomas fundamentales
Condiciones de límite  c se comporta como el complemento ordinario
c(0) = 1 c(1) = 0
Ningún incremento monotónico
a, b  [0, 1], si a < b, entonces c(a)  c(b)
Otros axiomas
 c es una función continua.
 c es involutive, lo que significa que
c(c(a)) = a, a  [0, 1]