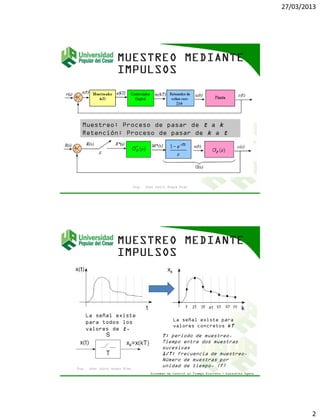
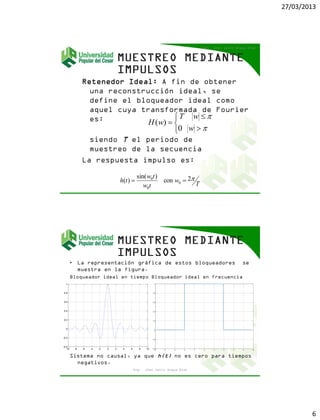
El documento describe los procesos de muestreo y retención de datos. Explica que el muestreo convierte una señal continua en una secuencia discreta de valores mediante la multiplicación por impulsos de Dirac, mientras que la retención reconstruye una señal continua a partir de valores discretos. También compara los retenedores de orden cero y uno, y explica que el orden cero mantiene cada muestra constante hasta la siguiente, mientras que el orden uno interpola linealmente.