Derivadas teoria-ejercicios-resueltos

INSTITUTO UNIVERSITARIO DE TECNOLOGÍA
“JOSÉ ANTONIO ANZOÁTEGUI”
EL TIGRE-EDO-ANZOÁTEGUI
Cátedra: Matemática II
Especialidades: Mecánica - Química
Lic. MSc. DÁMASO ROJAS

DEFINICIÓN DE LA DERIVADA.
INTERPRETACIÓN GEOMÉTRICA

Sea P un punto fijo de la curva y sea Q un punto móvil de esa curva,
próximo a P. Considérese la recta que pasa por P y Q, llamada secante. La recta
tangente en P es la posición límite (si existe) de la secante, cuando Q se mueve
hacia P a lo largo de la curva.
Sea ƒ una función definida en un intervalo abierto que contiene al número
a. En la figura 1.1 se ilustran la gráfica de ƒ y una recta secante lpq que pasa
por P ( a , ƒ ( a ) ) y Q( x, ƒ( x )). La recta de trazo punteado l representa
una posible recta tangente en el punto P.
lPQ
l Q
Y

P

a x X

La pendiente m de l se define como el valor de límite de la pendiente de lPQ
f ( x) − f (a)
cuando Q tiende a P. Así por la definición tenemos: m = lím
x→0 x−a
siempre y cuando el límite exista. Si se introduce una nueva variable h tal
que x = a + h (es decir, h = x - a), como se ilustra en la figura 1.2.
l lPQ
Y Q

P

a a+h X ( fig. 1.2 )

se obtiene la siguiente fórmula para la pendiente m = Lím f a h f a , que es
( + )− ( )
h →0 h
equivalente a la anterior. El límite anterior es uno de los conceptos
fundamentales del cálculo y se llama derivada de la función ƒ en a.
1
E-mail: damasorojas8@gmail.com, damasorojas8@galeon.com, joeldama@yahoo.com


Definición 1. Sea ƒ una función definida en un intervalo abierto que
contiene a a. La derivada de ƒ en a, denotada por ƒ’(a), está dada por
f ( a + h) − f ( a) , si este límite existe.
f ′( a) = Lím
h→0 h

Si este límite existe, decimos que ƒ es diferenciable en a. Encontrar la
derivada se llama derivación; la parte de cálculo asociada con la derivada se
llama cálculo diferencial.
La diferenciabilidad implica continuidad. Si una curva tiene tangente en un
punto, la curva no puede dar un salto en ese punto. La formulación precisa de
este hecho es un teorema importante.
Teorema 1. Si existe ƒ’(a), entonces ƒ es continua en a.
Una función ƒ es derivable en un intervalo abierto (a,b) si lo es en todos los
números c de (a,b). También se considerarán funciones que son derivables en
un intervalo infinito (- ∞ , a), (a,∞) o bien (- ∞ , ∞).
Para intervalos cerrados usaremos la siguiente definición.
Definición 2. Una función ƒ es derivable en un intervalo cerrado [a , b], si
f (a + h ) − f (a ) f (a + h) − f (a )
lo es en el intervalo (a , b) y los límites lí m lím
h→ 0
+ h −
h→0 h
existen.
Los límites por la derecha y por la izquierda en la definición anterior, se
llaman derivada por la derecha y derivada por la izquierda de ƒ en a y b,
respectivamente.
La derivada de una función en intervalos de la forma [a, b), [a,∞), (a ,b] o
bien (- ∞ , b] se define usando los límites por la derecha o por la izquierda en
uno de los puntos extremos. Si ƒ está definida en un intervalo abierto que
contiene a a, entonces ƒ ’(a) existe si y sólo si las derivadas por la derecha y
por la izquierda en a existen y son iguales.
El inverso del teorema 1. Es falso. Si una función ƒ es continua en c, no se
sigue que ƒ tenga derivada en c. Esto se ve con facilidad examinando la función
ƒ (x)=| x | en el origen. Esta función, por cierto, es continua en cero, pero no
tiene derivada ahí. (Demostración a cargo del lector)
El argumento recién presentado demuestra que en cualquier punto en el
que la gráfica de ƒ tiene un pico o presenta una esquina aguda, es continua,
pero no diferenciable.
Suponiendo que la función ƒ es derivable en a, se puede enunciar la
siguiente definición.
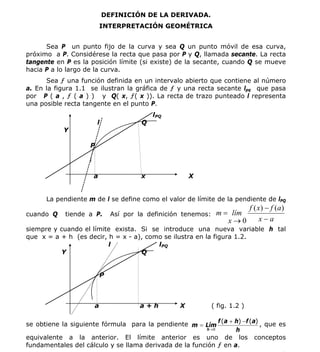
Definición 3. Recta tangente: La pendiente de la recta tangente a la
gráfica de ƒ en el punto (a, ƒ(a)) es ƒ’(a ).

2


Derivada como una función
Si ƒ es derivable para todo x en un intervalo entonces, asociando a cada x
el número ƒ’(x), se obtiene una función ƒ’ llamada derivada de f. El valor de
ƒ’, en x está dado por el siguiente límite. f ′ = lím f(x + h) − f(x), (Límite
(x) h
h→0
unilateral), nótese que el número x es fijo, pero arbitrario y el límite se toma
haciendo tender h a cero. Derivar ƒ(x) o encontrar la derivada de ƒ(x) significa
determinar ƒ’(x).
En los siguientes ejercicios se determinará la primera derivada por
definición, o la pendiente de la recta tangente a la curva en un punto dado.

Ejercicios Resueltos:

1) y = 5 x → f(x) = 5 x
f(x + Δx) − f(x)
f ′(x) = Lím → Aplicando la ecuación
Δx → 0 Δx

f ′(x) = Lím
5 ( )
x + Δx −5 x
Δx → 0 Δx
5 ⎡ x + Δx − x ⎤ ⎦ = f ′(x) = 0 IND
f ′(x) = Lím ⎣
Δx → 0 Δx 0
5 ⎡ x + Δx − x ⎤ ⎡ x + Δx + x ⎤
f ′(x) = Lím ⎣ ⎦ .⎣ ⎦
Δx → 0 Δx ⎡ x + Δx + x ⎤
⎣ ⎦
5 (x + Δx − x) 5 Δx
f ′(x) = Lím =
Δx → 0
Δx ⎡ x + Δx + x ⎤
⎣ ⎦ Δx ⎡ x + Δx +
⎣ x⎤
⎦
1 5
f ′(x) = 5 Lím = f ′(x) =
Δx → 0 x + Δx + x 2 x

3


1 1
−
1 x + Δx − 3 x −3 0
2) f(x) = ⇒ f ′(x) = Lím = ind
x −3 Δx → 0 Δx 0
x −3 − x + Δx − 3
x + Δx − 3 x − 3 x −3 − x + Δx − 3
f ′(x) = Lím
Δx → 0 Δx
= Lím
Δx → 0
Δx [ x + Δx − 3 x −3 ]
1
Aplicando conjugada :
( x −3 − x + Δx − 3 ) ⎡ x − 3 + x + Δx − 3 ⎤
f ′(x) = Lím
Δx → 0
Δx [ ⎢
]
x + Δx − 3 x − 3 ⎢ x − 3 +
⎣
⎥
x + Δx − 3 ⎥
⎦
x − 3 − x − Δx + 3
f ′(x) = Lím
Δx → 0
[
Δx (x − 3 ) x + Δx − 3 + (x + Δx − 3 ) x − 3 ]
1
f ′(x) =
(x − 3 ) (x − 3 ) + (x − 3 ) (x − 3 )
1 1
f ′(x) = ⇒ f ′(x) =
( x − 3 )3 + ( x − 3 )3 2 (x − 3)
3

3 x +Δx−2 − 3 x−2 0
3) f(x) = 3 x−2 f′(x) = Lím = ind
Δx→0 Δx 0
a3 − b3 = (a −b) (a2+ab+b2) Identidad
Donde: a = 3( x+Δx−2) ; b = 3 x−2

⎡3( x +Δx−2) − 3 x−2⎤ ⎡3( x + Δx − 2)2 + 3( x + Δx − 2) 3 x − 2 + 3( x − 2)2⎤
⎢
⎣ ⎥⎢
⎦⎣ ⎥
⎦
f′(x) = Lím
Δx→0 ⎡ ⎤
Δx⎢3( x + Δx − 2)2 + 3( x + Δx − 2) 3 x − 2 + 3( x − 2)2⎥
⎢
⎣ ⎥
⎦
3(( x + Δx − 2))3 − 3( x − 2)3
f′(x) = Lím
Δx→ ⎡ ⎤
Δx⎢3( x + Δx − 2)2 + 3( x + Δx − 2) 3 x − 2 + 3( x − 2)2⎥
0

⎣ ⎦

4


x + Δx − 2 − x + 2
f ′(x) = Lím
Δx → 0 ⎡ 3 x − 2 + 3 ( x − 2 )2 ⎤
Δx ⎢3 ( x + Δx − 2 )2 + 3 ( x + Δx − 2 )
⎥
⎣ ⎦
1
f ′(x) = Lím
⎡3
Δx → 0
2 3 ( x + Δx − 2 ) 3 x − 2 + 3 ( x − 2 )2 ⎤
⎢ ( x + Δx − 2 ) + ⎥
⎣ ⎦
1 1
f ′(x) = ⇒ f ′(x) =
3 ( x − 2 ) 2 + 3 ( x − 2 ) 2 + 3 ( x − 2 )2 33 ( x − 2 )2

1 1
−
x x 1 x + Δx x 0
4) f(x) = → f(x) = → f(x) = ⇒ f ′(x) = Lím = ind
Δx 0
x3 x x x Δx → 0

x− x + Δx
x x + Δx ( x− x + Δx ) ⎡ x + x + Δx ⎤
f ′(x) = Lím
Δx → 0 Δx
⇒ f ′(x) = Lím
Δx → 0
Δx [ x + Δx x ⎢
⎢
⎣ ] x +
⎥
x + Δx ⎥
⎦
x − x − Δx 1
f ′(x) = Lím
Δx → 0
Δx x [ x + Δx + (x + Δx ) x ] ⇒ f ′(x) = Lím
Δx → 0
x x + Δx + (x + Δx) x
1 1 1
f ′(x) = ⇒ f ′(x) = ⇒ f ′(x) =
x x +x x x3 + x3 2 x3

5) F(x) = x + 5
x + Δx + 5 − x + 5 0
y´= Lím = Ind
Δx → 0 Δx 0
⎡ x + Δx + 5 − x + 5 ⎤ ⎡ x + Δx + 5 + x + 5 ⎤
y´ = Lím ⎢ ⎥⎢ ⎥
Δx → 0
⎢
⎣ Δx ⎥ ⎢ x + Δx + 5 + x + 5 ⎥
⎦⎣ ⎦
(x + Δx + 5 ) − (x + 5 ) ⇒ y´= Lím x + Δx + 5 − x + 5
y´ = Lím
Δx → 0
[
Δx x + Δx + 5 + x + 5 Δx → 0
]
Δx x + Δx + 5 + x + 5 [ ]
1 1
y´= Lím ⇒ y´ =
Δx → 0
x + Δx + 5 + x + 5 2 x+5

5


1 1
−
1 3 (x + Δ x ) 3x 0
6)f (x) = ⇒ f´(x) = Lím = IND
3x Δx → 0 Δx 0
3x − 3 (x + Δ x )
3 (x + Δ x ) 3x 3x − 3 (x + Δ x )
f´(x) = Lím
Δx → 0 Δx
⇒ f´(x) = Lím
Δx → 0
Δx [ 3 (x + Δ x ) 3x ]
1
[ 3x − 3 (x + Δ x ) ⎡ 3x ] + 3 (x + Δ x ) ⎤
f´(x) = Lím
Δx → 0
Δx [ 3 (x + Δ x )
⎢
3x ⎢ 3x
⎣ ] +
⎥
3 (x + Δ x ) ⎥
⎦
3x − 3x − 3 Δ x
f´(x) = Lím
Δx → 0
Δx [ 3 (x + Δ x ) (3x ) 3x 3 (x + Δ x ) ]
− 3
f´(x) = Lím
Δx → 0
[ 3 (x + Δ x ) (3x ) 3x 3 (x + Δ x ) ]
− 3 − 3 − 3
f´(x) = Lím
Δx → 0
3x (3x ) + 3x (3x )
⇒ f´(x) =
2 [ 3x (3x ) ] ⇒ f´(x) =
2 27 x 3

2x − 3
7) f(x) =
3x + 4

f´(x) = Lím
( 2x + 2Δx − 3)
−
( 2x − 3)
=
0
Ind
Δx → 0 ( 3x + 3Δx + 4 ) ( 3x + 4) 0

f´(x) = Lím
( 3x + 4 ) [ 2x + 2 Δ x − 3 ] − ( 3x + 3 Δ x + 4 ) ( 2x − 3)
Δx → 0 ( 3x + 3 Δ x + 4 ) ( 3x + 4 )

6x 2 + 6xΔx − 9x + 8x + 8 Δ x − 12 − 6x 2 + 9x − 6xΔx + 9 Δ x − 8x + 12
f´(x) = Lím
Δx → 0 ( 3x + 3 Δ x + 4 ) ( 3x + 4 )
Ordenando:
6x 2 + 6xΔx − 9x + 8x + 8 Δ x − 12 − 6x 2 + 9x − 6xΔx + 9 Δ x − 8x + 12
f´(x) = Lím
Δx → 0 Δx ⎡ ( 3x + 3 Δ x + 4 ) ( 3x + 4 ) ⎤
⎣ ⎦

17 Δx 17
f´(x) = Lím ⇒ f´(x) =
Δx → 0 Δx ⎡ ( 3x + 3 Δ x + 4 ) ( 3x + 4 ) ⎤
⎣ ⎦ ( 3x + 4 )
2

6


1 ⎛ 1 1 ⎞ 0
8) F(x) = + x ⇒ F´(x) = Lím ⎜ + x + Δx − − x⎟ =
⎟ 0
x Δx → 0 ⎜ x + Δx x
⎝ ⎠
x + (x + Δx ) x − (x + Δx ) − x 2 (x + Δx )
2

F´(x) = Lím
Δx → 0 (x + Δx )
F´(x) = Lím
( )
x + x 2 + 2x Δx + Δx 2 x − x − Δx − x 3 − x 2 Δx
Δx → 0 (x + Δx ) x
x + x 3 2x 2 Δx + x Δ x 2 − x − Δx − x 3 − x 2 Δx
F´(x) = Lím
Δx → 0 (x + Δx ) x
Δx ⎡ x 2 + xΔ − 1⎤
x 2 Δx + x Δ x 2 − Δx ⎢
⎣ ⎥
⎦
F´(x) = Lím ⇒ F´(x) = Lím
Δx → 0 Δx [x (x + Δx )] Δx → 0 Δx [x (x + Δx )]
x2 − 1 1
F´(x) = ⇒ F´(x) = 1 − 2
x2 x

f(x + Δx) − f(x)
9) f(x) = Sen x f ′(x) = Lím
Δx → 0 Δx
Sen (x + Δx) − Sen x 0
f ′(x) = Lím = ind
Δx → 0 Δx 0
f ′(x) = Lím
(Sen x Cos Δx + Cos x Sen x )− Sen x
Δx → 0 Δx
Cos x Sen Δx + Sen x Cos Δx − Sen x
f ′(x) = Lím
Δx → 0 Δx
f ′(x) = Lím
(Cos x Sen Δx )+ Sen x [Cos Δx − 1 ]
Δx → 0 Δx
Cos x Sen Δx Sen x [Cos Δx −1 ]
f ′(x) = Lím + Lím
Δx → 0 Δx Δx → 0 Δx
f ′(x) = Cos x Lím
Sen Δx
+ Sen x Lím
[Cos Δx −1]

Pero conocemos : Lím
Sen Δx
=1 ; Lím
[1 − Cos Δx ]= 0
Δx
Δx → 0 Δx → 0 Δx
f ′(x) = Cos x Lím
Sen Δx
− Sen x Lím
[1 − Cos Δx ]
f ′( x ) = Cos x

7


10) f(x) = Cosx
f(x + Δx) − f(x)
f ′(x) = Lím
Δx→0 Δx
Cos(x +Δx) − Cosx 0
f ′(x) = Lím = ind
Δx→0 Δx 0
CosxCos(Δx) − SenxSen(Δx) − Cosx CosxCos(Δx) − Cosx −SenxSen(Δx)
f ′(x) = Lím ⇒f′(x) = Lím
Δx→0 Δx Δx→0 Δx
Cosx [Cos(Δx) − 1] − Senx Sen(Δx) Cosx [ Cos(Δx) − 1] Senx Sen(Δx)
f ′(x) = Lím ⇒f′(x) = Lím − Lím
Δx→0 Δx Δx→0 Δx Δx→0 Δx

f ′(x) =CosxLím
[Cos(Δx)− 1] − SenxLím Sen(Δx)

f ′(x) =−CosxLím
[1 − Cosx] − SenxLím Sen(Δx)

Conociendo: Lím
[1 − Cosx] = 0 ; Lím Sen(Δx) = 1⇒f′(x) = − Senx
Nota : Lím Sen x = 0 Lím Cos x = 1
Δx → 0 Δx → 0

11) f(x) = tg x
tg(x + Δ x) − tg (x) 0
f ′ (x) = Lím = ind
Δx → 0 Δx 0

tg a + tg b
U tilizando la identidad: tg(a + b) =
1 − tg a tg b

tg x + tg Δ x
− tg(x)
1 − tg x tg Δ x
f ′ (x) = Lím
Δx → 0 Δx

8


(tgx + tg(Δx)) − tgx[1 − tgx tg(Δx)]

f ′(x) = Lím
(1 − tgx tg(Δx))
Δx→0 Δx
tg(Δx) ⎡1 − tg x⎤
2
2 ⎢ ⎥
/ + tg(Δx) − / + tg x tg(Δx)
tgx tgx ⎣ ⎦
f ′(x) = Lím ⇒ f ′(x) = Lím
Δx→0 Δx[1 − tgx tg(Δx)] Δx→0 Δx[1 − tgx tg(Δx)]

tg(Δx) tg(Δx) 1
f ′(x) = ⎡1 − tg x⎤ Lím ⇒ f ′(x) = ⎡1 − tg x⎤ Lím
2 2
⎢ Lím
⎥ Δx→0 Δx Δx→0 1 − tgx tg(Δx)
⎢
⎣ ⎥ Δx→0 Δx[1 − tgx tg(Δx)]
⎦ ⎣ ⎦

Sen(Δx)
Cos(Δx) Sen(Δx)
f ′(x) = ⎡1 − tg x⎤ Lím ⇒ f ′(x) = ⎡1 − tg x⎤ Lím
2 2
⎢
⎣ ⎥
⎦ Δx→0 Δx ⎢
⎣ ⎥ Δx→0 ΔxCos(Δx)
⎦
Sen(Δx) 1
f ′(x) = ⎡1 − tg x⎤ Lím
2
⎢ Lím
⎥ Δx→0 Δx Δx→0 CosΔx ⇒ f ′(x) = 1 − tg 2 x
⎣ ⎦
Sec 2 x = 1 − tg 2 x ⇒ f ′(x) = Sec 2 x

f(x + Δx) − f(x)
12) f(x) = e x f ′(x) = Lím
Δx → 0 Δx

e − ex
x + Δx
0 e e −e
x Δx x
f ′(x) = Lím = ind ⇒ f ′(x) = Lím
Δx → 0 Δx 0 Δx → 0 Δx

e
Δx
−1 a
Δx
−1
f ′(x) = e x Lím Pero : Lím = 1 ⇒ f ′(x) = e x

9


Log a (x + Δx) − Log a x 0
13) f ( x) = Loga x ⇒ f ′(x) = Lím = ind
Δx →0 Δx 0
1 ⎡ ⎡ (x + Δx) ⎤ ⎤
f ′(x) = Lím ⎢Log a ⎢ ⎥⎥
Δx →0 Δx ⎣ ⎣ x ⎦⎦
1 ⎡ Δx ⎤
f ′(x) = Lím Loga ⎢1 + x>0
Δx →0 Δx
⎣ x ⎥⎦
1
f ′(x) = Loga Lím ⎡1 + ⎤
Δx Δx Δx
Cambio t = → Δx = tx Δx = 0 → t=0
Δx →0 ⎣ x ⎦ x

((1 + t ) )
1
f ′(x) = Loga Lím [1 + t ]
1 1 x
tx
→ f ′(x) = Loga Lím t
t →0 t →0

1 1 1
f ′(x) = Loga Lím (1 + t ) t ⇒ f ′(x) = Loga Lím (1 + t ) t
1
t →0 x x t →0

1 1
Pero Lím (1 + t ) t = e ⇒ f ′(x) = Loga e
t →0 x

14) y = Ln ax f(x) = Ln ax
⎡ a(x + Δx) ⎤
Ln ⎢ ⎥
Ln a(x + Δx) − Ln ax ⎣ ax ⎦
f ′(x) = Lím ⇒ f ′(x) = Lím
⎡ (x + Δx) ⎤ ⎡ Δx ⎤
Ln ⎢ ⎥ Ln ⎢1 +
⎣ x ⎦ ⇒ f ′( x) = Lím ⎣ x ⎥⎦
f ′(x) = Lím

( )
⎡ 1
⎤
1 ⎡ Δx ⎤ ⎢ Ln 1 + Δx
Δx
⎥
f ′( x ) = Lím Ln (1 + ) ⎥ ⇒ f ′( x ) = Lím
Δx → 0 Δx ⎢ Δx → 0 ⎢ ⎥
⎣ x ⎦ x
⎣ ⎦
Δx
Cambio t = ⇒ Δx = tx ⇒ Δx → 0 t → 0
x
1 1 1
1 1
( ) (
f ′(x) = Lím Ln 1 + t tx ⇒ f ′(x) = Lím Ln 1 + t t ⇒ f ′(x) = Ln Lím
t →0 t →0 x
) x t →0
(1 + t ) t

1
1 1
t →0
( )
Pero Lím 1 + t t = e ⇒ f ′( x) = Ln e
x
→ f ′( x) =
x

10


Ejercicios de aplicación de la definición de la Derivada.

1.- Determinar una ecuación de la recta tangente a la curva y = 2 x 2 + 3 en
el punto (-1,5).

mtg = Lím
f ( x + Δx ) − f(x)
,en ese punto m(x ) = Lím 1
(
f x + Δx − f(x )
1 )
Δx→0 Δx 1 Δx→0 Δx

m(x ) = Lím
(
2 x + Δx
1 )
2
(
+ 3 − 2x 2 + 3
1 )
⇒ m(x ) = Lím 1
2x 2 + 4x Δx + 2Δx2 + 3 − 2x 2 − 3
1
/
1
/
1 Δx→0 Δx 1 Δx→0 Δx

4x Δx + 2Δx2 Δx ⎡ 4x + 2Δx⎤
m(x ) = Lím 1 ⇒ m(x ) = Lím ⎣ 1 ⎦ ⇒ m(x ) = 4x
1 Δx→0 Δx 1 Δx→0 Δx 1 1

sust. el valor de x en la m(x ) ⇒ m(x ) = 4x ⇒ m( − 1) = 4( − 1) ⇒ m = − 4
1 1 1 1
utilizando la ecuación punto − pendiente de la recta
y − y = m(x − x ) → y − 5 = − 4(x + 1) ⇒ Recta tg :4x + y − 1 = 0
1 1

2x
2.- Dada la función y = calcular la ecuación de al recta tangente
x −1
y la ecuación de la recta normal a la curva en el punto (-1,1).

2( x + Δx ) 2x
−
x + Δx −1 x− 1 0
m( x )=Lím = ind
1 Δx → 0 Δx 0
2( x + Δ x ) 2x 2( x + Δ x ) 2x 2( x + Δ x ) 2 x
− + −
x + Δx −1 x− 1 x + Δx −1 x− 1 x + Δ x −1 x − 1
m( x )=Lím ⇒ m( x )=Lím
1 Δx → 0 Δx 2( x + Δ x ) 2x 1 Δx → 0 ⎡ 2( x + Δ x ) 2x ⎤
+ Δx ⎢ + ⎥
x + Δx −1 x− 1 ⎣ x + Δ x −1 x− 1 ⎦

11


2(x + Δx)(x −1) − 2x(x + Δx −1) 2x2 − 2x + 2xΔx − 2ΔΔ− 2x2 −2xΔx + 2x

m(x1) = Lím
(x + Δx −1)(x −1) ⇒ m(x1 ) = Lím
(x + Δx −1)(x −1)
Δx →0 ⎡ 2(x + Δx) 2x ⎤ Δx →0 ⎡ 2(x + Δx) 2x ⎤
Δx⎢ + ⎥ Δx⎢ + ⎥
⎢ x + Δx −1
⎣ x− 1⎦
⎥ ⎢ x + Δx −1
⎣ x− 1⎥
⎦
− 2ΔΔ
(x + Δx −1)(x −1) //
− 2Δx
m(x ) = Lím ⇒ m(x ) = Lím
1 Δx →0 ⎡ 2(x + Δx) 2x ⎤ 1 Δx →0 ⎡ 2(x + Δx) 2x ⎤
Δx⎢ + ⎥ /
Δx(x + Δx −1)(x −1)⎢ + ⎥
⎢ x + Δx −1
⎣ x− 1⎥
⎦ ⎢ x + Δx −1
⎣ x− 1⎥
⎦
−2
m(x ) = Lím
1 Δx →0 ⎡ 2(x + Δx) 2x ⎤
(x + Δx −1)(x −1)⎢ + ⎥
⎢ x + Δx −1
⎣ x− 1⎥
⎦
−2 −2
1 Δx →0 2 ⎡ 2x 2x ⎤ 1 Δx →0 2x 2
( x−1) ⎢ x − 1 + x − 1 ⎥ 2
x− 1
( x−1)
⎢
⎣ ⎥
⎦
−1 −1 −1 −1 −1
m(x ) = ⇒ m(x ) = ⇒m(−1) = m(−1) = → m(−1) =
1 4 1 3 − 2(−8) 16 4
2x( x−1) (2x) ( x −1)
x− 1
Para la recta tangente : y −y1 = m(x − x1 ) Punto (−1,1)
1 −1
y −1 = − (x +1) ⇒ 4y − y = − x −1 ⇒ x + 4y − 3 = 0 Nota : mn =
4 mtg
−1 −1
Para R.N : y − y1 = (x − x1 ) ⇒ y −1 = (x +1) ⇒ y −1 = 4(x +1) ⇒4x − y + 5 = 0 (R.N.)
mt ⎛ − 1⎞
⎜ ⎟
⎝ 4 ⎠

3.- Calcule la “pendiente media” de al curva
y = 2x en el intervalo (1, 5)

y =2x Punto [1, 5 ]
f(x + Δx) − f(x) f(x + Δx) − f(x)
m = → m =
n Δx n x −x
2 1

x +Δx 1+ 4
2 −2 x 2 + 21 25 +2 15
m = ⇒ m = ⇒ m = ⇒ m =
n x −x n 4 n 4 n 2
2 1

12


1
4.- Determine la ecuación de la recta tangente a la curva y = en el punto
5x − 2
1
(1 , )
3
1 1
−
f ( x + Δx ) − f ( x ) 5( x + Δx ) − 2 5 x − 2 0
m = Lím ⇒ m( x ) = Lím = ind
tg Δx →0 Δx 1 Δx → 0 Δx 0
(5x − 2)− [5(x + Δx )− 2] 5x − 2 − 5x − 5Δx + 2

m(x 1 ) = Lím
[5(x + Δx )− 2 ](5x − 2) ⇒ m(x ) = Lím [5(x + Δx )− 2 ](5x − 2)
Δx → 0 Δx 1 Δx →0 Δx
− 5Δx −5 −5 −5
m(x ) = Lím ⇒ m(x ) = Lím ⇒ m(1) = ⇒m =
1 Δx →0 Δx[5(x + Δx )− 2 ](5x − 2 ) 1 Δx →0 (5x − 2)(5x − 2) 9 9

1 −5
Ahora la R.tag : y − y = m = ( x − x ) → y − = ( x −1)
1 tg 1 3 9
9 (3y −1) = − 15( x −1) → 27 y − 9 = − 15 x +15 ⇒ 15 x + 27 y − 24 = 0 ⇒ 5 x + 9 y − 8 = 0

5.- Determine una ecuación para cada una de las rectas normales a la
curva y = x 3 − 4 x que sean paralelas a la recta x + 8 y − 8 = 0

( x + Δx)3 − 4(x + Δx) − x3 + 4x 0
Calculamos mtg ⇒ m(x ) = Lím = ind
1 Δx→0 Δx 0
x3 + 3x2Δx + 3x Δx2 + Δx3 − 4x − 4Δx − x3 + 4x
m(x1) = Lím
Δx→0 Δx
Δx ⎡3x2 + 3xΔx + Δx2 − 4⎤
/
3x2Δx + 3xΔx2 + Δx3 − 4Δx ⎢ ⎥
m(x ) = Lím ⇒ m(x ) = Lím ⎣ ⎦
1 Δx→0 Δx 1 Δx→0 //
Δx
m(x ) = Lím3x2 + 3xΔx + Δx2 − 4 ⇒ m(x ) = 3x2 − 4
1 Δx→0 1
−1 −1
m = ⇒m = ( mRN)
n m(x) n 2 −4
3x

13


Como las rectas buscadas son paralelas a la recta dada
igualamos las pendientes
−x + 8 −1
x + 8y − 8 = 0 ⇒ y= ⇒m =
8 8
−1 −1
= ⇒ − 3x 2 + 4 = − 8 ⇒ − 3x 2 + 12 = 0 ⇒ x 2 = 4 ⇒ x = + 2
8 3x 2 − 4 −

sustituir en la ec. de la curva para calcular los valores de y:
y = x 3 − 4x → x=2 ⇒ Punto (2,0); x = − 2 ⇒ Punto ( − 2,0)
−1 −1
Para L1 : Punto (2,0); m = ⇒ y − 0 = ( x − 2) ⇒ x + 8y − 2 = 0
8 8
−1 −1
Para L2 : Punto (−2,0); m = ⇒ y − 0 = ( x + 2) ⇒ x + 8y + 2 = 0
8 8

6.- Encontrar una ecuación para cada una de las rectas tangentes a la
curva 3 y = x 3 − 3 x 2 + 6 x + 4 que sean paralelas a la recta 12 x − 7 y + 2 = 0

⎡( x + Δx)3 4⎤ x3 2 4
− ( x + Δx) + 2( x + Δx) + ⎥ − + x − 2x −
2
⎢
x3 4 ⎢ 3 3⎥ 3 3 0
f(x) = − x2 + 2x + ⇒f′(x) = Lím⎣ ⎦ = Ind
3 3 Δx→0 Δx 0

(x3 + 3x2 Δx + 3xΔx2 + Δx3) x3
− ( x2 + 2xΔx + Δx2 ) + 2x + 2Δx − + x2 − 2x
f′(x) = Lím 3 3
Δx→0 Δx

x3 2 Δx3 2 x3
+ x Δx + xΔx2 + −x − 2xΔx − Δx2 + 2x + 2Δx − + x2 − 2x
f′(x) = Lím 3 3 3
Δx→0 Δx

14


Δx ⎡x2 + xΔx − 2x − Δx + 2 ⎤
//
x2 Δx + xΔx2 − 2xΔx − Δx2 + 2Δx ⎢ ⎥
f ′(x) = Lím ⇒ m(x ) = Lím ⎣ ⎦
Δx→0 Δx 1 Δx→0 Δx /
m(x1) = x2 − 2x + 2 mtg a la curva
sus pendientes son iguales (paralelas) mtg = m
(recta dada)
12
12x − 7y + 2 = 0 ⇒−7y = −12x − 2 → mRD =
7

12
= x2 − 2x + 2 → 12 = 7x2 −14x + 14 ⇒ 7x2 −14x + 2 = 0
7

( −14) ± ( −14)2 − 4 ( 7)( 2) 14 ±12
x=− ⇒ x=
2 ( 7) 14
14 +12 26 14 −12 2 1
x = → x = → x = 2; x = → x = → x =
1 14 1 14 1 2 14 2 14 2 7
Sust los valores de x en la curva para x = 2

23 4 8 4 8 4
y= − ( 2)2 + ( 2)2 + → y = − 4 + 4 + ⇒y = + → y=4 Punto (2,4)
3 3 3 3 3 3
3 1
⎛1⎞
⎜ ⎟ 2 3
1 ⎛1⎞ ⎛1⎞ 4 1 2 4
Para x = ⇒ y = ⎝ ⎠ − ⎜ ⎟ + 2⎜ ⎟ +
7
→ y= 7 − + +
7 3 ⎝7⎠ ⎝7⎠ 3 3 72 7 3
1 1 2 4 1 − 21 + 1666 1646
y= − + + → y= → y= ⇒ y = 1,59 ≅ y = 1,6
3( 7)3 49 7 3 1029 1029
Las ecuaciones son:

1 tg (
1 )
y − y = m x − x ⇒ Para L :
1
m=
12
7
Punto (2,4) ⇒ y − 4 =
12
7
( x − 2) ⇒12x − 7y + 4 = 0
12 ⎛1 ⎞
Para L : m= Punto ⎜ , 1.6⎟
2 7 ⎝7 ⎠
12 ⎛ 1⎞
y − 1.6 = ⎜x − ⎟ → 7 y −11.2 = 12x − 0.14⇒ 12x − 7 y +11.06 = 0
7⎝ 7⎠

15


7.- Hallar el ángulo determinado por la tangente a la curva y = x 3 en el punto
3
x =
3
2
(x + Δx) 3 − x 3 0 x 3 + 3x Δx + 3x Δx 2 + Δx 3 − x 3
m(x ) = Lím = ind ⇒ m(x ) = Lím
1 Δx → 0 Δx 0 1 Δx → 0 Δx
Δx ⎢⎡3x 2 + 3x Δx + Δx 2 ⎤
2 /
3x Δx + 3x Δx 2 + Δx 3 ⎣ ⎥
⎦
1 Δx → 0 Δx 1 Δx → 0 Δx/
2
2 ⎛ 3⎞ ⎛ 3⎞ ⎛ 3⎞
m(x ) = 3x sus t ⇒ m ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ 3 ⎟ = 3⎜ 3 ⎟ ⇒ m ⎜ 3 ⎟ = 1 ⇒ m sec = tg θ ⇒ tg θ = 1 ⇒ θ = 45 °
1
⎝ ⎠ ⎝ ⎠ ⎝ ⎠

8.- Determinar los parámetros “a”, “b” y “c” en la ecuación de la parábola
y = ax 2 + bx + c de tal manera que la recta y = x sea tangente a ella en x = 1 y
dicha curva pase por el punto (-1, 0).

a(x + Δx) 2 + b (x + Δx) + c − ⎡ ax 2 + bx + c ⎤
⎢
⎣ ⎥ 0
⎦ = ind
m(x ) = Lím
1 Δx → 0 Δx 0
ax 2 + 2ax Δx + a Δ x 2 + bx + b ΔΔ + c − ax 2 − bx − c
m(x ) = Lím
1 Δx → 0 Δx
2ax Δx + a Δ x 2 + b ΔΔ Δx [2ax + a Δ x + b ]
1 Δx → 0 Δx 1 Δx → 0 Δx
m(x ) = 2ax + b m tg
1
R tg y = x es tg a la parábola en x = 1 ⇒ p tg (1,1)
Sust : m(1) = 2a + b de la ec. de la recta y=x ⇒ m =1
1 = 2a + b → 2a + b = 1 Ec (1)
Sust el p tg en la parábola ⇒ y = ax 2 + bx + c ⇒ a + b + c = 1 Ec( 2)
la parábola pasa por ( − 1, 0) ⇒ y = ax 2 + bx + c → a − b + c = 0 Ec( 3)
Tenemos tres ecuaciones :
1) 2a + b = 1 2) a + b + c = 1 3) a − b + c = 0
1
a + c + b =1 ⇒ b + b =1 ⇒ b =
2
1 1
2a + 1 → a=
2 4
1
a+ c =b → c =b − a → c =
4

16


El proceso de calcular la derivada de una función en forma directa a
partir de su definición, puede consumir mucho tiempo y ser tedioso. Esta sección
contiene reglas que simplifican la tarea de encontrar derivadas de las funciones
más complicadas en forma casi instantánea.

Notaciones para la derivada.
Cuando y = f (x ) se utilizan las siguientes notaciones para las derivadas.

f ´(x) = Dx [ f ( x)] = d x y = y´= dy / dx = d / dx[ f ( x)]
Todas las notaciones anteriores se utilizan en las matemáticas y sus
aplicaciones, es recomendable que el lector se familiarice con ellas.
El subíndice x en el símbolo Dx y se utiliza para designar a la variable
independiente, y Dx para derivar la función.

Teoremas para Determinar Derivadas.
Sea f ' (u ) el símbolo para denotar derivadas, podemos enunciar los
siguientes teoremas. (No se demostrará ninguno de los teoremas, ya que no es
objetivo de este trabajo).
A.- Teoremas Fundamentales de funciones Algebraicas.
Teorema 1: Derivada de una constante. f (u ) = a ⇒ f ' (u ) = 0

Teorema 2: Derivada de una variable. f (u ) = u ⇒ f ' (u ) = 1

Teorema 3: Derivada de la potencia de una Variable. f (u ) = u n ⇒ f ' (u ) = nu n − 1

Teorema 4: Derivada para la suma algebraica de funciones.
f (u ) = F (u ) ± G (u ) ⇒ f ' (u ) = F ' (u ) ± G ' (u )
Teorema 5: Derivada del producto de dos funciones
f (u ) = F (u ) G (u ) ⇒ f ' (u ) = F ' (u ) G (u ) + F (u ) G ' (u )
Teorema 6: Derivada de un cociente de funciones.
F (u ) F ' (u ) G (u ) − F (u ) G ' (u )
f (u ) = ⇒ f ' (u ) = , G (u) ≠ 0.
G (u ) G (u ) 2
Teorema 7: Derivada de una función Compuesta. Sea y = f (u ) y u = g ( x )
que determinan una función compuesta y = f ( g ( x )). Si g es diferenciable en x y
ƒ es diferenciable en u = g (x ) , entonces: Dx y = Dx y Dx u

17


Una de las aplicaciones principales del teorema anterior es para desarrollar otras
fórmulas de derivación, por ejemplo:
Regla de la potencia para funciones.

f (u ) = [ F (u )]n ⇒ f ' (u ) = n[ F (u )]F ' (u )
B.- Teoremas de funciones trascendentales.

a.- Teoremas de las funciones Exponenciales y Logarítmicas.

Teorema 8: Derivada de la función logaritmo natural. F(u) > 0
F ' (u )
f (u ) = Ln[ F (u )] ⇒ f ' (u ) =
F (u )
Teorema 9: Derivada de la función logaritmo de base a de u.

F ' (u )
f (u ) = Log [ F (u )] ⇒ f ' (u ) = , para u =F(u) ≠ 0, ( a > 0 , a ≠ 1)
a F (u ) Ln ( a )

Teorema 10: Derivada para las funciones logaritmo y exponencial generales.
F (u ) F (u )
f (u ) = a ⇒ f ' (u ) = a Ln(a) F ' (u ) (a>0)

Teorema 11: Regla para la función exponencial natural.
F (u ) F (u )
f (u ) = e ⇒ f ' (u ) = e F ' (u )

b.- Teoremas Trigonométricos para la Derivación.
A continuación se presentan las derivadas de las seis funciones
trigonométricas. En el enunciado de los teoremas se supone que u = g (x ), donde
g es una función derivable y x se restringe a los valores para los que la función
trigonométrica está definida.
Teorema 12: Derivada de la función seno.
f (u ) = Sen[F (u )] → f ´(u ) = (cos u ) F´(u )
Teorema 13: Derivada de la función coseno.
f (u ) = Cos[F (u )] → f ´(u ) = ( Sen u ) F´(u )
Teorema 14: Derivada de la función tangente.
f (u ) = Tag [F (u )] → f ´(u ) = ( Sec 2 u ) F ´(u )

18


Teorema 15: Derivada de la función cosecante.
f (u ) = Csc[F (u )] → f ´(u ) = −(Csc u )(Ctg u ) F´(u )
Teorema 16: Derivada de la función secante.
f (u ) = Sec[F (u )] → f ´(u ) = ( Sec u ) (tg u ) F´(u )
Teorema 17: Derivada de la función cotangente.
f (u ) = Ctg [F (u )] → f ´(u ) = (Csc 2u ) F´(u )

c.- Teoremas Trigonométricos Inversos sobre la Derivación.
En los teoremas siguientes se supone que u = g(x), donde g es una
función derivable y x se restringe a los valores para los que las expresiones
indicadas tienen sentido.
Teorema 18: Derivada para la función arco seno.
F´(u )
f (u ) = Arc Sen[F (u )] → f ´(u ) =
1 − [F (u )]
2

Teorema 19: Derivada para la función arco coseno.
− F´(u )
f (u ) = Arc Cos[F (u )] → f ´(u ) =
1 − [F (u )]
2

Teorema 20: Derivada para la función arco tangente.
F´( u )
f (u ) = Arc Tg [F (u ) ] → f´( u ) =
1 + [F (u ) ]
2

Teorema 21: Regla para la función arco cotangente.
− F ´(u )
f (u ) = Arc Ctg [F (u )] → f ´(u ) =
1 + [F (u )]
2

Teorema 22: Derivada para la función arco secante.
F´(u )
f (u ) = Arc Sec[F (u )] → f ´(u ) =
F (u ) [F (u )] −1
2

Teorema 23: Derivada para la función arco cosecante.
− F´(u )
f (u ) = Arc Csc[F (u )] → f ´(u ) =
F (u ) [F (u )] −1
2

19


Derivar y Simplificar
a) Funciones Algebraicas
1 4 1
1− . y = + = x − 2 + 4 x − 1/2
2x 2 x 2

dy ⎛ 1⎞ ⎛ 1 2 ⎞
= − x − 3 + 4 ⎜ − ⎟ x −3/2 = − ⎜ + ⎟
dx ⎝ 2⎠ ⎜ x3 ⎟
⎝ x3 ⎠

( ) ( )( ) ( )( )
4 3 3
2 − . f ( x ) = 3x − x 3 + 1 ; f´ ( x ) = 4 3x − x 3 + 1 3 − 3 x 2 = 12 3x − x 3 + 1 1 − x2

( )
1 −1/2 2−x
3−. y = 3 + 4x − x 2 ; y´ = 3 + 4x − x 2 ( 4 − 2x ) ⇒ f ´( x ) =
2
3 + 4x − x 2
3 r + 2 d θ (2r + 3)3 − (3r + 2)2 6r + 9 − 6r − 4 5
4 −. θ = ; = 2
→ ⇒ θ ´( r ) =
2
2r + 3 dr (2r + 3) ( 2 r + 3) ( 2 r + 3 )2
5
⎛ x ⎞
5−. y = ⎜ ;y=
x5
; y´ =
(1 + x )5 . 5 x 4 − x 5 (1 + x )4 . 5
⎟
⎝1 + x ⎠ (1 + x )5 (1 + x )10

y´ =
(1 + x )4 . 5 x 4 (1 + x − x)
=
5 x4
(1 + x )10 (1 + x )6
6 − . y = ( x − 1) x 2 − 2 x + 2 ; y´ = x2 − 2 x + 2 +
(x − 1) ( 2x − 2 )

2 x 2 − 2x + 2

y´ = x2 − 2 x + 2 +
(x − 1) 2
=
( x 2 − 2 x + 2 ) + ( x − 1)2 = 2 x 2 − 4x + 3
x2 − 2 x + 2 x 2 − 2x + 2 x 2 − 2x + 2

( )
− 1/2
1 − 4 w 2 − w (1/2 ) 1 − 4 w 2 ( −8 w )
w dz
7 −. z = ; = =
1 − 4 w2
dw 1 − 4 w2

4 w2
1 − 4 w2 +
=
1 − 4 w2
=
(1 − 4 w 2 ) + 4 w 2 = 1
1 − 4 w2 1 − 4 w 2 (1 − 4 w 2 )
(1 − 4 w 2 )
3

x +1 x −1 (x + 1) − ( x − 1)
−
x −1 2 x −1 2 x +1 2 (x − 1)( x + 1)
8 − . f (x) = ; f ´(x) = =
x +1 x +1 x +1
x +1− x +1 1
f ´(x) = =
2 ( x + 1) x 2 − 1 ( x + 1) x 2 − 1

20


9 − . y = ( x2 + 3)
( 2x − 5) ; y´ = 4( x + 3) 2x ( 2x − 5) + 3( 6 x) ( 2x − 5) ( x2 + 3)
4 3 3 2 3 3 3 2 3 2 4

y´= 2x ( 2x − 5) ( x + 3) ⎡4 ( 2x − 5) + 9( x + 3)⎤
3 2 2 3 3 2
⎣ ⎦
y ´ = 2x ( 2x − 5) ( x + 3) (17x + 27x − 20)
3 2 2 3 3

10. − f(x) = x(x −1)2 (x − 2)3
f´(x) = (x −1)2 (x − 2)3 + 2x(x −1)(x − 2)3 + 3x(x −1)2 (x − 2)2
f´(x) = (x −1)(x − 2)2 [ (x −1)(x − 2) + 2x(x − 2) + 3x(x −1)]
f´(x) = (x −1)(x − 2)2 ⎡6x2 −10x + 2⎤ ⇒ f´(x) = 2(x −1)(x − 2)2 ⎡3x2 − 5x +1⎤
⎣ ⎦ ⎣ ⎦
x3 3x2 (x2 + 3) − x2 (2x) x2 (x2 + 9)
11. − f(x) = ⇒ f´(x) = ⇒ f´(x) = 2
x2 + 3 (x2 + 3)2 (x + 3)2
4x 4(x2 + 4) − 4x(2x) 4(4 − x2 )
12. − f(x) = ⇒ f´(x) = ⇒ f(x) = 2
x2 + 4 (x2 + 4)2 x +4
13. − f(x) = x 4 − x2
x
f´(x) = 4 − x2 + (4 − x2 )−1 2 ( − 2x) ⇒ f´x) = (4 − x2 )−1 2 ⎡4 − x2 − x2 ⎤ ⇒ f´x) = 2(4 − x2 )−1 2 ⎡2 − x2 ⎤
⎣ ⎦ ⎣ ⎦
2
2 ⎡2 − x2 ⎤
f´x) = ⎣ ⎦
4−x 2

14. − f(x) = 10x3 (x −1)2
f´(x) = 30x2 (x −1)2 + 20x3 (x −1) ⇒ f´(x) = 10x3 (x −1)(5x − 3)

15. − f(x) = (x − 2)3 (x +1)4
f´(x) = 3(x − 2)2 (x +1)4 + 4(x − 2)3 (x +1)3 ⇒ f´(x) = (x − 2)2 (x +1)3 [3(x +1) + 4(x − 2)]
f´(x) = (x − 2)2 (x +1)3 [3x + 3 + 4x − 8)] ⇒ f´(x) = (x − 2)2 (x +1)3 [ 7x − 5]

2x2
16. − f(x) =
9 − x2
4x(9 − x2 ) − 2x2 ( − 2x) 4x(9 − x2 + x2 ) 36x
f´(x) = ⇒ f´(x) = ⇒ f´(x) =
(9 − x )
2 2
(9 − x )
2 2
(9 − x2 )2

36x
17. − f(x) =
(9 − x2 )2
36(9 − x2 )2 − 36x ⎡−4x(9 − x2 )⎤
⎣ ⎦ 36(9 − x2 ) ⎡9 − x2 + 4x2 ⎤
⎣ ⎦ 108 ⎡3 + x2 ⎤
⎣ ⎦
f´(x) = ⇒ f´(x) = ⇒ f´(x) =
(9 − x2 )4 (9 − x2 )4 (9 − x2 )3

21


x 2 − 2x + 2
18. − f(x) =
x −1
(2x − 2)(x − 1) − (x 2 − 2x + 2) (2x − 2)(x − 1) − (x 2 − 2x + 2) x(x − 2)
f´(x) = ⇒ f´(x) = ⇒ f´(x) =
(x − 1) 2
(x − 1) 2
(x − 1)2
x 2 − 2x
19. − f(x) =
(x − 1)2
(2x − 2)(x − 1)2 − 2(x 2 − 2x)(x − 1)3 2(x − 1)3 − 2(x 2 − 2x)(x − 1)
f´(x) = ⇒ f´(x) =
(x − 1)4 (x − 1)4
2(x − 1) ⎡(x − 1)2 − (x 2 − 2x) ⎤
⎣ ⎦ 2
f´(x) = ⇒ f´(x) =
(x − 1)4 (x − 1)3
x 2 − 2x
20. − f(x) =
(x − 1)2
(2x − 2)(x − 1)2 − 2(x 2 − 2x)(x − 1)3 2(x − 1)3 − 2(x 2 − 2x)(x − 1)
f´(x) = ⇒ f´(x) =
(x − 1) 4
(x − 1)4
2(x − 1) ⎡(x − 1)2 − (x 2 − 2x) ⎤
⎣ ⎦ 2
f´(x) = ⇒ f´(x) =
(x − 1) 4
(x − 1)3
2 + x − x2
21. − f(x) =
(x − 1)2
(1 − 2x)(x − 1)2 − 2(2 + x − x 2 )(x − 1) (x − 1) ⎡(1 − 2x)(x − 1) − 2(2 + x − x 2 ) ⎤
⎣ ⎦
f´(x) = ⇒ f´(x) =
(x − 1)4 (x − 1)4
⎡(1 − 2x)(x − 1) − 2(2 + x − x 2 ) ⎤
⎦ ⇒ f´(x) = x − 5
f´(x) = ⎣
(x − 1)3 (x − 1)3
(x − 1)2 (x + 2)
22. − f(x)
x3
(3x 2 − 3)x 3 − (x 3 − 3x + 2)3x 2 3x 2 ⎡(x 2 − 1)x − (x 3 − 3x + 2⎤
⎣ ⎦
f´(x) = ⇒ f´(x) =
x6 x6
⎡ ⎤
3 ⎣ x 3 − x − x 3 + 3x − 2⎦ 6 [ x − 1]
f´(x) = 4
⇒ f´(x) =
x x4
(x − 1) 2
23. − f(x) =
x +1
2(x − 1)(x + 1) − (x − 1)2 (x − 1) [ 2(x + 1) − (x − 1)] (x − 1) [ x + 3]
f´(x) = ⇒ f´(x) = ⇒ f´(x) =
(x + 1) 2
(x + 1) 2
(x + 1)2
(x − 1)(x + 3) 2(x + 1)(x + 1)2 − 2(x 2 + 2x − 3)(x + 1)
24. − f(x) = ⇒ f´(x) = ⇒
(x + 1) 2
(x + 1)4
2(x + 1) ⎡ x 2 + 2x + 1 − x 2 − 2x + 3⎤
⎣ ⎦ 2 [ 4]
f´(x) = ⇒ f´(x) =
(x + 1) 4
(x + 1)3

22


−1/2 ⎡
1 − x ) − (1 + x )( −1) ⎤
25. − F(x) =
1+ x 1 ⎛1 + x ⎞
⇒ f´(x) = ⎜ ⎟ ⎢( ⎥
1 −x 2 ⎝1 − x ⎠ ⎢ 2 ⎥
⎣ (1 − x ) ⎦
−1/2 ⎡ ⎤ −1/2 ⎡ ⎤
1 ⎛1 + x ⎞ ⎛ ⎞
⎢1 − x + 1 + x ⎥ ⇒ f´(x) = 1 ⎜ 1 + x ⎟ ⎢ /
2 ⎥
f´(x) = ⎜ ⎟
2 ⎝1 − x ⎠ ⎢ (1 − x )2 ⎥ /
2 ⎝1 − x ⎠ ⎢ (1 − x )2 ⎥
⎣ ⎦ ⎣ ⎦
−1/2
1 ⎛1 + x ⎞ 1 1 1
f´(x) = ⎜ ⎟ ⇒ f´(x) = ⇒ f´(x) =
/
2 ⎝1 − x ⎠ (1 − x )2 1+ x /
(1 − x )4 (1 + x ) (1 − x )3
1− x
x
(x 2 + 3) 2 − (x 2 + 3) − 2 2x
1 1

x 2
26. − f(x) = ⇒ f´(x) =
x2 − 3 (x 2 + 3)
(x 2 + 3) − 2 ⎡ x 2 + 3 − x 2 ⎤
1

⎣ ⎦ ⇒ f´(x) = 3
f´(x) =
(x + 3)
2
(x + 3)3
2

2x 2 4x(x 2 − x − 2) − 2x 2 (2x − 1) −2x(x + 4)
27. − f(x) = ⇒ f´(x) = ⇒ f´(x) = 2
x2 − x − 2 (x 2 − x − 2) 2 (x − x − 2) 2
x 2 − 3x + 2 (2x − 3)(x 2 + 2x + 1) − (x 2 − 3x + 2)(2x + 2)
28. − f(x) = ⇒ f´(x) =
x + 2x + 1
2
(x 2 + 2x + 1)2
2x 3 + 4x 2 + 2x − 3x 2 − 6x − 3 − 2x 3 + 6x 2 − 4x − 2x 2 + 6x − 4
f´(x) =
(x 2 + 2x + 1) 2
4x 2 + 2x − 3x 2 − 3 + 6x 2 − 4x − 2x 2 − 4 5x 2 − 2x − 7
f´(x) = ⇒ f´(x) = 2
(x 2 + 2x + 1) 2 (x + 2x + 1) 2
x2 +1
29. − f(x) =
x2 −1
2x 2
2x(x 2 − 1) 2 − (x 2 + 1)(x − 1) − 2
1 1

x(x 2 − 1)− 2 ⎡ 2(x 2 − 1) − (x 2 + 1) ⎤
1

f´(x) = 2 ⇒ f´(x) = ⎣ ⎦
x −1
2
x −1
2

x ⎡ 2x − 2 − x − 1⎤
2 2
⎦ ⇒ f´(x) = x(x − 3)
2
f´(x) = ⎣
(x − 1)
2 3
(x 2 − 1)3

30. − F(x) =
(1 − 2x ) ( 3x + 2 ) ⇒ F(x) =
3x + 2 − 6x 2 − 4x
⇒ F(x) =
(
−6x 2 − x + 2 )
( 5x − 4 ) ( 5x − 4 ) ( 5x − 4 )

F´(x) =
( −12x − 1)( 5x − 4 ) − ( −6x2 − x + 2) (5)
( 5x − 4 )2
6 ⎡ −5x 2 + 8x −1⎤
−60x 2 + 48x − 5x + 4 + 30x 2 + 5x −10 −30x 2 + 48x − 6 ⎢ ⎥
F´(x) = ⇒ F´(x) = ⇒ F´(x) = ⎣ ⎦
2 2 2
5x − 4( ) 5x − 4 ( ) 5x − 4 ( )
23


1 + x2
31. − y = 3
1 − x2
−2/3 ⎡ 2x (1 − x2 ) − (1 + x2 ) ( −2x ) ⎤ 2 −2/3 ⎡ ⎤
1 ⎡1 + x2 ⎤ ⎢ ⎥ ⇒ y´ = 1 ⎡1 + x ⎤ ⎢ 4x ⎥
y´ = ⎢
3 ⎣ 1 − x2 ⎥
⎦ ⎢ (1 − x2 )
2
⎥ 3 ⎢ 1 − x2 ⎥ ⎢ (1− x2 )2 ⎥
⎣ ⎦ ⎣
⎣ ⎦ ⎦
4x 4x
y´ = ⇒ y´ =
2 2
⎛ 1 + x2 ⎞ ⎛ 1 + x2 ⎞
3 (1− x ) 3 ⎜ 2 ⎟ (1− x2 )
2 2 6
⎜ 2 ⎟
3

⎝1 − x ⎠ ⎝1 − x ⎠
4x 4x
y´ = ⇒ y´ =
(1 + x ) 1 − x 2 2
3 3 (1 + x2 ) (1 − x2 )
2 4

3 3 ( ) 2 6

(1 − x ) 2 2

2x
32. − y =
x +1
1/2 −1/2 ⎡ 2 ( x + 1) − 2x (1) ⎤
2x ⎛ 2x ⎞ 1 ⎛ 2x ⎞
y= ⇒ y=⎜ ⎟ → y´ = ⎜ ⎟ ⎢ ⎥
x +1 ⎝ x + 1⎠ 2 ⎝ x + 1⎠ ⎢
⎣ ( x + 1)2 ⎥
⎦
⎡ ⎤
y´ = ⎢ 2x + 2 − 2x ⎥ ⇒ y´ = 1
1 1
→ y´ =
1
1/2 ⎢ x + 1 2 ⎥ 2
⎛ 2x ⎞ ⎣ ( ) ⎦ 2x ( x +1) 2x ( x + 1)3
2⎜ ⎟ x +1
⎝ x + 1⎠

2x2 − 1 2x2 − 1 2x2 − 1
33. − y = ⇒y = ⇒ y=
x 1 + x2
( ) (
x2 1 + x2 ) x2 + x4
1/2

4x ( x2 + x4 ) − ( 2x2 − 1) 1 ( x2 + x4 ) ( 2x + 4x3 )
1/2 −1/2

2
y´ =
(x )
2 + x4

( x2 + x4 ) ⎡⎢⎣4x ( x2 + x4 ) − ( 2x2 − 1)( x + 2x3)⎤⎥⎦ ⇒ y' = 4x + 4x − 2x − 4x + x + 2x
−1/2

3 5 3 5 3
y' =
( x2 + x 4 ) ( x 2 + x4 )
3

4x3 + x x ( 4x2 −1)
y' = → y' =
(x + x4 ) (x + x4 )
2 3 2 3

24


⎡1 ⎞⎤
1+ x 2
⎛ 1
− 1/2 ⎢ x − 1/2 1 − x − 1 + x ⎜ − x − 1/2 ⎟ ⎥
1 ⎛1 + ⎝ 2 x⎞ ⎠⎥
( ) ( )
34)F(x) = ⎢
⇒ y´ = ⎜ ⎟
⎜ ⎟
( )
1− x ⎢2 ⎝1 − 2 x⎠ ⎥
1− x
⎢
⎣ ⎥
⎦

1
⎡ 1 − 1/2 ⎡
⎢2x ⎣
1 − x + 1 + x ⎤⎥
⎦
⎤
( ) ( )
y´ = ⎢ ⎥
( )
1+ x ⎢ 2
2 1− x ⎥
⎣ ⎦
1− x
⎡ 1 − 1/2 ⎤ ⎡ ⎤
⎢2x ⎢ x − 1/2 ⎥
(2) ⎥
1 1
y´ = ⎢ ⎥ → y´ = ⎢ 2⎥
( ) ( )
1+ x 2 1+ x
2 ⎢ 1− x ⎥ 2 ⎢ 1− x ⎥
⎣ ⎦ ⎣ ⎦
1− x 1− x
⎡ ⎤
1 ⎢ 1 ⎥ 1 1
y´ = ⎢ ⇒ y´ = ⇒ y´ =
2⎥
2
1+ x ⎢ x1/2 1 − x ⎥
⎣ ⎦ ( 2x1/2 ) 1+ x
(1 − x )
4
2 x (1 + x ) (1 − x )
3
1− x (1 − x )
x ( − 2 x ) (π 2 − x 2 )
− 1/ 2
π2 ⎛1⎞
35) y = x π − x ⇒ y ' = (π − x
2 2 2
)
2 1/ 2
+ + ⎜ ⎟
2 x ⎝π ⎠
2
1−
π2
π
y ' = (π 2 − x 2 ) − x 2 (π 2 − x 2 ) ⇒ y ' = (π 2 − x 2 ) − x 2 (π 2 − x 2 ) + π 2 (π 2 − x 2 )
1/ 2 − 1/ 2 1/ 2 − 1/ 2 − 1/ 2
+
π 2 − x2
π
y ' = (π 2 − x 2 ) ⎡ (π 2 − x 2 ) − x 2 + π 2 ⎤ ⇒ y ' = (π 2 − x 2 )
− 1/ 2 − 1/ 2
⎡π 2 − x 2 − x 2 + π 2 ⎤
⎣ ⎦
⎣ ⎦
y ' = (π 2 − x 2 ) 2 (π 2 − x 2 ) ⇒ y `= 2 π 2 − x 2
− 1/ 2

36) f ( x ) = x 2 − 4

Re cordar que : a = a 2 ⇒ f ( x ) = ( x 2 − 4) 2 ⇒ f ( x ) = (( x 2 − 4) 2 )
1
2

1 1
f ´( x ) = (( x 2 − 4) 2 ) − 2 (( x 2 − 4) 2 )′ ⇒ f ´( x ) = (( x 2 − 4) 2 ) − 2 (2( x 2 − 4)2 x )
1 1

2 2
2 x ( x 2 − 4) 2 x ( x 2 − 4)
f ´( x ) = ⇒ f ´( x ) =
( x 2 − 4)2 x2 − 4
3
37)f(x) = x
1 2 −1 2
f(x) = ( x 2 ) 3 ⇒ f´(x) = 3( x 2 ) 2 ( x 2 )´ ⇒ f´(x) = 3( x 2 ) 2 (x ) 2x
2
2
3x( x 2 ) 2 3x x
f´(x) = ⇒ f´(x) = ⇒ f´(x) = 3x x
( x2 ) x

25


b. Funciones Trigonométricas.
38)y = Sen (3x) + Cos (2x) ⇒ y´ = 3 cos (3x) − 2 Sen (2x)
39) y = tan 2 (x 2 ) ⇒ y´ = 2 tan (x 2 )Sec2 (x 2 ) 2x
40)y = Cot (1 − 2 x 2 ) ⇒ y´ = − Csc 2 (1 − 2 x 2 ) ( −4x ) ⇒ 4x Cosec2 (1 − 2 x 2 )
2 2 ⎛ 2 ⎞ 2 2
41)y = Sen ( ) ⇒ y´ = Cos ( ) ⎜ − 2 ⎟ y´= − 2 Cos ( )
x x ⎝ x ⎠ x x
42)y = Cos 2 (1 − x 2 ) ⇒ y´ = 2 Cos (1 − x 2 ) ⎡ − Sen (1 − x 2 ) ⎤ ( −2x ) ⇒ y´ = 2xSen 2 (1 − x 2 )
⎣ ⎦
43)y = Sen ( 2x − 3) ⇒ y´ = 3sen ( 2x − 3) Cos ( 2x − 3) 2x ⇒ y´ = 3xsen2 ( 2x − 3) Sen ( 2x − 3)
3 2

1 1
44)y = Sec2 ( x 2 − 1) ⇒ y´ = 2( )Sec ( x 2 −1) sec ( x 2 −1) tan ( x 2 −1) 2x
2 2
2xSen ( x 2 − 1)
y´ = 2x sec2 ( x 2 −1) tan ( x 2 −1) ⇒ y´=
Cos3 ( x 2 − 1)
1/2
1 dz -3/2 ( Sec (2w) −1) Sec (2w)tan (2w) 2
45)z ( w) = ⇒ =
(Sec (2w) −1)3/2 dw (Sec (2w) −1)3
dz -3 Sec(2w)tan (2w)
=
dw ( Sec(2w) −1)5/2
46).y =
Senx + Cosx
⇒ y' =
( Cosx − Senx )( Senx − Cosx ) − (Senx + Cosx )( Cosx + Senx )
Senx − Cosx ( Senx − Cosx )2
− ( Senx − Cosx )( Senx − Cosx ) − ( Senx + Cosx )2 − ⎡( Senx − Cosx )2 + ( Senx + Cosx )2 ⎤
⎢ ⎥
y' = ⇒ y' = ⎣ ⎦
2 2
(
Senx − Cosx ) (
Senx − Cosx )
⎡Sen 2 x − 2Senx Cosx + Cos2 x + Sen 2 x + 2Senx Cosx + Cos 2 x ⎤
⎢
⎣ ⎥
⎦
y' = −
2
(
Senx − Cosx )
− ⎡ 2(Sen x + Cos x) ⎦
2
⎤ 2
−2
y' = ⎣ → y' =
[Senx − Cosx ] [Senx − Cosx ]
2 2

47)y = 3Senx Cos 2 x + Sen 3 x
y' = 3 ⎡Cosx Cos 2 x + 2SenxCosx( − Senx) ⎤ + 3Sen 2 x Cosx
⎣ ⎦
y' = 3Cos3 x − 6Sen 2 x Cosx + 3Sen 2 x Cosx ⇒ y' = 3Cos3 x − 3Sen 2 x Cosx
y' = 3Cosx ⎡Cos 2 x − Sen 2 x ⎤ ⇒ y' = 3Cosx Cos(2x)
⎣ ⎦

26


1 1
48)y = 3 Sen 2 x + 3
⇒ y = (Sen 2 x)1/3 + ⇒ y = (Sen 2 x)1/3 + Cos−3x
Cos x Cos3x
1 2Senx Cosx 3Senx
y' = (Sen 2 x)2/3 2Senx Cosx + ⎡−3Cos−4 x ( − Senx)⎤ ⇒ y' =
⎣ ⎦ + 4
3 3Senx 3 (Sen x) Cos x
2 2

2Cosx 3Senx
y' = + 4
3 3 Senx Cos x

49)y = 3Senx Cos2 x + Sen3x
y' = 3 ⎡Cosx Cos2 x + 2SenxCosx( − Senx) ⎤ + 3Sen 2 x Cosx
⎣ ⎦
y' = 3Cos3x − 6Sen 2 x Cosx + 3Sen 2 x Cosx ⇒ y' = 3Cos3x − 3Sen 2 x Cosx
y' = 3Cosx ⎡Cos2 x − Sen 2 x ⎤ ⇒ y' = 3Cosx Cos(2x)
⎣ ⎦

Cosx 4
50)y =− + Ctgx
3Sen3x 3
−1 ⎡ −Senx(Sen3x) − 3CosxSen 2 x Cosx ⎤ 4 1 ⎡ −Sen 4 x − 3Cos2 xSen 2 x ⎤ 4
y' = − (Csc 2 x) ⇒ y' =− ⎢ ⎥ − 3 Csc x
2

3⎢ ⎣ (Sen3x)2 ⎥ 3
⎦ 3⎣ Sen6 x ⎦
1 Sen 2 x(Sen 2 x + 3Cos2 x) 4 1 Sen 2 x + 3Cos2 x 4
y' = 6
− 2
⇒ y' = 4
−
3 Sen x 3Sen x 3 Sen x 3Sen 2 x
1 ⎡ Sen 2 x + 3Cos2 x − 4Sen 2 x ⎤ 1 ⎡ −3Sen 2 x + 3Cos2 x ⎤ Cos2x
y' = ⎢ 4 ⎥ ⇒ y' = ⎢ 4 ⎥ ⇒ y' = Sen 4 x
3⎣ Sen x ⎦ 3⎣ Sen x ⎦

1 + Cos(2x)
51). − y =
1 − Cos(2x)
−2Senx (2x) [1 − Cos(2x)] − [1 + Cos(2x)] 2Senx (2x)
y' =
[1− Cos(2x)]
2

−2Senx (2x) [1 − Cos(2x) + 1 + Cos(2x ] −4Senx (2x)
y' = ⇒ y' =
[1 − Cos(2x)] [1 − Cos(2x)]
2 2

1 − Cos 2x 1 + Cos 2x
Sen(2x) = 2CosxSenx;Cos(2x) = Cos2 x − Sen 2 x; Senx = ;Cosx =
2 2
−4[ 2CosxSenx] −4[ 2CosxSenx ] −2Cosx
y' = 2
⇒ y' = 4
⇒ y' =
⎡2Sen x ⎤
2 4Sen x Sen3x
⎣ ⎦

27


⎛a⎞
52)y = Sen (x 2 − 5x + 1) + Tg ⎜ ⎟
⎝x⎠
⎛ ⎛ a ⎞⎞⎛ a ⎞ ⎛ a ⎞ ⎛a⎞
y' = Cos (x 2 − 5x + 1) (2x − 5) + ⎜ Sec 2 ⎜ ⎟ ⎟ ⎜ − 2 ⎟ ⇒ y' = (2x − 5) Cos (x 2 − 5x + 1) − ⎜ 2 ⎟ Sec 2 ⎜ ⎟
⎝ ⎝ x ⎠⎠⎝ x ⎠ ⎝x ⎠ ⎝x⎠

53) F ( x) = α Sen 2 ( β x) + β Cos 2 ( β x)
2 α Sen ( β x) Cos ( β x) + 2 β 2Cos ( β x)(− Sen β x) 2 β Sen ( β x) Cos( β x) [α − β ]
F´( x) = ⇒ F '( x) =
2 α Sen β x + β Cos β x
2 2
2 α Sen 2 ( β x) + β Cos 2 ( β x)
β (α − β ) Sen 2( β x)
Pero :2 Cos β x Sen β x = Sen 2( β x) ⇒ F '( x) =
2 α Sen 2 ( β x) + β Cos 2 ( β x)
⎡ ⎛ S en ( x 2 ) ⎞ ⎤
5 4 ) y = S en 3 ⎢ x 2 + S en ⎜ x 2 + ⎟⎥
⎢ ⎜ x3 ⎟⎥
⎣ ⎝ ⎠⎦
⎡ ⎛ S en ( x ) ⎞ ⎤
2 ⎡ ⎛ S en ( x 2 ) ⎞ ⎤
y ′ = 3 S en ⎢ x + S en ⎜ x +
2 2 2
⎟ ⎥ C o s ⎢ x + S en ⎜ x +
2 2
⎟⎥
⎢ ⎜ x3 ⎟⎥ ⎢ ⎜ x3 ⎟⎥
⎣ ⎝ ⎠⎦ ⎣ ⎝ ⎠⎦
⎡ ⎛ S en ( x 2 ) ⎞ ⎤ ⎡ ( C o s( x 2 ) ) (2 x ) x 3 − (S en (x 2 ) ) 3 x 2 ⎤
⎢2x + C os ⎜ x 2 + ⎟⎥ ⎢2x + ⎥
⎢ ⎜ x3 ⎟⎥ ⎢ x6 ⎥
⎣ ⎝ ⎠⎦ ⎣ ⎦
⎡ ⎛ S en (x 2 ) ⎞ ⎤ ⎡ ⎛ S en (x 2 ) ⎞ ⎤
y ′ = 3 S en 2 ⎢ x 2 + S en ⎜ x 2 + ⎟⎥ C o s ⎢ x 2 + S en ⎜ x 2 + ⎟⎥
⎣ ⎝ x3 ⎠⎦ ⎣ ⎝ x3 ⎠⎦
⎛ x ´6 + S en (x 2 ) ⎞ ⎤ ⎡ 2 x + 2 x C o s ( x ) − 3 S en ( x ) ⎤
5 2 2 2
⎡
⎢ 2x + C os ⎜ ⎟⎥ ⎢ ⎥
⎣ ⎝ x3 ⎠⎦ ⎣ ⎢ x4 ⎥
⎦
⎛x⎞ ⎛x⎞
tg ⎜ ⎟ + ctg ⎜ ⎟
55) y = ⎝2⎠ ⎝2⎠
x
⎡1 2 ⎛ x ⎞ 1⎛ 2 ⎛ x ⎞ ⎞⎤ ⎡ ⎛x⎞ ⎛ x ⎞⎤
⎢ 2 S ec ⎜ 2 ⎟ + 2 ⎜ − csc ⎜ 2 ⎟ ⎟ ⎥ x + ⎢ tg ⎜ 2 ⎟ + ctg ⎜ 2 ⎟ ⎥
⎝ ⎠ ⎝ ⎝ ⎠ ⎠⎦ ⎣ ⎝ ⎠ ⎝ ⎠⎦
y′ = ⎣ 2
x
x ⎡ 2 ⎛ x⎞ 2 ⎛ x ⎞⎤ ⎡ ⎛ x ⎞ ⎛ x ⎞⎤
2 ⎣⎢ S ec ⎜ 2 ⎟ − csc ⎜ 2 ⎟ ⎥ + ⎢ tg ⎜ 2 ⎟ + ctg ⎜ 2 ⎟ ⎥
⎝ ⎠ ⎝ ⎠⎦ ⎣ ⎝ ⎠ ⎝ ⎠⎦
y′ = 2
x
⎡ ⎤ ⎡ ⎛x⎞ ⎛ x ⎞⎤
x ⎢ 1 1 ⎥ ⎢ S en ⎜ 2 ⎟ C o s ⎜ 2 ⎟ ⎥
− ⎢ − ⎥+⎢ ⎝ ⎠+ ⎝ ⎠⎥
2 ⎢ 2 ⎛ x ⎞ 2 ⎛ x ⎞ ⎥ ⎢ C os ⎛x⎞ ⎛ x ⎞⎥
S en ⎜ ⎟ C o s ⎜ ⎟ ⎜ ⎟ S en ⎜ ⎟ ⎥
⎢
⎣ ⎝2⎠ ⎝ 2 ⎠⎥ ⎢⎦ ⎣ ⎝2⎠ ⎝ 2⎠⎦
y′ = 2
x

28


⎡ ⎛x⎞ 2 ⎛ x ⎞⎤ ⎡ ⎛x⎞ 2 ⎛ x ⎞⎤
Cos 2 ⎜ ⎟ − Sen ⎜ ⎟ ⎥ ⎢ Sen 2 ⎜ ⎟ + Cos ⎜ ⎟ ⎥
x ⎢ ⎝2⎠ ⎝ 2 ⎠⎥ + ⎢ ⎝2⎠ ⎝ 2 ⎠⎥
− ⎢
2 ⎢ 2 ⎛ x ⎞ 2 ⎛ x ⎞ ⎥ ⎢ Cos ⎛ x ⎞ Sen ⎛ x ⎞ ⎥
Sen ⎜ ⎟ Cos ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎥
⎢
⎣ ⎝2⎠ ⎝2⎠ ⎥ ⎢ ⎦ ⎣ ⎝2⎠ ⎝2⎠ ⎦
y′ = 2
x
Sen 2 u = 2 Sen u Cos u ; Cos 2 u = Cos 2 u − Sen 2 u ; Sen 2 u + Cos 2 u = 1
⎡ ⎛x⎞ ⎤ ⎡ ⎤ ⎛x⎞ ⎛x⎞ ⎛ x⎞
Cos 2 ⎜ ⎟ − x Cos 2 ⎜ ⎟ + 2 Cos ⎜ ⎟ Sen ⎜ ⎟
x⎢ ⎝2⎠
⎥ ⎢ 1 ⎥
⎝ 2⎠ ⎝ 2⎠ ⎝2⎠
− ⎢ ⎥ + ⎢ ⎥
2⎢ ⎛ x⎞ ⎛ x ⎞⎥ ⎢ Cos ⎛ x⎞ ⎛ x ⎞⎥ ⎛x⎞ ⎛x⎞
Sen 2 ⎜ ⎟ Cos 2 ⎜ ⎟ ⎜ ⎟ Sen ⎜ ⎟ ⎥ Sen 2 ⎜ ⎟ Cos 2 ⎜ ⎟
⎢
⎣ ⎝2⎠ ⎝ 2 ⎠⎦⎥ ⎢
⎣ ⎝2⎠ ⎝ 2 ⎠⎦ ⎝2⎠ ⎝2⎠
y′ = y′ =
x2 2x2
⎛x⎞ ⎛x⎞
− x Cos ( x ) + 2 Sen ⎜ ⎟ Cos ⎜ ⎟
y′ = ⎝ 2⎠ ⎝2⎠
⎡ 2 2 ⎛ x ⎞ 2 ⎛ x ⎞⎤
⎢ 2 x Sen ⎜ 2 ⎟ Cos ⎜ 2 ⎟ ⎥
⎣ ⎝ ⎠ ⎝ ⎠⎦
3Sen x − 2Cos x 3Sen x − 2Cos x 1
56) y = ⇒y = ⇒y= 3Sen x − 2Cos x
5 5 5
1 ⎡1 ⎤
⎢ 2 ( 3Sen x − 2Cos x ) ( 3Sen x − 2Cos x ) ′ ⎥
−1
y′ = 2

5 ⎣ ⎦
1 ⎡1 −1 ⎤
y′ = ⎢ 2 ( 3Sen x − 2Cos x ) 2 ( (3Sen x)′ − ( 2Cos x)′ ) ⎥
5 ⎣ ⎦
1 ⎡1 −1 ⎤ 3 Cos x + 2 Sen x
y′ = ⎢ 2 ( 3Sen x − 2Cos x ) 2 (3 Cos x + 2 Sen x) ⎥ ⇒ y′ =
5 ⎣ ⎦ 2 5 3Sen x − 2Cos x

57)f(x) = αSen 2 (βx) + βCos 2 (βx)
2 αSen( βx) Cos (βx) + 2 β 2 Cos (βx) ( − Sen (βx)) 2 Sen (βx) Cos (βx) [ α − β ]
f'(x) = ⇒ f'(x) =
2 αSen (βx) + βCos (βx)
2 2
2 αSen 2 (βx) + βCos 2 (βx)
2 (Sen (βx) Cos (βx)) β [ α − β ]
f'(x) = Pero:2 Cos (βx) Sen (βx) = Sen( 2 β x )
2 αSen 2 (βx) + βCos 2 (βx)
β(α − β) Sen (2 β x )
f'(x) =
2 αSen 2βx + β Cos 2 βx

Senx − Cosx
58).y =
Senx + Cosx
⎡ ⎛ Cosx
⎢⎜ +
Senx ⎞
⎟
⎝ 2 Senx 2 Cosx ⎠
( Senx + Cosx − ) ( Senx − ) ⎛ 2Cosx − 2 Senx ⎞ ⎤
Cosx ⎜
⎝ Senx
⎟⎥
Cosx ⎠
y' = ⎢ ⎥
⎢
( ) ⎥
2
⎢ Senx + Cosx ⎥
⎣ ⎦

29


(Cosx Cosx) + Senx( Senx) ( Senx + ) ( Senx − ) (Cosx2Cosx) − Senx()Senx)
2 ( Senx Cosx) ( Senx Cosx
Cosx − Cosx

y' =
2
( Senx + Cosx
)

2 2 2 2
Cosx Senx Cosx + (Cos x + Sen x) + Senx Senx Cosx − Senx Cosx
Cosx + (Sen x + Cos x) − Senx Senx Cosx
Y' =
2
(2 Senx Cosx Senx + Cosx
)( )

Cosx Senx Cosx + 1 + Senx Senx Cosx − Senx Cosx
Cosx + 1 − Senx Senx Cosx
Y´=
2
( Senx + Cosx (2 Senx Cosx
) )

2
y' =
2
( Senx + Cosx (2 Senx Cosx
) )

c. Funciones Trigonométricas Inversas.

1 d ( 2x − 3)
59)y = arcsen ( 2 x − 3) ⇒ y´ = .
1 − ( 2x − 3) dx
2

2 2 1
y´ = ⇒ y´ = ⇒ y´ =
1 − 4x + 12x − 9
2
−4x + 12x − 8
2
3x − x2 − 2

2x 2x
60)y = arccos(x2 ) ⇒ y´ =− ⇒ y´ =−
1 − (x2 )2 1 − x4
1 6x
61) y = arc tan(3x2 ) ⇒ y´ = 6x ⇒ y´ =
1 + ( 3x )
2 2 1 + 9x4

⎡1 + x ⎤
62)y = arccot ⎢
(1 − x ) 1 − (1 + x ) ( −1)
⎥ ⇒ y´ =−
⎣1 − x ⎦
2
⎛1 + x ⎞
⎟ (1 − x )
2
1+ ⎜
⎝1 − x ⎠
−(1 − x + 1 + x) − 2 (1 − 2x + x2 )
y´ = ⇒ y´ =
⎡ 1 + 2x + x2 ⎤ (1 − 2x + x2 + 1 + 2x + x2 ) (1 − x )
2

(1 − x )
2
1+
⎢ 1 − 2x + x2 ⎥
⎣ ⎦
− 2 (1 − x )
2
1
y´ = ⇒ y´ = −
2 (1 + x ) (1 − x ) 1 + x2
2 2

30


⎡1⎤
63) y = x arc csc ⎢ ⎥ + 1 − x 2
⎣x⎦
⎡1⎤
y ´ = arc csc ⎢ ⎥ + x
( −1) ⎛ − 1 ⎞ + −2 x
⎜ 2⎟
⎣x⎦ 1 1 2
−1 ⎝ x ⎠ 2 1 − x
x x 2
1 x x ⎡1⎤
y ´ = arc csc + − ⇒ y´= arc csc ⎢ ⎥
x ⎣x⎦
1 − x2 1 − x2
b
sec 2 x
1 ⎛b ⎞ 1 a
64)y = arc tan ⎜ tan x ⎟ ⇒ y´ = 2
ab ⎝a ⎠ ab ⎛b ⎞
1 + ⎜ tan x ⎟
⎝a ⎠
1 b Sec 2 x Sec 2 x 1
y´ = ⇒ y´ = 2 ⇒ y´ = 2 2
ab a (a + b an x)
2 2 2
a + b tan x
2 2
a cos x + b 2 sen 2 x
a2
x2 − 4 1 ⎡x ⎤ 1 ⎡x⎤
+ arc sec ⎢ ⎥ ⇒ y = x −2 ( x 2 − 4 ) + arc sec ⎢ ⎥
1/2
65) y = 2
x 2 ⎣2 ⎦ 2 ⎣2⎦
1/2 2x 1 1 1
y´ = − 2x −3 ( x 2 − 4 ) + x −2 ( x 2 − 4 )
1/2
+ 1/2
( )
2 2 x ⎛ x2 ⎞ 2
⎜ − 1⎟
2 ⎝ 4 ⎠
−2 ( x 2 − 4 )
1/2
1 1
y ´= + +
x (x2 − 4) x (x2 − 4)
3 1/2 1/2
x

−2 ( x 2 − 4 ) + x 2 + x 2 8
y´ = ⇒ y´ =
x3 ( x2 − 4)
1/2
x3 x2 − 4
x−a
66) y = ( x − a ) 2 a x − x 2 + a 2 arc sen
a

y´ = 2ax − x 2 +
( x − a )( 2a − 2x ) +
a2 1
2 2ax − x (x − a) a
2 2

1−
a2

y´ = 2ax − x 2 +
( x − a ) (a − x ) +
a2
2ax − x 2 2ax − x 2

y´=
2ax − x 2 + xa − a 2 − x 2 + ax + a 2
⇒ y´ =
( 2ax − x ) 2 ⇒ y´ =
2

2ax − x 2
2ax − x 2
2ax − x 2

31


1 − tg x
67)y = arc tg
1 + tg x
⎡ ⎤
⎢ ⎡ − Sec2 x (1 + tg x) − (1 − tg x) Sec2 x ⎤ ⎥
1 ⎢ 1
y′ = ⎢ ⎥⎥
⎡1 − tg x ⎤ ⎢ 1 − tg x ⎢ (1 + tg x )
2
⎥⎥
1+ ⎢ ⎥ ⎢ 2 1 + tg x ⎣
1 + tg x ⎦ ⎣
⎦⎥
⎣ ⎦
⎡ ⎤ ⎡ ⎤

y′ =
1
⎢
⎢ 1 ⎡ − Sec2 x (1 + tg x + 1 − tg x ⎤
⎢ ⎥
⎥ ⎢
⎥ ⇒ y′ = (1 + tg x) ⎢ 1 ( − Sec x ) ⎥
2
⎥
1 + tg x + 1 − tg x ⎢ 1 − tg x ⎢ (1 + tg x )
2
⎥ ⎥ 2 ⎢ 1 − tg x (1 + tg x )2 ⎥
⎢2 ⎣ ⎦⎥ ⎢2 ⎥
1 + tg x 1 + tg x
⎣ ⎦ ⎣ 1 + tg x ⎦
− Sec x
2
− Sec x
2
− Sec x
2
− Sec x
2
y′ = ⇒ y′ = ⇒ y′ = ⇒ y′ =
1 − tg x 1 − tg x 2 (1 − tg x )(1 + tg x ) 2 1 − tg 2 x
(1 + tg x ) (1 + tg x )
2 2
2 2
1 + tg x 1 + tg x
1 b
68) y = arcsen x
b a
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎡ b ⎤
1 ⎢ 1 ⎥⎛ b⎞ 1 ⎢ 1 b⎥ 1 ⎢⎢ ⎥
y′ = a ⎥
⎢ 2⎥ ⎜
⎜ ⎟ ⇒ y′ =
⎟ ⎢ ⎥ ⇒ y′ =
b ⎢a + x b⎥
2 2
b ⎢ ⎡ b⎤ ⎥ ⎝ a ⎠ b ⎢ ⎡ b⎤ a⎥
⎢1 + ⎢x ⎥ ⎥ ⎢1 + ⎢ x a ⎥ ⎥ ⎢
⎣ a ⎥
⎦
⎣ ⎣ a⎦ ⎦ ⎣ ⎣ ⎦ ⎦
1 ⎡ a b ⎤ a a
y′ = ⎢ ⎥ ⇒ y′ = ⇒ y′ =
⎢ a (a + x b) ⎥ a (a + x 2 b) a + x2 b
2
b ⎣ ⎦
⎡x⎤
69)f(x) = x a 2 − x 2 + a 2arcsen ⎢ ⎥ ⇒ f´(x) = a 2 − x 2 + x
( −2x ) + a 2 1 ⎡1⎤
⎣a ⎦ ⎢a ⎥
2 a2 − x2 x ⎣ ⎦
2
1− 2
a
x2 a a2 − x2 − x2 + a2
f ´(x) = a 2 − x 2 − + ⇒ f´(x) = ⇒ f ´ (x) = 2 a 2 − x 2
a −x
2 2
a −x
2 2
a −x
2 2

a2
x
70) y = 3a 2 arc tg − ( 3a + 2x ) a x − x 2
a−x

3a 2 ⎡1 ⎛ x ⎞ −1
2 ⎛ ( a − x ) − x ( −1) ⎞ ⎤ ⎡ 1 ⎤
⎟ ⎥ − ⎢2 ax − x 2 + ( 3a + 2x ) ( ax − x 2 ) 2 ( a − 2x ) ⎥
−1
y′ = ⎢ ⎜ ⎟ ⎜
⎛ x ⎞ ⎢2 ⎝ a −x ⎠ ⎜ ( a − x ) ⎠⎦
2
⎟⎥ ⎣ 2 ⎦
1− ⎜ ⎟ ⎣ ⎝
⎝ a−x ⎠

32


⎡ ⎤
⎢ ⎥
3a ⎢2
a −x +x ⎥ − ⎡2 ax − x2 + ( 3a + 2x) 1 ( ax − x2 ) 2 ( a − 2x) ⎤
−1
y′ = ⎢ ⎥
a −x−x ⎢ 2⎥
( a − x) ⎥ ⎣
x 2 ⎦
⎢ 2
( a − x) ⎣ a − x ⎦
⎡ ⎤
2 ⎢ ⎥
3a ⎢ a
(
⎥ − ⎡( ax − x2 ) 2 2( ax − x2 ) + ( 3a + 2x)( a − 2x) ⎤)
−1
y′ = ⎢ ⎥
a − 2x ⎢ x 2⎥ ⎣ ⎦
⎢2 ( a − x) ⎥
⎣ a −x ⎦
3a3
− ⎡( ax − x2 ) ( 2ax − 2x + 3a2 − 6ax + 2ax − 4x2 ) ⎤
−1
y′ = 2 2

2(a − 2x) x ( a − x) ⎢⎣ ⎥
⎦

⎡ 3a3 ⎤ ⎡3a2 − 6x2 − 2ax ⎤ ⎡ 3a3 ⎤ ⎡3a2 − 6x2 − 2ax ⎤
y′ = ⎢ ⎥−⎢ ⎥ ⇒ y′ = ⎢ ⎥−⎢ ⎥
⎢ 2( a − 2x) ax − x2 ⎥ ⎢ ( ax − x2 ) 2 ⎥ ⎢ 2( a − 2x) ax − x2 ⎥ ⎣
1
⎣ ⎦ ⎢ ⎣ ⎦ ⎢ ax − x2 ⎥ ⎦
⎣ ⎥
⎦
Sen x − 1
71) y = arc ctg
Senx + 1

−1 ⎡ 1 ⎛ Senx − 1⎞−12 ⎛ Cosx ( Sen x + 1) − ( Senx − 1) Cosx ⎞⎤
y′ = ⎢ ⎜ ⎟ ⎜ ⎟⎥
⎛ Senx − 1⎞ ⎢ 2 ⎝ Senx + 1⎠ ⎜ (Senx + 1)
2
⎟
1+ ⎜ ⎟ ⎣ ⎝ ⎠⎥
⎦
⎝ Senx + 1⎠
⎡ ⎤
⎢ ⎥
−1 ⎢ 1 ⎛ Cosx ( Sen x + 1 − Senx + 1) ⎞⎥
y′ = ⎜ ⎟⎥
Senx + 1 + Senx − 1 ⎢ ⎛ 1
⎜ (Senx + 1)
2
⎟
⎢ 2 Senx − 1⎞
2
⎝ ⎠⎥
Sen x + 1 ⎜
⎢ Sen x + 1 ⎟ ⎥
⎣ ⎝ ⎠ ⎦
⎡ ⎤
⎢ ⎥
y′ =
−1 ⎢ 1 ( 2Cosx) ⎥
2Sen x ⎢ ⎛ 2⎥
⎢ 2 Sen x − 1⎞ ( Senx + 1) ⎥
1
2

Senx + 1 ⎢ ⎜ ⎟ ⎥
⎣ ⎝ Senx + 1⎠ ⎦
− Cosx − Cosx
y′ = ⇒ y′ =
Sen x − 1 (Sen x − 1) (Senx + 1)
2
2Sen x (Sen x + 1) 2 Senx
Senx + 1 (Senx + 1)
− Cosx − Cosx − ctgx
y′ = ⇒ y′ = ⇒ y′ =
2 Sen x (Sen x − 1) (Senx + 1) 2 Senx Sen2 x − 1 2 Sen2 x − 1

33


⎛ 1+ x ⎞ ⎡ (1 − x) − (1 + x)( − 1) ⎤
1
72) y = Arctg ⎜ ⎟ ⇒ y' = ⎢ ⎥
⎝ 1− x ⎠ (1 − x)2
2
⎛ 1+ x ⎞ ⎣ ⎦
1+ ⎜ ⎟
⎝ 1− x ⎠
(1 − x) + (1 + x) ⎡1 − x + 1 + x ⎤
2 2
2 2
y' = ⎢ (1 − x)2 ⎥ ⇒ y' = (1 + x)2 + (1 + x)2 ⇒ y' = 1 − 2x + x 2 + 1 + 2x + x 2
(1 − x) 2
⎣ ⎦
2 2 1
y' = → y' = ⇒ y' =
2 + 2x 2
2(1 + x )
2
1+ x2

1 1 ⎡ 2( Arcsenx) ( Arcsenx)2 (−1) ⎤
73) y = ( Arcsenx)2 Arc cos x) ⇒ y ' = ⎢ Arc cos x + ⎥
2 2 ⎣ 1 − x2 1 − x2 ⎦
Arcsenx Arcsenx(2 Arc cos x − Arcsenx )
y' = [ 2 Arc cos x − Arcsenx ] ⇒ y ' =
2 1− x 2
2 1 − x2
′
⎛ x ⎞
⎜ ⎟
⎛ x ⎞ ⎝ 1+ x ⎠
2
74)y = Arcsen ⎜ ⎟ ⇒ y' =
⎝ 1+ x ⎠
2 2
⎛ x ⎞
1− ⎜ ⎟
⎝ 1+ x ⎠
2

⎡1 ⎤
1 + x 2 − x ⎢ (1 + x 2 )−1/2 (2x) ⎥
⎣2 ⎦ (1 + x 2 )1/2 − x 2 (1 + x 2 )−1/2
(1 + x )
2
(1 + x 2 )
y' = ⇒ y' =
x2 1+ x2 − x2
1−
1+ x2 1+ x2
(1 + x 2 )−1/2 ⎡1 + x 2 − x 2 ⎤
⎣ ⎦ 1
(1 + x )2
(1 + x 2 ) 3 1+ x2 1+ x2 1
y' = ⇒ y' = ⇒ y' = ⇒ y' = ⇒ y' =
1 1 (1 + x 2 ) 3 (1 + x )
2 3
1+ x2
1+ x2 1+ x2

⎡ xsenx ⎤
75)y = Arctg ⎢
⎣1 − xcosx ⎥⎦
1 ⎡ (Senx + x(Cosx))(1 − xcosx) + (xsenx)(Cosx + x( − Senx) ⎤
y' = ⎢ ⎥
2
x Sen x2
(1 − xcosx)2
+1 ⎣ ⎦
(1 − xCosx)2
(Senx + xcosx)(1 − xcosx) + (xsenx)(Cosx − xSenx)
y' =
⎛ (1 − xcosx)2 + (xsenx)2 ⎞
⎟ (1 − xcosx)
2
⎜
⎝ (1 − xcosx)2 ⎠
34


Senx − xsenx Cosx + xcosx − x 2Cos2 x + xsenx Cosx − x 2Sen 2 x
y' =
1 − 2xcosx + x 2Cos2 x + x 2Sen 2 x
Senx + xcosx − x 2Cos2 x − x 2Sen 2 x
y' =
1 − 2xcosx + x 2 (Cos2 x + Sen 2 x)
Senx + xcosx − x 2 (Cos2 x + Sen 2 x) Senx + xcosx − x 2
y' = ⇒ y' =
(1 − 2xcosx + x2 ) (1 − 2xcosx + x 2 )
1 ′
⇒ y = ( Arctgx ) ⇒ y' =−1( Arctgx ) ( Arctgx )
−1 −2
76)y =
Arctgx
−1 ⎛ 1 ⎞ −1
y' = 2 ⎜ 2 ⎟
⇒ y' =
(Arctgx) ⎝ 1 + x ⎠ (1+ x ) (Arctgx)2
2

1 ′
( Arctgx ) − (Arcsenx)3 ⇒ y' = ( Arctgx ) ( Arctgx )
−1/2
77)y = − 3(Arcsenx)2 (Arcsenx)′
2
1 ⎛ 1 ⎞ ⎛ 1 ⎞ 1 −3(Arcsenx)2
y' = ⎜ 2 ⎟
− 3(Arcsenx)2 ⎜ ⎟ ⇒ y' =
2 Arctgx ⎝ 1 + x ⎠ ⎝ 1+ x
2
⎠ 2 (1 + x 2 ) Arctgx 1 + x2

1 − Cosx
78)y = ArcTg
1 + Cosx
−1/2
1 ⎛ 1 − Cosx ⎞
⎜ ⎟
2 1 + Cosx ⎠ ⎡ Senx(1 + Cosx) − (1 − Cosx)( − Senx) ⎤
y' = ⎝ ⎢ ⎥
⎛ 1 − Cosx ⎞ ⎣ (1 + Cosx)2 ⎦
1+ ⎜ ⎟
⎝ 1 + Cosx ⎠

y' =
[Senx(1+ Cosx +1− Cosx)]
⎛ ⎛ 1 − Cosx ⎞ ⎞ 1 − Cosx
⎜1 + ⎜ 1 + Cosx ⎟ ⎟ 2 1 + Cosx (1 + Cosx)
2

⎝ ⎝ ⎠⎠

y' =
[ 2Senx] ⇒ y' =
(1 + Cosx)Senx
⎛ 1 + Cosx + 1 − Cosx ⎞ 1 − Cosx 1 − Cosx
⎜ ⎟2 (1 + Cosx)2 2 (1 + Cosx)2
⎝ 1 + Cosx ⎠ 1 + Cosx 1 + Cosx
Senx Senx
y' = ⇒ y' = ⇒
1 − Cosx 2 (1 − Cosx)(1 + Cosx)
2 (1 + Cosx) 2

1 + Cosx
Senx Senx 1
y' = ⇒ y' = ⇒ y' =
2 1 − Cos x 2 2Senx 2

35


d. Funciones Logarítmicas y Exponenciales.

( ) ( )
1 d ⎛ 6x log e ⎞
79)y = log 3x 2 − 5 ⇒ y ´ = log e 3x 2 − 5 ⇒ y´ = ⎜ a ⎟
a
3x 2 − 5
a dx ⎜ 3x 2 − 5 ⎟
⎝ ⎠

2 ( x + 3) 2
80)y = Ln ( x + 3)2 ⇒ y´ = ⇒ y´ =
( x + 3)2 x+3

1 2 Ln ( x + 3)
81)y = Ln 2 ( x + 3) ⇒ y´ = 2 Ln ( x + 3) ⇒ y´ =
x+3 x+3

sec x + tanx + sec2 x
82)y = Ln ( sec x + tanx ) ⇒ y´ = ⇒ y´ = sec x
sec x + tanx

83)y = x ( sen (ln x) − cos(ln x) )

⎛ cos(ln x) sen (ln x) ⎞
y´ = ( sen (ln x) − cos(ln x) ) + x ⎜ + ⎟ ⇒ y´ = 2sen (ln x)
⎝ x x ⎠

3 3
84)y = ex ⇒ y´ = ex 3x 2

sen (3x) sen (3x)
85)y = e ⇒ y´ = 3cos(3x)e

86) y = x 2 ex ⇒ y´ = 2x ex + x 2ex ⇒ y´ = ex ( x 2 + 2x )

87)y = e−x cos (x) ⇒ y´ = − e−x cos (x) + e−x ( − sen ( x) ) ⇒ y´ = e−x ( sen (x) + cos( x) )

36


88)y = x 2 e 2x cos (3x)

y´ = 2x e2x cos (3x) + x 2 (2 e2x )cos(3x) + x 2 e 2x ( −3sen (3x) )

y´ = x e2x ( 2 cos (3x) + 2x cos (3x) − 3x sen (3x) )

( )⎤ ⎡ ( 3x 2 ) ⎤ (1 − x3 ) (1 − x3 )
89).y = ⎡ Ln ( x 3 + 2 ) ⎤ ⎡e + Ln ( x 3 + 2 ) e ( −3x 2 )
1 − x3
⇒ y´ = ⎢ 3 ⎥e
⎣ ⎦⎢⎣ ⎥
⎦ ⎢ ( x + 2) ⎥
⎣ ⎦

(1 − x3 ) ⎡1 − ( x + 2 ) Ln ( x + 2 ) ⎤
3 3
(1 − x ) ⎡ 1 ⎤
− Ln ( x 3 + 2 ) ⎥ ⇒ y´ = 3x 2 e
3

y´ = 3x 2 e ⎢ x3 + 2 ⎢ ⎥
⎣ ⎦ ⎢
⎣ ( x3 + 2) ⎥
⎦

(1 − x ) 1 − x 3 + 2 Ln x 3 + 2
( ( ) ( ) )
3

3x 2 e
y´ =
(x 3
+ 2)

'
x2 − 1 x2 − 1 ⎛ 2 ⎞
90)y = 4e ⇒ y′ = 4e Ln 4 ⎜ e x − 1 ⎟
⎜ ⎟
⎝ ⎠
x −1
2 ⎡ 1 −1 ⎤
Ln 4 ⎢e x − 1 ( x 2 − 1) 2 (2x) ⎥
2
y′ = 4e
⎢
⎣ 2 ⎥
⎦

⎛ x2 − 1 ⎞
Ln 4 ⎟ x e x − 1
2
⎜ 4e
⎜ ⎟
x2 − 1 ⎡ −1 ⎤
Ln 4 ⎢ x e x − 1 ( x 2 − 1) 2 ⎥ ⇒ y′ = ⎝ ⎠
2
y′ = 4e
⎢
⎣ ⎥
⎦ x2 − 1

e 2x − 1
e x − e− x e2x − 1ex
91)F(x) = ⇒ F(x) = 2x ⇒ F(x) = 2x
e x + e− x e +1 e +1
e x

2 e 2x ( e2x + 1) − ( e2x − 1)( 2 e 2x ) 2 e 2x ⎡ e 2x + 1 − e2x + 1⎤
⎣ ⎦ 4e 2x
F´(x) = ⇒ F´(x) = ⇒ F´(x) =
(e + 1) (e + 1) (e + 1)
2x 2 2x 2 2x 2

37


e− x
92) y = x ⇒ y´=
−e −x
( e + 1) − e ( e )
x −x x

e +1 ( e + 1)
x 2

−e − x ⎡ e x + 1 + e x ⎤
⎣ ⎦ ⇒ y´= − e ⎡ 2e + 1⎤
−x
⎣
x
⎦
y´ =
( e + 1) ( e + 1)
x 2 x 2

1+
1
(1 + x 2 )−1/2 ( 2x )
(
93)y = Ln x + 1 + x 2
) ⇒ y´ = 2
x + 1+ x 2

1 +
x (1 + x )1/2 + x
2

y´ =
(1 + x )1/2 ⇒ y´ = 2
(1 + x )1/2 2

1/2 1/2
x + (1 + x ) 2
x + (1 + x ) 2

⎡ 2 1/2 ⎤
⎢ (1 + x )
⎣
+ x⎥
⎦ 1
y´ = ⇒ y´ =
⎡ 1/2 ⎤
⎢ x + (1 + x ) ⎦ (1 + x )
2
⎥
2 1/2
(1 + x )2

⎣

1
⎛
1 − x2 1 − x2 ⎞
2
⎜ ⎟
⎜ ⎟
x2 + 1 x + 1⎟
2
94)F(x) = e
⎜
⇒ y =e
⎜ ⎟
⎝ ⎠

1
⎛
1 − x2 ⎞
2 −1
⎛ 2 ⎞
⎜1 − x ⎟
2
⎜ ⎟
⎛ ⎞
⎜ ( − 2x) ( x + 1) − (1 − x 2x ) ⎟
⎜ ⎟ 2 2
⎜
x + 1⎠ 1 ⎜ x + 1⎟
2 ⎟ ⎜
y´ = e ⎜
⎝
⎟
⎜
⎝
2 ⎟
⎟
⎠
⎜ ⎟
2 ⎜
⎝ ( x 2 + 1)2 ⎟
⎠
1 − x2 1 − x2
( ) ⎥ ⇒ y´ = 1 e x + 1
x 2 + 1 ⎡ −2x x 2 + 1 + 1 − x 2 ⎤ 2
⎡ ⎤
1e ⎢ ⎢ −2 x (2) ⎥
y´ =
1 − x2 ⎢ ( x 2 + 1) ⎥ ⎢ ( x 2 + 1)2 ⎥
2
2 2 1 − x2
⎣ ⎦ ⎣ ⎦
x2 + 1 x2 + 1
1 − x2 1 − x2
x2 + 1 x2 + 1
−2 x e −2 x e
y´ = ⇒ y´ =
(1 − x ) ( x
2
2
+ 1) (1 − x ) ( x 2 2
+ 1)
3
( x + 1)
2

38


( )
2
( x + 4 + x2 )′
( ) ⇒y=
2
95)y = Ln x + 4 + x2
(x + 4+ x )
2
2

y' =
(
2 x + 4 + x2 (1+ ) 1
2
( 4 + x2 ) ( 2x) )
−1/2
2 ⎡1+ ( 4 + x2 ) ⎤
⇒ y' = ⎣
⎢
−1/2

⎥
⎦
( x + 4 + x2
2

) x + 4+ x 2
( )
2 ⎢( 4 + x2 ) + x⎤
⎡ 1/2
⎡ ⎤ ⎡ ( 4 + x2 )1/2 + x ⎤
2⎢1+ x ⎥ ⇒ y' = 2 ⎢ ⎥ ⇒ y' = ⎣ ⎥
⎦ 2
y' = ⇒ y' =
x + 4 + x2 ⎢ ( 4 + x2 ) ⎥ ⎢ ( 4 + x2 ) ⎥ ⎡( 4 + x2 )1/2 + x⎤ ( 4 + x2 )1/2
1/2 1/2
x + 4 + x2 4 − x2
⎣ ⎦ ⎣ ⎦ ⎢
⎣ ⎥
⎦
2Lnx 1 2Ln x − x
2
96)y = Ln2x − Ln(Lnx) ⇒ y' = − ⇒ y' =
x xLnx xLnx
(α x)
(αsen(βx) −βCos(βx)) e
97)f(x) =
α 2 + β2
⎡ ⎤
⎡−α βCos(βx) − β2Sen(βx)⎤ eα x + ⎢α 2eα xSen(βx) −αβeα xCos(βx)⎥
⎣ ⎦
f'(x) = ⎣ ⎦
α +β
2 2

α x ⎡2α βCos(βx) + Sen(βx)(β2 −α 2 )⎤
−eα x (α βCos(βx) + β2Sen(βx) −α 2Sen(βx) + α βCos(βx)) −e ⎣ ⎦
f'(x) = ⇒ f'(x) =
α 2 + β2 α +β
2 2

⎡1+ Cosx ⎤
98)y = Ln ⎢ ⎥ + 2ArcTg ( Cosx )
⎣1− Cosx ⎦
1 −1/2 1 −1/2
( Cosx) ( − Senx) ⎡1 − Cosx ⎤ − (1 + Cosx) ( Cosx)
⎣ ⎦ ( − Senx)1 2( 1( Cosx)−1/2 (−Senx))
y' = 2 2 + 2
(
1+ Cosx
1− Cosx ⎣ )
⎡1 − Cosx ⎤
⎦
2 1+Cosx

y' =
−Senx
2 Cosx
[
1− Cosx −(1+ Cosx)
Senx
]
2 Cosx
+
Senx ( )
(1+ Cosx)(1− Cosx) (1+Cosx) Cosx
−Senx
2 Cosx
(
1− Cosx +1+ Cosx
Senx
)
y' = +
(1+ Cosx)(1− Cosx) (1+Cosx) Cosx

39


−2Senx −Senx
2 Cosx Senx Cosx Senx
y' = + ⇒ y' = −
(1 + Cosx)(1 − Cosx) (1+Cosx) Cosx (1+ Cosx)(1− Cosx) (1+Cosx) Cosx
Senx
Cosx − Senx Senx Senx
y' = ⇒ y' = −
(1−Cosx) (1+Cosx) Cosx (1−Cosx) Cosx (1+Cosx) Cosx
Senx(1+Cosx)−Senx(1−Cosx) Senx(1+Cosx−1+Cosx)
y' = ⇒ y' =
(1−Cosx)(1+Cosx) Cosx (1−Cos2x) Cosx
Senx(2Cosx) (2Cosx) 2Ctgx
y' = 2
⇒ y' = ⇒ y' =
Sen x Cosx Senx Cosx Cosx

2 tg x − 2 tg x + 1
99)y =
4
ln
tg x + 2 tg x + 1
+
2
2
arctg ( 2 tg x −1 + ) 2
2
arctg ( )
2 tg x + 1

⎛ ⎛ 2 Sec2 x ⎞ ⎛ 2 Sec2 x ⎞ ⎞
⎜ ⎜ Sec x −
⎜
⎛ 2 ⎞ ⎜ tg x +1 + 2tg x ⎝ ⎟
2tg x ⎠
(
⎟ tgx +1+ 2tg x − ⎜ Sec x +
⎜ ⎟
2tg x ⎠
)
⎟ tgx +1− 2tg x ( )⎟
⎟
y´ = ⎜ ⎟ ⎜ ⎝
⎜ 4 ⎟ tg x + 1− 2tg x ⎟
( )
2
⎝ ⎠⎜ tgx + 1 + 2tg x ⎟
⎜ ⎟
⎝ ⎠
⎛ ⎞ ⎛ ⎞
⎜ 2 Sec2 x ⎟ ⎜ 2 Sec2 x ⎟
+⎜ . + .
( ) 2tg x ⎟ ⎜ 1 + 2tg x − 1( 2tg x ⎟ )
2 2
⎜ 1 + 2tg x − 1 ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
2
Sec x
Factor común:
2tg x

( )( ) (
⎛ 2 Sec2 x ⎞ ⎛ 2tg x −1 tg x +1+ 2tg x − 2tg x + 1 tg x +1− 2tgx ⎞
y´ = ⎜ ⎜ ⎟
)( )
⎜ 4 2tg x ⎟ ⎜
⎝
⎟
⎠⎝ ( )(
tg x +1− 2tg x tg x +1+ 2tg x ⎟
⎠ )
⎛ 2 ( tg x + 1) ⎞
+⎜ ⎟
( )(
⎜ tg x +1− 2tg x tg x +1+ 2tg x ⎟
⎝ ⎠ )
Sec2 x 4tg x
y´ = . = tg x
2tg x ( tg x + 1) − 2tg2 x
2

2
⎛ 1 ⎞ 1
2x ⎜x + ⎟ +2
+ ln ⎝
2⎠
100)y = 2 arctg
1 − x2 ⎛ 1 ⎞
2
1
⎜x − ⎟ +2
⎝ 2⎠
⎡ ⎤⎡ ⎡ 2
⎤ ⎡ 2
⎤⎤
1 ⎥ ⎢ 2 ⎛ x + 1 ⎞ ⎢⎛ x + 1 ⎞ + 1 ⎥ − 2 ⎛ x + 1 ⎞ ⎢⎛ x + 1 ⎞ + 1 ⎥ ⎥
2
⎢ ⎛ 1 ⎞
x− + ⎜ ⎟ ⎜ ⎟ 2 ⎜ ⎟ ⎜ ⎟
⎢ 2 2 (1 − x + 2x ) ⎜ ⎟ 2⎥⎢ ⎝ 2⎦ ⎥
2 2
⎝ 2⎠ 2 ⎠ ⎣⎝
⎢ 2⎠ ⎥
⎦ ⎝ 2 ⎠ ⎣⎝
⎢ 2⎠ ⎥
y´= ⎢ 2
+ 2 ⎥⎢ 2 ⎥
⎢ ⎛ 2x ⎞ ⎛ 1 ⎞ 1 ⎥⎢ ⎡⎛ 1 ⎞
2
1⎤ ⎥
⎢1 + ⎜ 1 − x2 ⎟ (1 − x ) ⎜
2 2 x+ ⎟ +2 ⎥⎢ ⎢⎜ x + ⎟ + 2⎥ ⎥
⎝ 2⎠
⎣ ⎝ ⎠ ⎦⎢⎣ ⎣⎝
⎢ 2⎠ ⎥
⎦ ⎥
⎦
40


2 2 (1− x2 )
2

y´ = + (*)
⎡(1 − x2 )2 + 2x2 ⎤ (1 − x2 ) 2
⎢
⎣ ⎥
⎦
⎡⎛ 1 ⎞⎛ 1 ⎞
2
1⎛ 1 ⎞ ⎛ 1 ⎞⎛ 1 ⎞
2
1⎛ 1 ⎞⎤
2 ⎢⎜ x + ⎟⎜ x + ⎟ + 2⎜x + ⎟ − ⎜x − ⎟⎜ x + ⎟ − 2⎜x + ⎟⎥
⎢⎝ 2 ⎠⎝ 2⎠ ⎝ 2⎠ ⎝ 2 ⎠⎝ 2⎠ ⎝ 2⎠⎥
(*) ⎣ ⎦
⎡⎛ 1 ⎞
2
1 ⎤ ⎡⎛ 1 ⎞
2
1 ⎤
⎢⎜ x + ⎟ + 2 ⎥ ⎢⎜ x − ⎟ + 2⎥
⎢⎝
⎣ 2⎠ ⎥ ⎢⎝
⎦⎣ 2⎠ ⎥
⎦

⎧⎛ 1 ⎞⎛ 1 ⎞ ⎡⎛ 1 ⎞ ⎛ 1 ⎞⎤ 1 ⎡⎛ 1 ⎞ ⎛ 1 ⎞⎤ ⎫
2 2 (1− x )
2 ⎨⎜ x +
2 ⎟⎜ x − ⎟ ⎢⎜ x − ⎟ −⎜ x + ⎟⎥ + 2 ⎢⎜ x + ⎟− ⎜ x− ⎟⎥ ⎬
⎩⎝ 2 ⎠⎝ 2 ⎠ ⎣⎝ 2⎠ ⎝ 2 ⎠⎦ ⎣⎝ 2⎠ ⎝ 2 ⎠⎦ ⎭
y´ = +
1 + x4 ⎡( x2 + 1) + 2 x ⎤ ⎡( x2 +1) − 2 x ⎤
⎣ ⎦⎣ ⎦

⎡ 2 ⎤⎛ 1 ⎞⎛ 1 ⎞ 1 2 ⎡ ⎛ 2 1 ⎞ ⎤
2 2 (1− x )
2 ⎢− ⎥ ⎜ x +
2 ⎟⎜ x + ⎟+ 2 2 (1− x )
2 ⎢−2 ⎜ x − ⎟ + 1⎥
⎣ 2 ⎦⎝ 2 ⎠⎝ 2⎠ 2 2 ⎣ ⎝ 2⎠ ⎦
y´ = + ⇒ y´= +
1 + x4 ( x2 + 1) − 2 x2 1 + x4 1+ x4
2

2 2 (1 + x2 ) 2 ( −2 x2 + 2)
y´= +
1 + x4 1 + x4
2 2 (1 + x2 ) + 2 2 (1 − x2 ) 2 2 ⎡(1 + x2 ) + 2 2 (1 − x2 ) ⎤
⎣ ⎦= 4 2
y´ = =
1 + x4 1+ x 4
1 + x4

1 5 1
( x + 2) + LN ( 2x2 − 4x + 3) − 2 arctg ⎡ 2 ( x −1) ⎤
2
101)y = ⎣ ⎦
2 4 2
5 ( 4x − 4) 2⎡ 2 ⎤
y' = ( x + 2) + − ⎢ 2⎥
4 ( 2x 2 − 4x + 3) 2 ⎢1 + 2 ( x −1) ⎥
⎣ ⎦
20 ( x −1) 1 5 ( x −1) 1
y' = ( x + 2) + − ⇒ y' = ( x + 2) + − 2
4 ( 2x − 4x + 3) 1 + 2x − 4x + 2 ( 2x − 4x + 3) 2x − 4x + 3
2 2 2

( x + 2) ( 2x2 − 4x + 3) + 5x − 5 −1 2x3 − 4x 2 + 3x + 4x 2 − 8x + 6 + 5x − 5 − 1 2x3
y' = ⇒ y' = ⇒y= 2
( 2x 2
− 4x + 3) 2x 2 − 4x + 3 2x − 4x + 3

41


⎛ π⎞ ⎛ π⎞ ⎛ π ⎞⎛ 1 ⎞
102)y = Xsen ⎜ Lnx − ⎟ ⇒ y' = Sen ⎜ Lnx − ⎟ + Xcos ⎜ Lnx − ⎟ ⎜ ⎟
⎝ 4⎠ ⎝ 4⎠ ⎝ 4 ⎠⎝ x ⎠
⎛ π⎞ ⎛ π⎞
y' = Sen ⎜ Lnx − ⎟ + Cos ⎜ Lnx − ⎟ ⇒ Sen(A ± B) = SenA.CosB ± CosA.SenB;
⎝ 4⎠ ⎝ 4⎠
Cos(A ± B) = CosA.CosB ∓ SenA.SenB
⎛π⎞ ⎛π⎞ ⎛π⎞ ⎛π⎞
y' = Sen (Lnx) Cos ⎜ ⎟ − Cos(Lnx)Sen ⎜ ⎟ + Cos(Lnx) Cos ⎜ ⎟ + Sen ⎜ ⎟ Sen (Lnx)
⎝4⎠ ⎝4⎠ ⎝4⎠ ⎝4⎠
2 2 2 2
y' = Sen(Lnx) − Cos(Lnx) + Cos(Lnx) + Sen(Lnx) ⇒ y' = 2 Sen(Lnx)
2 2 2 2

e. Derivadas Implícitas.
−2x x
103)x 2 + y2 = 1 ⇒ 2x + 2yy´ = 0 ⇒ y´ = ⇒ y´ =−
2y y
y y [ y + xy´]
104)ex + e + Ln (x y) = 2 ⇒ ex + yé − =0
xy
y
xyex + xyyé − ( y + xy´) y
= 0 ⇒ xyex + xyyé − ( y + xy´) = 0
x.y

xyex − y + y´ ⎡xye − x ⎤ = 0 ⇒ ⎡ xye − x ⎤ = − xyex + y ⇒ y´ =
y y (
− xyex − y
⇒ y´ =
)
y − xyex
⇒ y´ =
y(1 − xex )
⎢
⎣ ⎥
⎦ ⎢
⎣ ⎥
⎦ y y y
x ye − x xye − x x(ye − 1)
105)x 2 + y2 + 2x − 4y − 6 = 0 ⇒ 2x + 2yy´ + 2 − 4y´ = 0

2x + 2 + y´ ( 2y − 4) = 0 ⇒ y´ = −
( 2x + 2) ⇒ y´ =
− ( x + 1)
2y − 4 ( y − 2)
y 1 y y 1
106)ex + Lny = e Ln x ⇒ ex + y´ = y´ e Lnx + e
y x
y y y
y´ y e xyex + xy´ − xyyé Lnx − ye
ex + − yé Lnx − = 0⇒ =0
y x xy
y y y y y
xyex + xy´ − xyyé Lnx − ye = 0 ⇒ xy´ − xyyé Lnx − ye =− xyex + ye
x y
y´ ⎡ x − xyey Ln x ⎤ =− xyex + yey ⇒ y´ = y(-xe + e )
⎢
⎣ ⎥
⎦ y
x(1− ye Ln x)

42


1 1
107). + xy + = 0 ⇒ x − 1 + xy + y − 1 = 0 ⇒ −x − 2 + y + xy′ − y − 2 y′ = 0
x y
−1 y′ − y2 + x2 y3 + x3y2y1 − x2y1
+ y + xy′ − = 0⇒ = 0
x2 y 2 x2y2

− y2 + x2y3 + x3 y2 y′ − x2 y′ = 0 ⇒ x3 y2 y′ − x2 y′ = y2 − x2y3

2 2 3 y2 ⎛1 − x2y ⎞
⎜ ⎟
y´ ⎡x3 y2 − x2 ⎤ = y2 − x2 y3 ⇒ y´ = y − x y ⇒ y´ = ⎝ ⎠
⎢
⎣ ⎥
⎦ ⎡x3 y2 − x2 ⎤ x2 ⎡xy2 − 1⎤
⎢
⎣ ⎥
⎦ ⎢
⎣ ⎥
⎦
108).xy + x − 2y − 1 = 0 ⇒ y + xy´ + 1 − 2y´ = 0
xy´ − 2y´ + y + 1 = 0 ⇒ y´ (x − 2) = − (y + 1)
− (y + 1) − (y + 1)
y´ = ⇒ y´ =
(x − 2) (2 − x )
109). x2y − xy2 − x2 + y2 = 0 ⇒ 2xy + x2y´ − ⎛ y2 + 2x yy´⎞ − 2x + 2yy´ = 0
⎜ ⎟
⎝ ⎠
2xy + x2y´ − y2 − 2x yy´ − 2x + 2yy′ = 0 ⇒ x2y′ − 2xyy´ + 2yy´ = − 2xy + y2 + 2x
− 2xy + y2 − 2x
y ⎡x2 − 2xy + 2y ⎤ − 2xy + y2 + 2x ⇒ y´ =
⎢ ⎥
⎣ ⎦ x2 − 2xy + 2y
110). x3 y + xy3 = 2 ⇒ 3xy + x3y´ + y3 + 3x y2y´ = 0

− ⎛ 3xy + y3 ⎞
⎜ ⎟
y´ ⎡x3 + 3xy2 ⎤ = − 3xy − y3 ⇒ y´ = ⎝ ⎠
⎢ ⎥
⎣ ⎦ x3 + 3xy2

111). x2 − xy + y2 = 3 ⇒ 2x − y − xy ′ + 2yy ′ = 0
y − 2x
− xy ′+2yy ′ = y − 2x ⇒ (2y − x ) y´ = y − 2x ⇒ y´ =
2y − x

43


112) y ´ =
y − 2x
⇒ y´ =
( 2y − x )( y´ − 2 ) − ( y − 2x )( 2y´ − 1)
2y − x ( 2y − x )
2

y´ =
( 2y − x ) y´-2 ( 2y − x ) − y ( 2y′ − 1) + 2 x ( 2y′ − 1)
( 2y − x )
2

2yy′ − xy´-4y + 2x − 2yy′ + y + 4 xy ′ − 2 x
y′ =
( 2y − x )
2

y´ =
( 2y − x − 2y + 4x ) y´ − 3y =
3x y´ − 3y
=
(y − 2x)(3x − 3y)
( 2y − x ) 2 ( 2y − x ) 2
( 2y − x ) 2 (2y − x)
3xy − 6x 2 − 6y 2 + 3xy 6 ( xy − x − y )
2 2
18
y´ = = =−
( 2y − x ) 3
( 2y − x ) 3
( 2y − x ) 3
113)3x 4 y 2 − 7xy 3 = 4 − 8y ⇒ 12x 3 y 2 + 6x 4 yy´ + 7y 3 + 27xy 2 y´ − 8y
12x 3 y 2 + 7y 3
2x 3 y 2 + 7y 3 = 8y´ − 6x 4 yy´ − 21xy 2 y ⇒ = y´
8 − 6x 4 y − 21xy 2

( ⎢
⎣
)
114) 3 − 3 ln ⎡ y 2 + 1 − 3 ln x ⎤ + 3 +
⎥
⎦
( ) ( ) (
3 ln ⎡ y 2 + 1 + 3 ln x ⎤ = c
⎢
⎣ ⎥
⎦
)
1− 3 1+ 3
2yy´ + 2yy´
( 3− 3 ) x + 3+ 3 x =0 ( )
y 2 + 1 − 3 ln x
( y )
2 + 1 + 3 ln x
( )
2xyy ´ + 1 − 3 ( ) 2xyy´ + 1 + ( 3 )
(3 − 3 ) x ⎡ y =0 (
+ 3+ 3 ) x ⎡y
⎣
+ 1 − 3 ln x ⎤
2
⎦ ( ⎣
2
)
+ 1 + 3 ln x ⎤
⎦ ( )
( ) ( ) (
3 − 3 ⎡ y + 1 + 3 ln x ⎤ ⎡ 2xyy´ + 1 − 3 ⎤ + 3 + 3 ⎡ y + 1 − 3 ln x ⎤ ⎡ 2xyy´ + 1 + 3 ⎤ = 0
⎣
2
⎦⎣ ⎦ ⎣
2
⎦⎣ ⎦ ) ( ) ( ) ( )

2xyy´ 3 − ( ) ( )
3 ⎡ y 2 + 1 + 3 ln x ⎤ + 3 − 3 1 − 3 ⎡ y 2 + 1 + 3 ln x ⎤ + (*)
⎣ ⎦ ⎣ ⎦ ( )( ) ( )
( ) (
(*) 2xyy´ 3 + 3 ⎡ y 2 + 1 − 3 ln x ⎤ + 3 + 3 1 + 3 ⎡ y 2 + 1 − 3 ln x ⎤ = 0
⎣ ⎦ ⎣ ⎦ ) ( )( ) ( )

⎣{ (
2xyy´ y 2 ⎡ 3 − ) ( 3 )⎤ + ⎣(3 − 3 )(1 + 3 ) + (3 + 3 )(1 − 3 )⎤ ln x} =
3 + 3+
⎦
⎡
⎦

{ (
− y2 ⎡ 3 −
⎣
3 )(1 − 3 ) + ( 3 + 3 )(1 + 3 ) ⎤ + ⎡( 3 − 3 )(1 − 3 )(1 + 3 ) + ( 3 + 3 )(1 + 3 )(1 − 3 ) ⎤ ln x}
⎦ ⎣ ⎦

− (12y 2 − 12 ln x ) 12 ( ln x − y 2 ) ln x − y 2
y´ = = =
2xy ( 6y 2 ) 12xy 3 xy 3

44


f. Derivación logarítmica.
Este método consiste en aplicar Logaritmos en ambos lados de la ecuación, luego

se utilizan las propiedades logarítmicas y después, los teoremas sobre

derivación, para determinar la primera derivada.

x (1 − x 2 )
2
1
115) y = ⇒ Lny = Ln x + 2Ln (1 − x 2 ) − Ln (1 + x 2 )
(1 + x )
1
2 2
2

1 1 2 x 1 1 − 4x x
2 (
y´ = + − 2x ) − ⇒ y´ = + −
x 1− x 2 (1 + x ) 1− x 2 (1 + x 2 )
2 2
y y x

x (1 − x 2 )
2
⎡1 4x x ⎤ ⎡1 4x x ⎤
y´ = y ⎢ − − ⎥ ⇒ y´ = ⎢ − − ⎥
⎢x 1 − x 2 (1 + x 2 ) ⎥ (1 + x 2 ) 2 ⎢x 1 − x 2 (1 + x 2 ) ⎥
2 1 2
⎣ ⎦ ⎣ ⎦
3
⎡ 2x − 1 ⎤
⎢(1 − 2x) e ⎡ ( 2x − 1) − 2Lnx − 1 Ln( 2−3x)⎤
1/2
⎥
116)F(x) = Ln ⎢ ⎥ ⇒ F(x) = 3⎢Ln (1− 2x) + Lne ⎥
⎢ x2 2 − 3x ⎥ ⎢
⎣ 2 ⎥
⎦
⎣ ⎦

F´(x) =3⎢
⎡ ( −2) 1
+ ( 2x − 1)−1/2 ( 2) − −
2 ( −3) ⎤ ⇒ F´(x) = 3⎡ −2 +
⎢ 1 2
− +
3
⎤
⎥
⎥
⎣ (1 − 2x) 2 x 2 ( 2 −3x) ⎦ ⎢(1 − 2x) ( 2x − 1)1/2 x 2 ( 2 − 3x) ⎥
⎣ ⎦
⎡⎛ −2 + 2 2x − 1 1/2 ⎞
F´(x) = 3⎢⎜
( ) ⎟ − ⎛ 4 ( 2 − 3x) + 3x ⎞⎤ ⎥
⎜
⎜ 2x ( 2 −3x) ⎟⎥ ⎟
⎢⎜ (1 − 2x) ⎟ ⎝ ⎠⎦
⎣⎝ ⎠
1
117)y = (1 + x) ⇒ Lny = Ln (1 + x) ⇒ Lny = Ln (1 + x)
1/x 1/x

x
y´ 1 1 ⎡ 1 ⎤ y´ 1 ⎡ Ln (1 + x) 1 ⎤ 1/x 1 ⎡ Ln (1 + x) 1 ⎤
= − Ln (1+ x) + ⎢ ⎥⇒ y = x ⎢ + ⎥ ⇒ y´=(1 + x) ⎢ + ⎥
y x2 x ⎣1 + x ⎦ ⎣ x 1 + x⎦ x⎣ x 1 + x⎦

( ) ( ) ( )
1 1
1
118) y = 1 − x2 x2
⇒ Lny = Ln 1 − x2 x2
⇒ Lny = Ln 1 − x2
x2

y′ −2
=
y x3 (
Ln 1 − x2 + ⎜
x ⎝
)
1 ⎛ −2x ⎞ y′ −2
⎟⇒ =
2 ⎜ 1 − x2 ⎟ y x3
⎠
Ln 1 − x2 −
2
x (1 − x2)
( )
(
y′ = − 2 1 − x
1
⎡ Ln 1 − x2
2 x2 ⎢
) +
1
⎤
⎥ ( )
⎢
⎢
⎣
x3 ⎥
x − x2 + 1 ⎥
⎦ ( )
45


y y
⎛1⎞ ⎛1⎞ y
⎛1⎞
119)y x ⇒ ln y = ln x
3x ⎜ ⎟ 3x ⎜ ⎟
= ⎝3⎠ ⎝3⎠
⇒ 3x ln y = ⎜ ⎟ ln x
⎝3⎠
y y y y
y´ ⎛1⎞ 1 ⎛1⎞ 1 3x y´ ⎛1⎞ 1 ⎛1⎞ 1
(3x) (ln 3) ln y + (3x ) = y´ ⎜ ⎟ ln .ln x + ⎜ ⎟ ⇒ − y´ ⎜ ⎟ ln .ln x = ⎜ ⎟ − 3x ln 3.ln y
y ⎝ 3⎠ 3 ⎝ 3⎠ x y ⎝ 3⎠ 3 ⎝ 3⎠ x
⎛ x y
⎞ ⎛ 1 ⎞y ⎡⎛ 1 ⎞ y ⎤
⎛1⎞ y ⎢ ⎜ ⎟ − x3x ln 3.lny ⎥
⎜ 3 + y ⎜ ⎟ ln 3.ln x ⎟ ⎜ ⎟ − x3 ln 3.ln y
x

⎝3⎠ ⎟= ⎝ 3⎠ ⎢⎝ 3 ⎠ ⎥
y´ ⎜ ⇒ y´ = ⎣ ⎦
⎜ y ⎟ x ⎛1⎞
y

⎜ ⎟ y 3x + y ⎜ ⎟ ln3.ln x
⎝ ⎠ ⎝3⎠
1
Cos x 1 (Cos x) 2
120) y = Cos x a ⇒ Ln y = Ln ( Cos x ) 2
+ Ln a
1 y′ 1 Sen x 1 −1
Ln y = Ln Cos x + Cos x Ln a ⇒ =− + ( Cos x ) 2 ( − Sen x ) Ln a
2 y 2 Cos x 2
⎡ ⎤
y′ 1
= − tg x +
( − Sen x ) Ln a ⇒ y′ = y ⎢ − 1 tg x − Sen x
Ln a ⎥
y 2 2 Cos x ⎢ 2 −1 ⎥
⎢
⎣ 2 Cos x ( Cos x ) 2 ⎥
⎦
⎡ ⎤
⎢ − 1 tg x − tg x ⎡ 1 tg x ⎤
y′ = y Ln a ⎥ ⇒ y′ = y ⎢ − tg x − Cos x Ln a ⎥
⎢ 2 −1 ⎥ ⎣ 2 2 ⎦
⎢
⎣ 2 ( Cos x ) 2 ⎥
⎦

y
y′ = − tg x ⎡1 − Cos x Ln a ⎤ ⇒ y′ =
− ( Cos x a Cos x
) tg x ⎡1 − Cos x Ln a ⎤
2 ⎣ ⎦ 2 ⎣ ⎦

y′ ⎡ 1 ⎛ 1 ⎞⎤
121)y = ( arc tg x )
y
→ Ln y = y Ln arc tg x ⇒
= y′ Ln arc tg x + y ⎢ ⎜ 2 ⎟⎥
y ⎣ arc tg x ⎝ 1 + x ⎠⎦
y′ y ⎡1 ⎤ y
= y′ Ln arc tg x + ⇒ y′ ⎢ − Ln arc tg x ⎥ =
y (1 + x ) arc tg x
2
⎣y ⎦ (1 + x ) arc tg x
2

y y
y′ =
(1 + x ) arc tg x ⇒ y′ = (1 + x ) arc tg x
2 2
→ ⇒ y′ =
y2
1 1 − y Ln arc tg x ⎡ (1 + x 2 ) arc tg x ⎤ [1 − y Ln arc tg x ]
− Ln arc tg x ⎢ ⎥
y y ⎣ ⎦

y y 1 xy′
122)x = yx ⇒ Ln x = Ln y x ⇒ y Ln x = x Ln y ⇒ y′ Ln x + y = Ln y +
x y
y x y′ xy′ y ⎛ x⎞ y
y′ Ln x + = Ln y + ⇒ y′ Ln x − = Ln y − ⇒ y′ ⎜ Ln x − ⎟ = Ln y −
x y y x ⎝ y⎠ x
46


y x Ln y − y
Ln y − y ( x Ln y − y )
y′ = x ⇒ y′ = x ⇒ y′ =
Ln x −
x y Ln x − x x ( y Ln x − x )
y y
'
⎛y⎞ ⎛ 2 ⎞
2 '
⎛y⎞ 1
⎜ ⎟ 1 ⎜ (x + y ) ⎟
123) arc tg ⎜ ⎟ = Ln ( x + y ) ⇒
2 2 ⎝x⎠ = ⎜ 2
⎝x⎠ 2 ⎛ y⎞
2
2 ⎜ ( x + y2 ) ⎟
⎟
1+ ⎜ ⎟ ⎝ ⎠
⎝x⎠
y′ x − y 1 ⎛ 2x + 2 y y′ ⎞ 1 y′ x − y 2(x + y y′)
= ⎜ 2 ⎟ ⇒ 2 =
⎛ ⎛ y ⎞ ⎞ 2 2 ⎝ (x + y ) ⎠
⎜ ⎟ x +y 2 ( x 2 + y2 )
2
2 2
x2
⎜1 + ⎜ ⎟ ⎟ x
⎜ ⎝x⎠ ⎟
2
x
⎝ ⎠
x 2 (y′ x − y) 2 (x + y y′) y′ x − y x + y y′ x + yy′
= ⇒ = ⇒ y′ x − y = 2 ( x 2 + y2 )
x 2 ( x 2 + y2 ) 2 ( x 2 + y2 ) ( x 2 + y2 ) ( x 2 + y2 ) ( x + y2 )
y+x
y′ x − y y′ = y + x ⇒ y′ = (x − y) = y + x ⇒ y′ =
x−y

Sen ( Ln x ) Sen ( Ln x )
⎛ x2 + b ⎞ ⎛ x2 + b ⎞ ⎛ x2 + b ⎞
124) y = ⎜ 2 ⎟ ⇒ Ln y = Ln ⎜ 2 ⎟ ⇒ Ln y = ( Sen (Ln x) ) Ln ⎜ 2 ⎟
⎝ x ⎠ ⎝ x ⎠ ⎝ x ⎠
y′ ⎡1⎤ ⎛ x2 + b ⎞ 1 ⎡ ( 2x ) x 2 − ( x 2 + b ) 2x ⎤
= Cos ( Ln x ) ⎢ ⎥ Ln ⎜ ⎟ + ( Sen ( Ln x ) ) 2 ⎢ ⎥
y ⎣x⎦ ⎝ x ⎠
2
⎛x + b⎞⎢ x2 ⎥
⎜ 2 ⎟⎣ ⎦
⎝ x ⎠
y′ Cos ( Ln x ) ⎛ x 2 + b ⎞ ( Sen Ln x ) x 2 ⎛ 2x 3 − 2x 3 − 2xb ⎞
= Ln ⎜ ⎟+ ⎜ ⎟
y x ⎝ x ⎠
2
x2 + b ⎝ x4 ⎠
⎛ x2 + b ⎞
Ln ⎜ ⎟ Cos ( Ln x )
y′ Cos ( Ln x ) ⎛ x 2 + b ⎞ Sen ( Ln x ) ( −2xb ) Sen ( Ln x ) ( −2b )
2
y′ ⎝ x ⎠
= Ln ⎜ ⎟+ ⇒ = +
y x ⎝ x ⎠
2
x +b
2
x 2
y x ( x2 + b) x
⎛ 1⎞ ⎡ ⎛ x + b ⎞
2
−2b Sen ( Ln x ) ⎤
y′ = y ⎜ ⎟ ⎢ Ln ⎜ ⎟ Cos ( Ln x ) ⎥
⎝ x ⎠⎣ ⎝ x ⎠
2
x2 + b ⎦
Sen ( Ln x )
⎛ x2 + b ⎞ ⎛ 1⎞ ⎡ ⎛ x + b ⎞
2
−2b Sen ( Ln x ) ⎤
y' = ⎜ ⎟ ⎜ ⎟ ⎢ Ln ⎜ ⎟ Cos ( Ln x ) ⎥
⎝ x ⎠
2
⎝ x ⎠⎣ ⎝ x ⎠
2
x2 + b ⎦

47


125)X a Y b = ( X + Y )
a +b
⇒ a Lnx + bLny = (a + b) Ln (x + y)
a b y' ⎛ a + b ⎞ ⎡ a b y' ⎤
+ =⎜ ⎟ (1 + y' ) ⇒ ( x + y ) ⎢ + ⎥ = ( a + b )(1 + y')
x y ⎝x+y⎠ ⎣x y ⎦
⎛x+y⎞ b y' ( x + y ) b y' ( x + y ) ⎛x+y⎞
⎜ ⎟a + = ( a + b ) + ( a + b ) y' ⇒ − ( a + b ) y' = ( a + b ) − ⎜ ⎟a
⎝ x ⎠ y y ⎝ x ⎠
⎛x+y⎞
⎡ ⎛ ( x + y) ⎞ ⎤ (a + b) − ⎜ ⎟a
⎛x+y⎞ ⎝ x ⎠
y' ⎢ b ⎜ ⎟ − ( a + b )⎥ = ( a + b ) − ⎜ ⎟ a ⇒ y' =
⎣ ⎝ y ⎠
⎢ ⎥
⎦ ⎝ x ⎠ ⎛ ( x + y) ⎞
b⎜ ⎟ − (a + b)
⎝ y ⎠
ax + bx − ax − ay
x (bx − ay) y y
y' = ⇒ y' = → y' =
bx + by − ay − by x (bx − ay) x
y
⎛ x2 + a2 + x ⎞
126).y = Ln ⎜ ⎟ ⇒ y = Ln( x 2 + a 2 + x) − Ln( x 2 + a 2 − x)
⎜ x2 + a2 − x ⎟
⎝ ⎠
( x 2 + a 2 + x)1 ( x 2 + a 2 − x)1
y' = −
x2 + a2 + x x2 + a2 − x
⎛1 2 2 −1/2 ⎞ ⎛1 2 2 −1/2 ⎞
⎜ (x + a ) (2x) + 1⎟ ⎜ (x + a ) (2x) − 1⎟
2
y' = ⎝ ⎠−⎝2 ⎠
( x + a + x)
2 2
( x + a − x)
2 2

x ( x2 + a2 ) +1 x ( x2 + a2 ) −1
−1/2 −1/2

y' = −
x2 + a2 + x x2 + a2 − x

y' =
( ⎣ ) ⎥
⎦ ⎢
⎣ (
x 2 + a 2 − x ⎡ x ( x 2 + a 2 ) + 1⎤ − x 2 + a 2 + x ⎡ x ( x 2 + a 2 ) − 1⎤
⎢
−1/2 −1/2
)
⎥
⎦
(x + a − x )
2 2 2

x + x2 + a2 − x2 ( x2 + a2 ) − x − x + x2 + a2 − x2 ( x2 + a2 )
−1/2 −1/2
+x
y' = 2
a
2 ⎡ x2 + a2 − x2 ( x2 + a )
2 −1/2 ⎤ 2 ⎡( x 2 + a 2 ) − x 2 ( x 2 + a 2 ) ⎤
−1/2 −1/2

⎢ ⎥ ⎢ ⎥
y' = ⎣ ⎦ ⇒ y' = ⎣ ⎦
a2 a 2

2 ( x2 + a2 )
−1/2
⎡x2 + a2 − x2 ⎤
⎣ ⎦ ⇒ y' = 2
y' = 2
a x2 + a2

48


Senx
127)y = ⎡ Tg ( 3x ) ⎤
⎣ ⎦ ⇒ Lny = Senx Ln (Tg(3x))
y' Cosx Ln (Tg(3x)) Senx Sec 2 (3x) y' 1 ⎡ 6Senx ⎤
= + ⇒ = ⎢Cosx Ln (Tg(3x)) + Senx (3x) (Cos(3x)) ⎥
y 2 Senx Tg(3x) y 2 Senx ⎣ ⎦
Sec 2 (3x) Sec(3x)Sec(3x) 1
NOTA: = =
Tg(3x) Tg(3x) Sen(3x) Cos (3x)
Senx ⎡ 6Senx ⎤
⎡Tg ( 3x ) ⎤
⎣ ⎦ ⎢Cosx Ln (Tg(3x)) + Senx (3x) (Cos(3x)) ⎥
y= ⎣ ⎦
2 Senx
x
128)y = x y Ln ⎛ arc sen 1 − y 2 ⎞ ⇒ y = x y x Ln ⎛ arc sen ⎞
1 − y2 ⎟
⎜ ⎟ ⎜
⎝ ⎠ ⎝ ⎠
⎛ ⎞
y = x y + 1 Ln ⎜ arc sen 1 − y2 ⎟
⎝ ⎠
'
( )
' ⎡ ⎛ ⎞⎤
y′ = x y + 1 Ln arc sen 1 − y 2 + x y + 1 ⎢ Ln ⎜ arc sen 1 − y2 ⎟ ⎥
⎣ ⎝ ⎠⎦
Por partes:z = x y + 1 ⇒ Ln z = ( y + 1 Ln x)
z'
=
y′
Ln x +
( y +1 ) → z′ = x
⎛
⎜
⎜
⎝
⎟
⎠ ⎢
(
y + 1⎟ ⎡ x y′ Ln x + 2 y
⎞
)( y +1 ⎤
⎥
)
z 2 y x ⎢ 2x y ⎥
⎣ ⎦

z′ =
(x
y
(
x) xy′ Ln x + 2 y ( )( y +1 ) ) ⇒ z′ = x y ⎡
⎣ (
xy′ Ln x + 2 y )( y +1 ⎤
⎦ )
2x y 2 y
⎡ ⎤
⎢ ⎥
1 ⎢ 1 2 y y′ ⎥
w = Ln arc sen 1 − y 2 ⇒ w′ = ⎢ ⎥
arc sen 1 − y 2 ⎢ 1 − y2 ⎥
⎢ 1− 1− y
⎣
2 2 2
( ) ⎥
⎦
1 2 y y′ 1 y y′
w′ = ( ) ⇒ w′ =
arc sen 1 − y 2 2 1 − 1 − y 2 1 − y 2 ( )
arc sen 1 − y2 y 1 − y2

1 y′ y +1
w′ = ⇒ y′ = z′ Ln arc sen 1 − y2 + x w′
arc sen 1 − y 2 1 − y2

49


'
yx
( x y ) + ⎛ e y ⎞ = ( x y )' ⇒ ( x y ) = A ; ⎛ e y ⎞ = B ; ( x y ) = C
' x x
129) x y + e = x y ⇒ Ec (*)⎜
⎝
⎟
⎠
⎜
⎝
⎟
⎠
A′ y
A = x y ⇒ Ln A = Ln x y ⇒ Ln A = y Ln x ⇒ = y ′ Ln x +
A x
⎛ y⎞ ⎛ y⎞
A′ = A ⎜ y ′ Ln x + ⎟ ⇒ A′ = x y ⎜ y ′ Ln x + ⎟
⎝ x⎠ ⎝ x⎠
yx ⎛ 1 ⎞ ⎛ B′ ⎞ x y′
B = e ⇒ Ln B = y x Ln e ⇒ Ln B = y x ⇒ Ln (Ln B) = x Ln y ⇒ ⎜ ⎟ ⎜ ⎟ = Ln y +
⎝ Ln B ⎠ ⎝ B ⎠ y
⎛ x y′ ⎞ yx ⎛ x y′ ⎞
B ′ = B LnB ⎜ Ln y + ⎟⇒ B ′ = y x e ⎜ Ln y + ⎟
⎝ y ⎠ ⎝ y ⎠
C = xy ⇒ C′ = y + x y′
⎡ y⎤ ⎡
yx x y′ ⎤
Sust en la ec (*): x y ⎢ y ′ Ln x + ⎥ + y x
⎣ x⎦ e ⎢ Ln y + y ⎥ = y + x y ′
⎣ ⎦
xy y yx yx x y′
x y y ′ Ln x +
x
+ yx e Ln y + y x e y
= y + x y′

yx x y′ yx xy y
x y y ′ Ln x + y x e y
− x y′ = y − y x e Ln y −
x
yx xy y
⎡ yx
yx e x ⎤
yx
y
x y
y − yx e Ln y −
x
y ′ ⎢ x Ln x +
y
− x ⎥ = y − yx e Ln y − ⇒ y′ =
⎢ y ⎥ x yx e x
yx
⎣ ⎦ x Ln x +
y
− x
y

Arc tag Y 1 y' y' Lnx arctg y
130) y = x ⇒ Lny = arctg y Lnx ⇒ = +
2 2y 2 y (1 + y ) x

y' y' Lnx arctg y ⎛ 1 Lnx ⎞ arct y
− = ⇒ y' ⎜ − ⎟=
2y 2 y (1 + y ) x ⎜ 2y 2 y (1 + y ) ⎟ x
⎝ ⎠
arctg y
x
⎛
⎝
( ⎞
2 arctg y ⎜ y3 ⎟ (1 + y )
⎠
)2 y3 arctg y (1 + y ) ( )
y' = = y' = ⇒ y' =
y (1 + y ) − yLnx x ⎡ y (1 + y ) − yLnx ⎤ x y ⎡(1 + y ) − y Lnx ⎤
⎣ ⎦ ⎣ ⎦
2 y (3 1+ y
)

y' =
(
2y (1 + y ) arctg y )
x ⎡(1 + y ) − y Lnx ⎤
⎣ ⎦

50


y
131) x = y ArcsenX
y' y ( cosx ) Lny ( arcsenx ) y'
y Lnx = arcsenx Lnx → Lnx + = +
2 y x
1− x 2
( y
)
y'Lnx ( arcsenx ) y' ( cosx ) Lny y
− = −
2 y y x
1− x2
⎛ ⎞
xcosx Lny − y ⎜ 1 − x 2 ⎟
⎛ Lnx arcsenx ⎞ ⎝ ⎠
y' ⎜ − ⎟=
⎜2 y y ⎟ 2
⎝ ⎠ x 1− x
⎛ ⎞
xcosx Lny − y ⎜ 1 − x 2 ⎟
⎝ ⎠ ⎡ ⎛ ⎞⎤
2 y3 ⎢ x cosx Lny − y ⎜ 1 − x 2 ⎟ ⎥
y' = x 1− x2 ⇒ y' = ⎣ ⎝ ⎠⎦
yLnx − 2 y arcsenx
(
x 1 − x 2 y Lnx − 2 y arcsenx )
2 y3

y' = ⎣ (
2 y 3 ⎡ xcosx Lny − y 1 − x ⎤ )
⎦ ⇒ y' = (
2y ⎡ xcosx Lny − y 1 − x ⎤
⎣ ⎦ )
⎛
(
⎞
y ⎜ x 1 − x 2 ⎟ y Lnx − 2arcsenx
⎝ ⎠
) ⎛
⎝
2⎞
(
⎜ x 1 − x ⎟ y Lnx − 2arcsenx
⎠
)
1
y y −x −x
⇒ Ln ⎛ x yx ⎞ = Ln ⎡ex − y − 2 ⎤
y y
132) x yx = ex − y − 2 ⎜ ⎟ ⎢ ⎥
⎝ ⎠ ⎣ ⎦
1⎡ −x 1 1 −x
Ln x + Ln yx ⎤ = Ln ⎡ex − y − 2 ⎤ ⇒ (y)Ln x + (x)Ln y = Ln ⎡ex − y − 2 ⎤
y
y⎢⎣ ⎥
⎦ ⎢
⎣ ⎥
⎦ y y ⎢
⎣ ⎥
⎦
xLn y ⎡ −x⎤
Ln x + = Ln ⎢ex − y − 2 ⎥
y ⎣ ⎦
⎛ 1 ⎞
⎜ Ln y + x y y′ y − ( x Ln y ) ( y′) ⎟ ⎡(1 − y′) e(x − y) − 2− x Ln2( −1)⎤
1 ⎝ ⎠ =⎣ ⎦
+ −x
e −2
2 x−y
x y

1 ⎡ ( Ln y + x y′− ( x Ln y) ( y′)) ⎤ ⎣(1 − y′) e + 2 Ln2⎦
⎡ ⎤
x−y −x

+⎢ ⎥= −x
e −2
x−y
x ⎢
⎣ y2 ⎥
⎦

51


⎡ y 2 + x ( Ln y + x y′ − ( x Ln y ) ( y ′) ) ⎤
⎢ ⎥ = (1 − y′ ) e x − y + 2 − x Ln 2
⎢ x y2 ⎥ e
x−y
− 2− x
⎣ ⎦
(e x−y
− 2 − x ) ⎡ y 2 + x Ln y + x 2 y ′ − ( x 2 Ln y ) ( y ′) ⎤ = x y 2 ⎡ (1 − y′ ) e x − y + 2 − x Ln 2 ⎤
⎣ ⎦ ⎣ ⎦
(e x−y
− 2 ) ⎣ y + xLny + x y ′ − ( x Ln y ) ( y ′) ⎦ = xy e − y'xy e + xy 2 Ln2
−x
⎡ 2 2 2
⎤ 2 x−y 2 x−y 2 −x

x 2 y'
e x − y y 2 + e x − y xLny + x 2 y'e x − y − e x − y ( x 2 Ln y ) ( y ′) − y 2 2 − x − xlny2 − x − 2 − x = (*)
y
(*) xy 2 e x − y − y'xye x − y + xy 2 2 − x Ln2

⎡ x 2 ex−y 2−x x 2 ⎤
y' ⎢ − e x − y ( x 2 Ln y ) − + xye x − y ⎥ = xy 2 e x − y + xy 2 2 − x Ln2 − e x − y y 2 − e x − y xLny
⎣ y y ⎦

xy 2 e x − y + xy 2 2 − x Ln2 − e x − y y 2 − e x − y xLny
y' =
x 2 ex−y 2− x x 2
− e x − y ( x 2 Ln y ) ( y ′) − + xye x − y
y y

1
y
133). x x y x = e x + y + ⎛ y ⎞
2x ⇒ ⎜ x y x ⎟
x
= ex + y + 2x
⎝ ⎠

1
⎛ ⎞ 1
2 x ⎤ ⇒ ⎡ Ln x + Ln y x ⎤ = Ln ⎣ e x + y +
y y
= Ln ⎡ e x + y +
x
Ln ⎜ x yx ⎟ ⎡ ⎤
2x ⎦
⎝ ⎠ ⎢
⎣ ⎥
⎦ x⎣⎢ ⎥
⎦

y x ⎛ y⎞
Ln x + Ln y = Ln ⎡ e x + y + 2 x ⎤ ⇒ ⎜ ⎟ Ln x + Ln y = Ln ⎡ e x + y +
⎣ 2x ⎤
⎦
x x ⎢
⎣ ⎥
⎦ ⎝x⎠

⎛ y′ x + y ⎞ y⎛1⎞ y′ 1
⎜ ⎟ Ln x + ⎜ ⎟ + = ⎡ (1 + y ′ ) e x + y + 2 x Ln 2 ⎤
⎡e 2x ⎤ ⎣ ⎦
2
⎝ x ⎠ x⎝x⎠ y ⎣
x+ y
+ ⎦

( y′ x + y ) Ln x + y
+
y′
=
1
⎡ (1 + y ′ ) e x + y + 2 x Ln 2 ⎤
⎡e 2 ⎤ ⎣ ⎦
2
x y ⎣
x+ y
+ x
⎦

y ⎡ ( y ′ x + y ) Ln x + y ⎤ + x 2 y ′ (1 + y ′ ) e x + y + 2 x Ln 2
⎣ ⎦ =
x2 y e
x+ y
+ 2x

52


(e x+ y
(
+ 2 x ) ⎡ y y′ x Ln x + y 2 Ln x + y 2 + x 2 y′⎤ = x 2 y e x + y + y′ e x + y + 2 x Ln 2
⎣ ⎦ )
[ y y′ x Ln x ] ( e x + y + 2 x ) + y 2 Ln x ( e x + y + 2 x ) + y 2 ( e x + y + 2 x ) + x 2 y ' ( e x + y + 2 x ) = (*)
(*) x 2 y ( e x + y ) + y′ e x + y x 2 y + 2 x Ln 2 x 2 y

y y ′ x Ln x ( e x + y + 2 x ) + x 2 y ' ( e x + y + 2 x ) − y′ e x + y x 2 y = (**)
(**) − y 2 Ln ( e x + y + 2 x ) − y 2 ( e x + y + 2 x ) + x 2 y ( e x + y ) + 2 x Ln 2 x 2 y

y′ ⎡ y x Ln ( e x + y + 2 x ) + x 2 ( e x + y + 2 x ) − e x + y x 2 y ⎤ = (***)
⎣ ⎦
(***) − y 2 Ln x ( e x + y + 2 x ) − y 2 ( e x + y + 2 x ) + x 2 y ( e x + y ) + 2 x Ln 2 x 2 y
− y 2 Ln x ( e x + y + 2 x ) − y 2 ( e x + y + 2 x ) + x 2 y ( e x + y ) + 2 x Ln 2 x 2 y
y′ =
y x Ln x ( e x + y + 2 x ) + x 2 ( e x + y + 2 x ) − e x + y x 2 y

g. Ejercicios Varios
1−x
e
134) Demostrar que la derivada de F ( x ) = LN ⎡ e2x ⎤
⎥ es F ′(x) = 1 +
⎢
⎢ 1 −e
⎣
1− x
⎥
⎦
(
2 1 − e1−x )
⎡ ⎤
F(x) = Ln ⎢
e 2x
(1 − x)
⎥⇒ y =
1
2
[ (
1
)]
Ln e 2x − Ln 1 − e1 − x ⇒ y = 2x − Ln 1 − e1 − x
2
[ ( )]
⎢ 1−e
⎣ ⎥
⎦

2 −
(
1 − e1 − x (−1) )
1 − e1 − x e1 − x
y´ = ⇒ y´ = 1 +
2 2 1 − e1 − x ( )
x3 x + 1 5x + 3
135) Demostrar que la derivada de Ln , es y ' = − csc x sec x.
Senx Secx 6 x (x + 1)
Lnx 1
y= + Ln(x + 1) − (Ln Senx + Ln Secx )
2 3
1 1 ⎛ Cosx Secx Tgx ⎞ 3x + 3 + 2x ⎛ Cosx 2 + Senx 2 ⎞
y' = + −⎜ + ⎟ → y' = −⎜ ⎟
2x 3(x + 1) ⎝ Senx Secx ⎠ 6x(x + 1) ⎜
⎝ Senx Cosx
⎟
⎠
5x + 3 1 5x + 3
y' = − ⇒ y' = − cscx secx
6x(x + 1) Senx Cosx 6x(x + 1)

53


136) Demostrar que la derivada de y = x π 2 − x 2 ; es y´= 2 π 2 − x 2
x( −2x) (π2 − x2 )
−1/2
π2 ⎛ 1 ⎞ π
y' = (π − x ) +
2 2 1/2
+ ⎜ ⎟ ⇒ y ' = ( π − x ) − x (π − x ) + 2 2
2 2 1/2 2 2 2 −1/2

2 x2 ⎝ π ⎠ π −x
1− 2
π π
y' = (π2 − x2 ) − x2 (π2 − x2 ) +π2 (π2 − x2 ) ⇒ y' = (π2 − x2 ) ⎡(π2 − x2 ) − x2 +π2 ⎤ ⇒
1/2 −1/2 −1/2 −1/2

⎣ ⎦
y' = (π2 − x2 ) ⎡π2 − x2 − x2 +π2 ⎤ ⇒ y' = (π2 − x2 ) 2(π2 − x2 ) ⇒ y`= 2 π2 − x2
−1/2 −1/2
⎣ ⎦

137) Demuestre que: f (x) =
⎡ a−b 1⎛ x ⎞⎤ 1
Arctg ⎢ Tg ⎜ ⎟⎥ ⇒ f ′(x) =
a2 − b 2 ⎢ a+b
⎣ ⎝ 2 ⎠⎦
⎥ 2 [a + b Cosx]
⎛ ⎞⎛ a − b 2⎛ x⎞
⎞
1 ⎡ a −b ⎛ x⎞ ⎤ 1 ⎜ 1 ⎟ ⎜ a + b Sec ⎜ 2 ⎟ ⎟
f ( x) = Arctg ⎢ Tg ⎜ ⎟ ⎥ ⇒ f '( x) = ⎜ ⎟⎜ ⎝ ⎠⎟
a −b
2 2
⎣ a+b ⎝ 2 ⎠⎦ a − b ⎜1+ ⎛
2 2 a − b ⎞ 2 ⎛ x ⎞ ⎟⎜ 2 ⎟
⎜ ⎜ a + b ⎟ Tg ⎜ 2 ⎟ ⎟⎜ ⎟
⎝ ⎝ ⎠ ⎝ ⎠ ⎠⎝ ⎠
⎛ ⎛x⎞ ⎞
⎜ a − b Sec 2 ⎜ ⎟ ⎟
⎜ ⎝2⎠ ⎟ ⎛x⎞
(a + b) a − b Sec 2 ⎜ ⎟
1 ⎜ 2 a+b ⎟ ⎝2⎠
f '( x) = ⇒ f '( x) =
2 ⎜ ⎛x⎞⎟ ⎡
a − b ⎜ (a + b) + (a − b) Tg 2
2
⎛ x ⎞⎤
⎜ ⎟⎟ 2 a 2 − b 2 a + b ⎢(a + b) + (a − b) Tg 2 ⎜ ⎟ ⎥
⎜ ⎝2⎠ ⎟ ⎣ ⎝ 2 ⎠⎦
⎜ ( a + b) ⎟
⎝ ⎠

⎛ x⎞ ⎛ x⎞
(a + b) 2 (a − b) Sec 2 ⎜ ⎟ Sec 2 ⎜ ⎟
f '( x) = ⎝2⎠ ⇒ f '( x) = ⎝2⎠
⎡ ⎛ x ⎞⎤ ⎡ ⎛ x ⎞⎤
2 (a − b)(a + b)(a + b) ⎢(a + b) + (a − b)Tg 2 ⎜ ⎟ ⎥ 2 ⎢ (a + b) + (a − b) Tg 2 ⎜ ⎟ ⎥
⎣ ⎝ 2 ⎠⎦ ⎣ ⎝ 2 ⎠⎦

1 1
f '( x) = ⇒ f'(x) =
⎡ ⎛ x ⎞⎤ ⎛ x⎞ ⎡ ⎛x⎞ ⎛x⎞ ⎛ x ⎞⎤
2 ⎢(a + b) + (a − b) Tg 2 ⎜ ⎟ ⎥ Cos 2 ⎜ ⎟ 2 ⎢(a + b)Cos 2 ⎜ ⎟ + (a − b) Tg 2 ⎜ ⎟ Cos 2 ⎜ ⎟ ⎥
⎣ ⎝ 2 ⎠⎦ ⎝2⎠ ⎣ ⎝ 2⎠ ⎝ 2⎠ ⎝ 2 ⎠⎦

1
f'(x) =
⎡ ⎛x⎞ ⎛x⎞ ⎛x⎞ ⎛ x ⎞⎤
2 ⎢a Cos 2 ⎜ ⎟ + b Cos 2 ⎜ ⎟ + a Sen 2 ⎜ ⎟ − bSen 2 ⎜ ⎟ ⎥
⎣ ⎝ 2⎠ ⎝ 2⎠ ⎝ 2⎠ ⎝ 2 ⎠⎦

54


1 1
f'(x) = ⇒ f'(x) =
⎡ ⎡ ⎛x⎞ ⎛ x ⎞⎤ ⎡
1
⎛ x⎞ ⎛ x ⎞⎤⎤ ⎡ ⎡ ⎛x⎞ ⎛ x ⎞⎤⎤
2 ⎢a ⎢ Cos2 ⎜ ⎟ +Sen2 ⎜ ⎟⎥ + b ⎢Cos2 ⎜ ⎟ − Sen2 ⎜ ⎟⎥⎥ 2 ⎢a + b ⎢Cos2 ⎜ ⎟ − Sen2 ⎜ ⎟⎥⎥
⎢ ⎣ ⎝ 2⎠ ⎝ 2 ⎠⎦ ⎣ ⎝ 2⎠ ⎝ 2 ⎠⎦⎥ ⎣ ⎣ ⎝ 2⎠ ⎝ 2 ⎠⎦⎦
⎣ ⎦
1 1
f'(x) = ⇒ f'(x) =
⎡ ⎡ ⎛x⎞ ⎛ x ⎞⎤⎤ ⎡ ⎡ ⎛ x ⎞ ⎤⎤
2 ⎢a + b ⎢Cos2 ⎜ ⎟ −1+ Cos2 ⎜ ⎟⎥⎥ 2 ⎢a + b ⎢2Cos2 ⎜ ⎟ −1⎥⎥
⎣ ⎣ ⎝ 2⎠ ⎝ 2 ⎠⎦⎦ ⎣ ⎣ ⎝ 2 ⎠ ⎦⎦
⎛ θ ⎞ ⎛ 1+ Cosθ ⎞ 1 1 1
Pero:Cos2 ⎜ ⎟ =⎜ ⎟ ⇒ f'(x) = ⇒ f'(x) = ⇒ f'(x) =
⎝ 2⎠ ⎝ 2 ⎠ ⎡ ⎡ ⎛ 1+ Cosθ ⎞ ⎤⎤ 2[ a + b(1+ Cosθ −1)] 2[ a + bCosθ]
2 ⎢a + b ⎢2⎜ ⎟ −1⎥⎥
⎣ ⎣ ⎝ 2 ⎠ ⎦⎦

y
138) Demuestre que si x 2 y 5 = ( x + y ) , entonces y´ =
7
.
x
6
[
2 xy 5 + 5 x 2 y 4 y´ = 7 (x + y ) (1 + y´) ⇒ y´ 5 x 2 y 4 − 7 (x + y ) = 7 (x + y ) − 2 xy 5
6
] 6

7 (x + y )
6
− 2 xy 5
y´ =
5 x 2 y 4 − 7 (x + y )
6

Multiplicando numerador y denominador por x.y:

y´ =
7 xy( x + y ) − 2 y x2 y5
6
(
=
)
7 xy(x + y ) − 2 y( x + y )
=
y( x + y ) [7 x − 2(x + y )] y(5x − 2 y ) y
6 7
=
6
=
( 2 5
)
5x x y − 7 xy(x + y )
6
5x( x + y ) − 7 xy( x + y )
7 6
x( x + y ) [5(x + y ) − 7 y] x(5x − 2 y ) x
6

xy y2 + x2
139) Demostrar que y' = es la derivada de y = arctg
y y 4 − x 4 + x2 y2 − x2

( 2yy' + x )( y
2 2
− x 2 ) − ( y 2 + x 2 )( 2yy' − x 2 )
(y − x2 )
2 2
1
y' =
⎛ y2 + x 2 ⎞ ⎛ y2 + x 2 ⎞
1+ ⎜ 2 2 ⎟ 2 ⎜ 2 2 ⎟
⎝ y −x ⎠ ⎝ y −x ⎠

55


2y3y' − 2x2 yy' + 2xy2 − 2x3 − 2y3y' + 2xy2 − 2x2yy' + 2x3 −4y2 yy' + 4xy2

y' =
(y −x )
2 2 2

⇒ y' =
(y −x )
2 2 2

⎛ y2 − x2 + y2 + x2 ⎞ ⎛ y2 + x2 ⎞ ⎛ y2 ⎞ ⎛ ⎛ y2 + x2 ⎞ ⎞
2⎜ ⎟ ⎜ 2 2⎟ 2⎜ 2 2 ⎟ ⎜ ⎜ 2 2 ⎟ ⎟
⎝ y2 − x2 ⎠ ⎝ y −x ⎠ ⎜ ⎟
⎝ y − x ⎠⎝ ⎝ y − x ⎠ ⎠
−4y2 yy' + 4xy2

y' =
( y − x ) ⇒y' = ( −4x yy' + 4xy )( y − x ) y − x
2 2 2 2 2 2 2 2 2

2( 2y ) y + x
2 2
4y y + x ( y − x )
2 2 2 2 2 2 2

(y −x ) y −x
2 2 2 2

( −4x yy' + 4xy ) ( y − x )
2 2
−4x yy' + 4xy
2 2 3
4y ( xy − x y') 2 2 2

y' = ⇒ y' = ⇒ y' =
4y y + x ( y − x ) 4y y + x y − x 2 2
4y ( y + x )( y − x )
2 2 2 2 2 2 2 2 2 2 2 2 2 2

( )
⇒ y' y y4 − x4 = xy − x2 y' ⇒ y' y y4 − x4 + x2 = xy ⇒ y' = ( ) xy
y y4 − x4 + x2

140) Demuestre que la derivada Lny =
2 ⎛ 4y + x ⎞
arctg⎜ ⎟ es y' = − y2
⎜ ⎟
15 ⎝ 15x ⎠ 2⎛ x 2 + y 2 ⎞
⎜ ⎟
⎝ ⎠
⎡ ⎤
y' 2 ⎢ 1 ⎥ ⎡ (4y'+1)(x ) − (4y + x ) ⎤ y' 2[(4y'+1)x − (4y + x )]
= ⎢ ⎥⎢ ⎥⇒ =
y 15 ⎢
1+
(4y + x )2 ⎥⎣ 15 x 2
⎦ y 2 15 x + (4y + x )
⎡ 2 2
⎤
⎢ ⎥ 15 x ⎢ ⎥
⎣ 15x 2 ⎦ ⎢
⎣ 15 x 2 ⎥
⎦
y' 2[(4y'+1)x − (4y + x )]
= ⇒ y' ⎛16x 2 + 16y 2 + 8xy ⎞ = 2y[4y' x + x − 4y − x]
⎜ ⎟
y 15x 2 + 16y 2 + 8xy + x ⎝ ⎠
2

y' ⎛16x 2 + 16y 2 + 8xy ⎞ = 8yy' x − 8y 2 ⇒ y' ⎛16x2 + 16y2 + 8xy − 8xy ⎞ = −8y2
⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
− 8y2 − y2
y' ⎛16x 2 + 16y2 ⎟ = −8y2 ⇒ y' =
⎜
⎞ ⇒ y' =
⎝ ⎠ 16⎛ x2 + y2 ⎞ 2⎛ x2 + y2 ⎞
⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠

56


( )
y+
1
x y( x 2 − 1)
141) Demostrar que la derivada de y = Cxe es y ' =
x(1 − y )
⎡ ( )
y+
1
x ( )⎛
y+
1
1 ⎞⎥
⎤ ( )
y+
1
( ) y+
1
C ( )
y+
1

y ' = C ⎢e
x

⎢
+ xe x
⎜ y '− 2 ⎟ ⎥ ⇒ y ' = Ce + Cxy ′e x
− 2 e x

⎝ x ⎠ x
⎢
⎣ ⎥
⎦
( )
y+
1
( ) y+
1
x
Cx 2
e x
− ce
⎡ ( )⎤y+
1
x ( ) y+
1
C
( )
y+
1
x
x2
y ' ⎢1 − Cxe ⎥ = Ce − e ⇒ y' =
x

⎢
⎢
⎣
⎥
⎥
⎦
x2 ⎡
⎢1 − Cxe
( )⎤
y+
⎥
1
x

⎢ ⎥
⎣ ⎦
⎛ 1 ⎞ y yx 2 − y
⎜
⎜y+
⎟
⎟ yx −
⎜ x ⎟
x → y' = x y( x 2 − 1)
pero y = Cxe
⎝ ⎠
⇒ y' = 2 ⇒ y' =
x [1 − y ] x 2 [1 − y ] x [1 − y ]

5(1 − y )
142) Pruebe que si e − y 1 + x 2 ( )
5/2
= cx 5 ( y − 1), entonces y ′ =
.
xy 1 + x 2 ( )
− y + ln (1+ x 2 ) = ln c + 5 ln x + ln ( y − 1) ⇒ − y ´ +
5 5x y´
= ⇒
2 1+ x 2
y −1
yy´ −5 5 (1 − y )
= ⇒ y´ = .
y − 1 x (1 + x )2
xy (1 + x 2 )

Ctg(1/x) 3Ctg(1/x) Ln3
143) Demostrar que la derivada de y = 3 es y' =
⎛1⎞
X 2 sen2 ⎜ ⎟
⎝x⎠
⎛ ⎛ 1 ⎞⎞
y = 3 Ctg(1/x) ⇒ y' = 3 Ctg(1/x) Ln3 ⎜ Ctg ⎜ ⎟ ⎟
⎜ ⎟
⎝ ⎝ x ⎠⎠
⎛ ⎛ 1 ⎞⎞ ⎛ 1 ⎞
⎟ ⇒ y' = 3 Ctg(1/x) Ln3 ⇒ y' = 3
Ctg(1/x)
Ln3
y' = 3 Ctg(1/x) Ln3 ⎜ − Csc 2 ⎜ ⎟ ⎟ ⎜ −
⎜
⎝ ⎝ x ⎠ ⎟ ⎜ x2 ⎟
⎠⎝ ⎠ ⎛ ⎛ 1 ⎞⎞
2

⎜ Xsen ⎜ ⎟ ⎟
⎜ ⎟
⎝ ⎝ x ⎠⎠
3 Ctg(1/x) Ln3
y' =
⎛1⎞
X 2 sen 2 ⎜ ⎟
⎝x⎠

57


x(m + n) − na
144) Demuestre que la derivada de y = m Lnx2 − a2 ) + mLn⎛ x − a⎞ es: y' =
( ⎜ ⎟
2 2a ⎝ x + a⎠ x2 − a2

2mx n ⎡(x + a) − (x − a )⎤
y' = + ⎢ ⎥⇒
2 ( x 2 − a 2 ) 2a ⎛ x − a ⎞ ⎢ (x + a)
2
⎥
⎜ ⎟⎣ ⎦
⎝x+a⎠
2mx n ⎡ 2a ⎤
y' = +
2 ( x 2 − a 2 ) 2a ( x − a ) ⎢ x + a ⎥
⎣ ⎦

mx n mx + n ( x − a ) x ( m + n ) − na
y' = + ⇒ y' = ⇒ y' =
x2 − a2 (x + a ) (x2 − a2 ) x2 − a2

sen x ⎛π x ⎞
145) Verifique que: si y = − ln tg ⎜ − ⎟ entonces y´ = 2 sec x.
3

cos2 x ⎝ 4 2⎠
1 sen x
sec x = , tg x = , sen 2x = 2 sen x . cos x,
cos x cos x
sen (α − β ) = sen α . cos β − sen β . cosα 1 + tg2 x = sec2 x,

⎛π x⎞
sec2 ⎜ − ⎟
⎛π x⎞ ⎝4 2⎠
y = sec x tg x − ln tg ⎜ − ⎟ ⇒ y´= sec xtg2 x + sec3 x +
⎝4 2⎠ ⎛π x⎞
2tg ⎜ − ⎟
⎝4 2⎠
1
y ′ = sec x tg2 x + sec3 x +
⎛π x⎞ ⎛π x⎞
2 sen⎜ − ⎟ cos⎜ − ⎟
⎝4 2⎠ ⎝4 2⎠
1 1
y´= sec x tg2 x + sec3 x + ⇒ y´= sec x.tg2 x + sec3 x +
⎛π ⎞ cos x
sen⎜ − x ⎟
⎝2 ⎠
( )
y´= sec xtg2 x + sec3 x + sec x ⇒ y ′ = sec3 x + sec x 1 + tg2 x y ′ = sec3 x + sec x sec2 x
y´ = sec3 x + sec3 x ⇒ y ′ = 2 sec3 x

58


146) Demuestre que y´ =
1
es la derivada de: y=2 2x +2 x+4+4 2ln
2 2− x+4 x −2 ( )( )
2x − x + 4 x−4

2 2− x+4
x −4= ( x +2 )( )
x − 2 ⇒ y = 2 2x + 2 x + 4 + 4 2 ln
x+2

y = ⎡2 2x − 4 2 ln
⎣ ( ) (
x + 2 ⎤ + ⎡2 x + 4 + 4 2 ln 2 2 − x + 4 ⎤
⎦ ⎣ ⎦ )
⎡ ⎤ ⎡ ⎤
⎢ 1 2 ⎥ ⎢ 1 2 2 ⎥
y´ = 2 ⎢ − + −
⎢
⎣
2x 2x x + 2 ( )
⎥ ⎢ x+4
⎥ ⎣
⎦
x+4 2 2− x+4 ( ) ⎥
⎦

2 ⎛ 2 ⎞ 1 ⎛ 2 2 ⎞
y′ = ⎜1 − ⎟+ ⎜1 −
⎜ ⎟
2x ⎝ x + 2⎠ x+4 ⎝ 2 2 − x + 4⎟
⎠

2 x x+4 2 1
y´ = − ⇒ y′ = −
2 2x ( x +2 ) x+4 2 2− ( x+4 ) x +2 2 2 − x + 4

y′ =
2 ( x −2 ) −
(2 2+ x+4 )
( x +2 )( x −2 ) (2 2 − x+4 ) (2 2+ x+4 )

y´ =
2 ( x −2 )+2 2+ x + 4
⇒ y′ =
2x + x + 4
⇒ y′ =
( 2x + x + 4 )( 2x − x + 4 )
x− 4 x −4 x−4 ( x − 4) ( 2x − x + 4 )
x −4 1
y′ = ⇒ y′ =
( x − 4) ( 2x − x + 4 ) 2x − x + 4

59


Senax
Cosbx 1 Sen3(ax )
147) Determine la primera derivada de y =3 +
3 Cos 3(bx )
' ⎛
( '
)( )( '⎞
)( )
Sen ax
Cos bx ⎛ Senax ⎞ ⎜ ⎛ 1 ⎞ Sen 3 (ax ) Cos 3 (bx ) − Sen 3 (ax ) Cos 3 (bx ) ⎟
y ′ =3 Ln3⎜
⎜ Cosbx ⎟ + ⎜ ⎜ 3 ⎟
⎟
⎝ ⎠ ⎜⎝ ⎠
⎝ (
Cos 3 (bx )
2
) ⎟
⎟
⎠
Sen ax
Cos bx ⎡ (a(Cos(ax ))(Cos(bx ))+ b(Sen(ax ))(Sen(bx )))⎤
y ′ =3 Ln3⎢ ⎥ + (*)
⎣ (
Cos 2 (bx ) ) ⎦
( ) (
1 ⎡ 3aSen2 (ax )Cos (ax ) Cos 3 (bx )+ Sen3 (ax ) 3bCos 2 (bx )Sen(bx ) ⎤
(*) ⎢ ⎥
)
3⎢⎣ Cos 3 (bx )
2
( ) ⎥
⎦
Sen ax

y′= 3
Cos bx
Ln3 ⎡ (aCos(ax )Cos(bx )+ bSen(ax )Sen(bx ))⎤ + (**)
⎢
⎣ (
Cos 2 (bx ) ) ⎥
⎦
1 ⎡ 3Sen2 (ax )Cos 2 (bx )[aCos(ax )Cos(bx )+ bSen(ax )Sen(bx )]⎤
(**) ⎢
3⎣ (
Cos 6 (bx ) ) ⎥
⎦
⎛ ⎞ Senax
⎜ (aCos(ax )Cos(bx )+ bSen( ax )Sen(bx )) ⎟ ⎛ Cos bx Sen2 ax ⎟
⎞
y′= ⎜ ⎟⎜ 3 Ln3+
⎜ ⎛ Cos 2 (bx )⎞ ⎟⎜⎜ Cos 2 bx ⎟
⎟
⎜ ⎜ ⎟ ⎟⎝ ⎠
⎝ ⎝ ⎠ ⎠

Nota: Los ejercicios resueltos anteriormente han sido tomados de textos, guías y
exámenes aplicados en el IUTJAA. Muchos de ellos son recopilaciones de mis
colegas y amigos Germán Narváez y Orlando Rodríguez profesores ya jubilados
en la institución, y otros resueltos por el autor.
Por favor a los lectores espero su valiosa colaboración, en la revisión de los
mismos y hacerme llegar las sugerencias y correcciones necesarias a las
direcciones electrónicas publicadas.
Gracias.
Dámaso Rojas
Octubre 2007

60

Derivadas teoria-ejercicios-resueltos

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Derivadas teoria-ejercicios-resueltos

Último

Derivadas teoria-ejercicios-resueltos