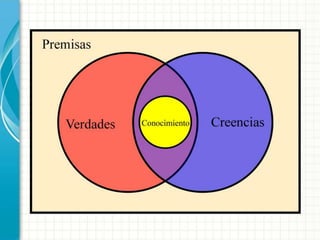
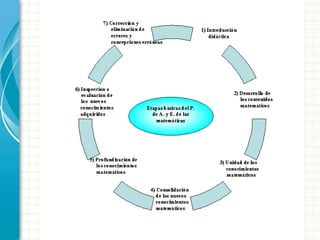
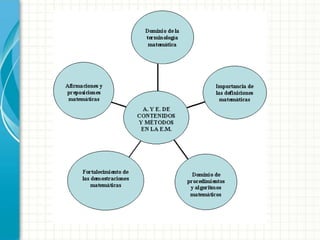
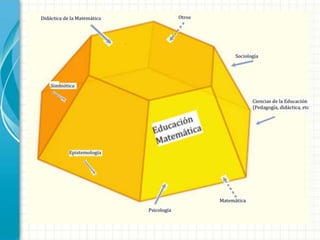
Este documento discute varios conceptos clave en epistemología y didáctica de las matemáticas. Explica que la epistemología estudia el conocimiento y su adquisición, mientras que la didáctica se enfoca en los procesos de enseñanza y aprendizaje. También explora las diferencias entre didáctica, metodología y educación matemática, y analiza varias teorías importantes en didáctica de las matemáticas como la modelización, razonamiento matemático y transposición didáctica. El

1. FUNDAMENTOS DE LA
DIDÁCTICA DE LA
MATEMÁTICA.
Roxana Vargas Wiederhold,
rvargasw@gmail.com
Primer Semestre 2013

2. Epistemología y Didáctica de la
Matemática
• La epistemología (del griego ἐπιστήμη
(episteme), "conocimiento", y λόγος (logos), "estudio") es la
rama de la filosofía cuyo objeto de
.
• La epistemología, como teoría del conocimiento, se ocupa
de problemas tales como las
que llevan a la
obtención del conocimiento, y los criterios por los cuales
se le justifica o invalida, así como la definición clara y
precisa de los conceptos epistémicos más usuales, tales
como verdad, objetividad, realidad o justificación. La
epistemología encuentra ya sus primeras formas en la
Grecia Antigua, primero en filósofos como Parménides o
Platón.

4. Epistemología y Didáctica de la
Matemática
• El rmino “ a” es parte de la ctica de la
tica a inicio de los os las diferentes
acepciones que lo an y que conducen a diversas
“definiciones” e interpretaciones en cada s y en ltiples
situaciones.
• Mientras o a Brousseau (2006a, b) para un lisis
comparado y tico de dicho rmino y de sus diversas
exigencias, hago cito el hecho que me referire, n si no lo
digo abiertamente, a estos recientes dos trabajos de Brousseau y a
otros trabajos suyos, todos estos citados en la a. Algunas
de las frases que siguen fueron tomadas libremente de estos
textos, sin cambiar el ritu
siempre los trabajos de Brousseau lo en
algunas ocasiones.

5. Epistemología y Didáctica de la
Matemática
• En nuestro campo de n:
una es un conjunto de
convicciones, de conocimientos y de saberes ficos,
que tienden a decir cuales son los conocimientos de los
individuos o de los grupos de personas, su
funcionamiento, las formas de establecer su validez, de
adquirirlas y por tanto de arlas y de aprenderlas; la
a es un tentativo de identificar y de unificar
diversas concepciones gicas relativas a una
determinada ciencia, a un determinado movimiento
gico, a grupos de personas, a instituciones o a
culturas.

6. Conceptos Claves
• Por entendemos un conjunto de conocimientos o de
actitudes reproducibles, adquiridos a s del estudios o de la
experiencia.
En el mbito de la a cognitiva se distinguen los saberes de
los conocimientos.
• Los : los saberes son datos, conceptos, procesos o
todos que existen fuera del individuo que conoce y que son
generalmente codificados en obras de
referencia, manuales, enciclopedias, diccionarios; los
conocimientos son inseparables del individuo que conoce; es
decir, no existe, un conocimiento a-personal; una persona que
interioriza un saber tomando conciencia, transforma este saber en
conocimiento.
Volvamos ahora al discurso ctico; este es amplio y puede
tener origen en varias ces, una de las cuales tiene sede en el
debate entre

7. ¿Didáctica o Metodología?
• Didáctica de la Matemática.
– La didáctica es la ciencia que se interesa por la producción y comunicación
del conocimiento. Saber que es lo que se está produciendo en una situación
de enseñanza es el objetivo de la didáctica. (Brousseau)
– la organización de los procesos de enseñanza y aprendizaje relevantes para
tal materia. Los didactas son organizadores, desarrolladores de
educación, autores de libros de texto, profesores de toda clase, incluso los
estudiantes que organizan su propio aprendizaje individual o grupal.
(Freudenthal)
– Es el Estudio de los procesos de transmisión y de adquisición de los
diferentes contenidos de esta ciencia, se propone describir y explicar los
fenómenos relativos a las relaciones entre sus enseñanza y aprendizaje. No
se reduce a buscar una buena forma de enseñar una determinada
noción.(Douady)
– La didáctica de una disciplina estudia los procesos de transmisión y de
adquisición relativos al dominio específico de esta disciplinas, o de las
ciencias cercanas con las cuales se interactúa. (Vergnaud).
– Es la disciplina científica y el campo de investigación cuyo objetivo es
identificar, caracterizar y comprender los fenómenos y los procesos que
condicionan la enseñanza y el aprendizaje de la matemática. (D’ Amore).

8. Didáctica de la Matemática
• La ctica de la tica (que para nosotros es un aspecto de la s
general n tica) es el que
pueden determinar el aprendizaje de un conocimiento tico por parte del
individuo (que puede ser un organismo cualquiera implicado en dicha actividad:
una persona, una n, un sistema, o incluso un animal).
• El aprendizaje se considera aquí como un
(por tanto de prestaciones) que alan, a un observador
predeterminado, n en juego, que este primer sujeto dispone de un
conocimiento (o de una competencia) o de un conjunto de conocimientos (o de
competencias), lo que implica la n de diversos registros de
n, la n de convicciones ficas, el uso de diversos
lenguajes, el dominio de un conjunto de referencias neas, de pruebas, de
justificaciones y de obligaciones. Estas condiciones deben poder ser puestas en
n y reproducidas intencionalmente. Se habla en este caso de cticas
cticas.4

10. Didáctica de la Matemática
• Estas son n “condiciones” y por tanto, a su
vez, objeto de estudio. La ctica se presenta entonces como el
estudio de tales convicciones, bajo forma de proyectos y de efectivas
realizaciones.
• Los -de tipo experimental- en este campo necesitan
de la n de conceptos y de todos que deben ser sometidos
a exigencias de n de la coherencia y de n a la
fica contingencia. Ciertas as, como por ejemplo la a de
las situaciones cticas, tienen por objeto evidenciar los aspectos que
estudia la ctica.
• Entre los objetos de estudio de la ctica, un papel absolutamente
fundamental, pero en ocasiones subordinado, se le asigna al medio o
entorno.

12. Educación Matemática
• La educación matemática es un término que se
refiere tanto a el aprendizaje, como la práctica y
enseñanza de las matemáticas, así como a un
campo de la sobre
esta práctica. Los investigadores en educación
matemática en primera instancia, cuestionan las
herramientas, métodos y enfoques que faciliten
la práctica y/o el estudio de la práctica.

13. Educación Matemática
• De manera más crítica la educación es más que un simple
termino, como lo expresa el ilustre pedagogo Rafael Flores Ochoa :
" es el proceso social e intersubjetivo mediante el cual cada
sociedad asimila a sus nuevos miembros según sus propias
reglas, valores, pautas, ideologías, tradiciones, practicas, proyecto
s y saberes compartidos por la mayoría de la sociedad. Más
modernamente la educación no solo socializa a los individuos sino
que también rescata en ellos lo más valioso, aptitudes creativas e
innovadoras, los humaniza y potencia como personas" (Hacia una
pedagogía del Conocimiento, 1994, pág.. 304).
• Si además le agregamos el significado de matemática, expresada
por el ilustre matemático Bruno D’ Amore, "son una construcción
humana que se utiliza con fines técnicos para la modelización de
nuestro entorno y de aplicación en la resolución de problemas
prácticos" (Didáctica de la matemática, 2006, pág. 15), la
Educación Matemática se torna compleja en si misma.

15. En Resumen
El rmino n es s amplio que ctica.
Educación Matemática Didáctica de la Matemática
Rico, Sierra y Castro (2000; p. 352) todo Rico, Sierra y Castro (2000; p. 352). La
el sistema de conocimientos, disciplina que estudia e investiga los
instituciones, planes de n y problemas que surgen en n
finalidades formativas‖ que conforman tica y propone actuaciones
una actividad social compleja y fundadas para su n.
diversificada relativa a la anza y
aprendizaje de las ticas.
En el mundo n se emplea la n "Mathematics Education" para
referirse al rea de conocimiento que en Francia, Alemania, a, etc. se
denomina ctica de la tica.

16. Teorías más
Importantes en la
Didáctica de la
Matemática

17. • Modelización y resolución de
problemas .
• Razonamiento matemático
• Lenguaje y comunicación
• Estructura interna
• Naturaleza relacional de las
matemáticas
• Exactitud y aproximación
• Transposición Didáctica
• Contrato Didáctico
• Obstáculos Epistemológicos
• Teoría de los Campos Conceptuales
• Situaciones Didáctica y A-didácticas
• Ingeniería Matemática

18. TICAS
En la reflexión sobre las propias concepciones hacia las
matemáticas habrán surgido
sobre las matemáticas, la actividad matemática y la
capacidad para aprender matemáticas. Pudiera parecer que
esta discusión muy alejada de los intereses prácticos del
profesor, interesado fundamentalmente por
(u
otro tema) a sus alumnos. La preocupación es un
cierto conocimiento, forma parte de la epistemología o
teoría del conocimiento, una de las ramas de la filosofía.

19. Entre la gran variedad de creencias sobre las relaciones entre las matemáticas y sus
aplicaciones y sobre el papel de éstas en la enseñanza y el aprendizaje, podemos
identificar dos concepciones extremas:
Una de estas concepciones, que fue n entre muchos ticos profesionales
hasta hace unos os, considera que el alumno debe adquirir primero las estructuras
fundamentales de las ticas de forma tica. Se supone que una vez
adquirida esta base, sera cil solo pueda resolver las aplicaciones
y problemas que se le presenten.
La tica pura y la aplicada an dos disciplinas distintas; y las estructuras
ticas abstractas deben preceder a sus aplicaciones en la Naturaleza y Sociedad.
Esta n de las ticas se designa como " - nica". Con esta
n es sencillo construir un culo, puesto que no hay que preocuparse por
las aplicaciones en otras reas. Estas aplicaciones se “ an”, abstrayendo los
conceptos, propiedades y teoremas ticos, para constituir un dominio
tico “puro”.

20. n constructivista
Otros ticos y profesores de ticas consideran que debe haber una
estrecha n entre las ticas y sus aplicaciones a lo largo de todo el
culo. Piensan que es importante mostrar a los alumnos la necesidad de cada
parte de las ticas antes de que les sea presentada. Los alumnos an
ser capaces de ver mo cada parte de las ticas satisfacen una cierta
necesidad.
La n de un culo de acuerdo con la n constructivista es
compleja, porque, s de conocimientos ticos, requiere conocimientos
sobre otros campos. Las estructuras de las ciencias sicas, gicas, sociales son
relativamente s complejas que las ticas y no siempre hay un isomorfismo
con las estructuras puramente ticas. Hay una abundancia de material
disperso sobre aplicaciones de las ticas en otras reas, pero la tarea de
n, ne n no es sencilla.

21. TICAS
Y
SOCIEDAD

22. Cuando tenemos en cuenta el tipo de ticas que queremos
ar y la forma de llevar a cabo esta anza debemos
reflexionar sobre dos fines importantes de esta anza:
 Que los alumnos lleguen a comprender y a apreciar el
papel de las ticas en la sociedad, incluyendo sus diferentes
campos de n y el modo en que las ticas han
contribuido a su desarrollo.
 Que los alumnos lleguen a comprender y a valorar el
todo tico, esto es, la clase de preguntas que un uso
inteligente de las ticas permite responder, las formas
sicas de razonamiento y del trabajo tico, asi como su
potencia y limitaciones.

23. TICAS?
RICAS

25. Las ticas constituyen el n sobre el que se construyen los modelos
ficos, toman parte en el proceso de n de la realidad, y en muchas
ocasiones han servido como medio de n de estos modelos. Por ejemplo, han
sido lculos ticos los que permitieron, mucho antes de que pudiesen ser
observados, el descubrimiento de la existencia de los ltimos planetas de nuestro
sistema solar.
Sin embargo, la n de las ticas no lo se ha producido por
n de conocimientos o de campos de n. Los propios conceptos
ticos han ido modificando su significado con el transcurso del tiempo,
ndolo, ndolo o ndolo, adquiriendo relevancia o, por el contrario,
siendo relegados a segundo plano.

27. TICA
Uno de los fines de la
n es formar
ciudadanos cultos, pero el
concepto de cultura es
cambiante y se a cada vez
s en la sociedad moderna.
Cada vez s se reconoce el
papel cultural de las
ticas y la n
tica n tiene
como fin proporcionar esta
cultura. El objetivo principal no
es convertir a los futuros
ciudadanos en “ ticos
aficionados”, tampoco se trata
de capacitarlos en lculos
complejos, puesto que los
ordenadores hoy a resuelven
este problema.

29. Lo que se pretende es proporcionar una cultura con varios componentes
interrelacionados:
a) Capacidad para interpretar y evaluar ticamente la n
tica y los argumentos apoyados en datos que las personas
pueden encontrar en diversos contextos, incluyendo los medios de
n, o en su trabajo profesional.
a) Capacidad para discutir o comunicar n
tica, cuando sea relevante, y competencia para resolver los
problemas ticos que encuentre en la vida diaria o en el
trabajo profesional.

30. N DE PROBLEMAS
El dar un papel primordial a la n de
problemas y a la actividad de n tiene
importantes repercusiones desde el punto de vista
educativo. a cuanto menos contradictorio con la
nesis rica de las ticas, al igual que con
sus aplicaciones actuales, presentar las ticas
a los alumnos como algo cerrado, completo y alejado
de la realidad. Debe tenerse en cuenta, por una
parte, que determinados conocimientos
ticos permiten modelizar y resolver
problemas de otros campos y por otra, que a
menudo estos problemas no estrictamente
ticos en su origen proporcionan la base
intuitiva sobre la que se elaboran nuevos
conocimientos ticos.

32. 1. En el siguiente problema, ¿ l es el conocimiento tico
significado intuitivo permite
construir sobre dicho conocimiento? Inventa otros problemas
sencillos que permitan construir un significado diferenciado para
el conocimiento en n.
Problema. Unos os llevan a clase caramelos. s lleva 5, a
8, Jose 6, Carmen 1 y Daniel no lleva ninguno. ¿ mo repartir los
caramelos de forma equitativa?
2. contenidos ticos an tiles para resolver los
siguientes tipos de problemas:
􏰀 Construir a escala la maqueta de un edificio
 Determinar en forma aproximada la altura de una torre, desde el
suelo.
 Calcular el mero de lentejas en un paquete de kilo, sin
contarlas todas.

33. Desde el punto de vista de la anza de las ticas, las
reflexiones anteriores deben concretarse a la edad y conocimientos de
los alumnos. No podemos proponer los mismos problemas a un
tico, a un adulto, a un adolescente o a un o, porque sus
necesidades son diferentes. Hay que tener claro que la realidad de los
alumnos incluye su propia n del entorno sico y social y
componentes imaginadas y dicas que despiertan su s en
mayor medida que pueden hacerlo las situaciones reales que
interesan al adulto.
En consecuencia, la n del conocimiento tico
mediante la n de problemas reales no se consigue
traspasando de forma nica situaciones "reales", aunque sean
muy pertinentes y significativas para el adulto, ya que stas pueden no
interesar a los alumnos.

34. TICO
RICO-INDUCTIVO
El proceso rico de n de las ticas nos muestra la
importancia del razonamiento rico-inductivo que, en muchos
casos, a un papel mucho s activo en la n de nuevos
conceptos que el razonamiento deductivo.
Esta n describe n la forma en que trabajan los
ticos, quienes no formulan un teorema “a la primera”. Los tanteos
previos, los ejemplos y contraejemplos, la n
sucede, etc., son las
nticas pistas para elaborar proposiciones y as. Esta fase intuitiva es la
que convence ntimamente al tico de que el proceso de n
del conocimiento va por buen camino. La n formal suele aparecer casi
siempre en una fase posterior.
Esta n se opone frontalmente a la tendencia, cilmente observable
en algunas propuestas curriculares, a relegar los procedimientos intuitivos a un
segundo plano, tendencia que priva a los alumnos del s poderoso
instrumento de ny n del conocimiento tico.

35. • Deducción: es una secuencia finita de fórmulas, de las
1 cuales la última es designada como la conclusión (la conclusión de la
deducción), y todas las fórmulas en la secuencia son, o bien
axiomas, o bien premisas, o bien inferencias directas a partir de
fórmulas previas en la secuencia por medio de reglas de inferencia.
• Inducción: un tipo de razonamiento en que la verdad de
2 las premisas brinda apoyo a la verdad de la conclusión, pero no
la garantiza.
• Empírico. Conocimiento basado en la
experiencia, experimentación e investigación, y en último
término, en la percepción, pues nos dice qué es lo que existe y
3 cuáles son sus características, pero no nos dice que algo deba
ser necesariamente así y no de otra forma; tampoco nos da
verdadera universalidad. Consiste en todo lo que se sabe y que
es repetido continuamente teniendo o sin tener un
conocimiento científico.

36. y construcción del conocimiento matemático.Los
no formulan un teorema “a la primera”. tanteos previos, los ejemplos y
contraejemplos, la solución de un caso particular, la posibilidad de modificar las
•condiciones iniciales y ver qué sucede, etc., son las auténticas pistas para elaborar y contar el
Al disponer puntos en el plano en forma cuadrangular
proposiciones y teorías. Esta fase intuitiva es la que convence íntimamente al
9. Al matemáticopuntosel proceso de construcción cuadrangular lospor buen camino. La
disponer de que en el plano en en cadaconocimientoyva cuadrados, obtenemos en
mero total de stos forma del uno de contar el número total de éstos los
cada unollamados suele meroscasi siempre en una 1,"números cuadrados": 1, 4, 9, 16, ...
deducción formal "
de los cuadrados, obtenemos los llamados 4, 9, 16, ...
aparecer cuadrados": fase posterior.
Esta constatación se opone frontalmente a la tendencia, fácilmente observable en
algunas propuestas curriculares,*a relegar los procedimientos intuitivos a un segundo
** ***
plano, tendencia que priva a los alumnos del más poderoso instrumento de exploración
**
y construcción del conocimiento matemático.
***
***
disponer
los primeros 10 y contar el número 9, de éstos
a) ¿ 9. Alunoas lospuntoslos elobtenemosformanúmeros cuadrados? 1, 4,total16, ... en
en plano en cuadrangular
a) ¿Podríasde escribir primeros los llamados "números cuadrados":
cada escribir
cuadrados, 10 meros cuadrados?
b) Llamaremos nCal al * cuadrado *cuya base está formada por n puntos ¿Puedes
b) Llamaremos C n número * * mero ** formada por n
encontrar una expresión general para Cn ?
puntos ¿Puedes encontrar una * * * n general para Cn ?
**
c) ¿Puedes dar algún tipo de razonamiento que la justifique?
c) ¿Puedes dar n tipo de razonamiento que la justifique?
***
a) ¿Podrías escribir los primeros 10 números cuadrados?
10. Repite el proceso para Cn al"números triangulares": formada por n puntos ¿Puedes
b) Llamaremos los número cuadrado cuya base está
encontrar una expresión general para Cn ?
c) ¿Puedes dar algún tipo * razonamiento que la justifique?
de * * *
• Repite el proceso para los " meros triangulares":
** **
10. Repite el proceso para los "números triangulares": **
* * * *** * ***
** ** **
*** ***
****
****
11. Analiza el papel del razonamiento empírico-inductivo y deductivo en la resolución de
los problemas anteriores del razonamiento empírico-inductivo y deductivo en la resolución de
11. Analiza el papel
los problemas anteriores
Analiza el papel del razonamiento rico-inductivo y deductivo en la
n de los problemas anteriores

37. N
Desde una perspectiva gica -y n gica-, es
importante diferenciar el proceso de n del conocimiento
tico de las sticas de dicho conocimiento en un estado
avanzado de n. La n, n y ausencia de
ambigüedad del conocimiento tico debe ser la fase final de un
largo proceso de n a la realidad, de n de
instrumentos intelectuales eficaces para conocerla, analizarla y
transformarla.
Ciertamente, como ciencia constituida, las ticas se caracterizan por
su n, por su cter formal y abstracto, por su naturaleza deductiva
y por su n a menudo tica. Sin embargo, tanto en la
nesis rica como en su n individual por los alumnos, la
n del conocimiento tico es inseparable de la actividad
concreta sobre los objetos, de la n y de las aproximaciones
inductivas activadas por la n de tareas y la n de
problemas particulares. La experiencia y n de las
nociones, propiedades y relaciones ticas a partir de la actividad
real es, al mismo tiempo, un paso previo a la n y una n
necesaria para interpretar y utilizar correctamente todas las posibilidades
que encierra dicha n.

38. Las , como el resto de las disciplinas ficas, aglutinan un
conjunto de conocimientos con unas sticas propias y una
determinada estructura y n internas. Lo que confiere un
cter distintivo al conocimiento tico es su enorme poder
como instrumento de n, conciso y sin ambigüedades. Gracias
a la amplia n de diferentes sistemas de n lica
( meros, letras, tablas, ficos, etc,), las ticas son tiles para
representar de forma precisa informaciones de naturaleza muy
diversa, poniendo de relieve algunos aspectos y relaciones no
directamente observables y permitiendo anticipar y predecir hechos
situaciones o resultados que a no se han producido.

39. Ejemplo:
Un mero par se puede escribir como 2n. Esta n es equivalente
a (n+1)+(n-1). Pero esta ltima n nos da una nueva n
ya que muestra que todo mero par es la suma de dos impares
consecutivos.
a sin embargo neo, o al menos superficial, suponer que esta
capacidad del conocimiento tico para representar, explicar y
predecir hechos, situaciones y resultados es simplemente una
consecuencia de la n de notaciones licas precisas e
vocas en cuanto a las informaciones que permiten representar. En
realidad, si las notaciones licas pueden llegar a ar
efectivamente estos papeles es debido a la propia naturaleza del
conocimiento tico en su base y al que sirven de soporte.

40. Identifica los diferentes medios de n en los textos con que se
trabaja en el aula( rminos, mbolos, ficas, diagramas). Da ejemplos
de los conceptos citos y citos a que hacen referencias. ¿ mo
se representan los diferentes conceptos?
¿ mo podemos comunicar las ticas a alumnos con
discapacidad, como ceguera, disminución motriz, etc.? ¿Piensas que
pueden tener dificultades especiales con alguna parte de las
ticas debido a su carencia?

41. ESTRUCTURA INTERNA
La insistencia sobre la actividad constructiva no supone en n caso
ignorar que, como cualquier otra disciplina fica, las ticas
tienen una estructura interna que relaciona y organiza sus diferentes
partes. s n, en el caso de las ticas esta estructura es
especialmente rica y significativa.
Hay una componente vertical en esta estructura, la que fundamenta unos
conceptos en otros, que impone una determinada secuencia temporal en
el aprendizaje y que obliga, en ocasiones, a trabajar algunos aspectos con
la nica finalidad de poder integrar otros que son los que se consideran
verdaderamente importantes desde un punto de vista educativo.

42. LA MATEMATIZACIÓN HORIZONTAL
Nos lleva del mundo real al mundo de los símbolos y posibilita tratar
matemáticamente un conjunto de problemas. En esta actividad son
característicos los siguientes procesos:
• IDENTIFICAR las matemáticas en contextos generales
• ESQUEMATIZAR
• FORMULAR y VISUALIZAR un problema de varias maneras
• DESCUBRIR relaciones y regularidades
• RECONOCER aspectos isomorfos en diferentes problemas
• TRANSFERIR un problema real a uno matemático
• TRANSFERIR un problema real a un modelo matemático conocido.

43. LA MATEMATIZACIÓN VERTICAL
Consiste en el tratamiento específicamente matemático de las
situaciones, y en tal actividad son característicos los siguientes
procesos:
• REPRESENTAR una relación mediante una fórmula
• UTILIZAR diferentes modelos
• REFINAR y AJUSTAR modelos
• COMBINAR e INTEGRAR modelos
• PROBAR regularidades
• FORMULAR un concepto matemático nuevo
• GENERALIZAR
¿ Con qué acciones reales, hacemos esto en el aula?

44. Sin embargo, interesa destacar una vez s que casi nunca existe un camino
nico, ni tan siquiera uno claramente mejor, y si lo hay tiene una
n s de tipo gico que gico. Por el
contrario, determinadas concepciones sobre la estructura interna de las
ticas pueden llegar incluso a ser funestas para el aprendizaje de las
mismas, como ha puesto claramente de relieve el intento de fundamentar
toda la tica escolar en la a de conjuntos.
Considera los siguientes conjuntos ricos: meros
racionales, meros naturales, meros enteros, meros
decimales, meros primos. ¿ mo ?
¿ en los os curriculares, se contempla una
anza clica de algunos conceptos? Identifica algunos
conceptos que aparezcan clicamente en los diferentes
niveles de la n primaria.

45. NATURALEZA RELACIONAL
El conocimiento - tico hunde sus ces en la
capacidad del ser humano para establecer relaciones entre
los objetos o situaciones a partir de la actividad que ejerce
sobre los mismos y, muy especialmente, en su capacidad
para abstraer y tomar en n dichas relaciones en
detrimento de otras igualmente presentes.

46. ,

47. Ejemplo
En las frases “A es s grande que B”, "A mide tres metros s que B”,
“B mide tres metros
mismos, sino la n existente entre una
propiedad -el o- que comparten ambos objetos y que precisamente es
el resultado de la actividad de compararlos en lo que concierne a esta
propiedad en detrimento de otras muchas posibles (color forma, masa,
densidad volumen, etc.).
Las relaciones s grande que, s o que, tres metros s que,
tres metros menos que, etc. son pues verdaderas construcciones
mentales y no una simple lectura de las propiedades de los objetos. Incluso la
referencia a los objetos A y B como grande y o supone una actividad
de n con elementos s difusos, como pueden ser objetos
similares con los que se ha tenido alguna experiencia anterior.

48. punto el conocimiento tico
implica la n de relaciones elaboradas a partir de la actividad sobre
los objetos. Las ticas son pues s constructivas que deductivas,
desde la perspectiva de su n y n. Si desligamos el
conocimiento tico en su origen,
corremos el peligro de caer en puro formalismo. Perderemos toda su
potencialidad como instrumento de n, ny n.
Otra n curricular de la naturaleza relacional de las ticas es la
existencia de estrategias o procedimientos generales que pueden utilizarse en
campos distintos y con sitos diferentes.

49. Ejemplo
Numerar, contar, ordenar, clasificar, simbolizar, inferir, etc.
son herramientas igualmente tiles en a y en
stica.
Para que los alumnos puedan percibir esta similitud de
estrategias y procedimientos y su utilidad desde pticas
distintas, es necesario dedicarles una n especial
seleccionando cuidadosamente los contenidos de la
anza.

50. N
Una stica adicional de las ticas, que ha ido
ndose cada vez s patente a lo largo de su desarrollo
rico, es la dualidad desde la que permite contemplar la
realidad. Por un lado la tica es una “ciencia exacta”, los
resultados de una n, una n son vocos.
Por otro, al comparar la n tica de un cierto
hecho de la realidad, siempre es aproximada, porque el modelo
nunca es exacto a la realidad. Si bien algunos aspectos de esta
dualidad aparecen ya en las primeras experiencias ticas
de los alumnos, otros lo hacen s tarde.

51. Es frecuente que las propuestas curriculares potencien
exclusivamente una cara de la moneda: la que se ajusta
mejor a la imagen tradicional de las ticas como
ciencia exacta. Asi, por ejemplo, se prefiere la tica
” o “no”, “verdadero” o “falso”) a la de la
probabilidad (“es posible que. . . “, “con un nivel de
n de. . . “); la de la exactitud (“la diagonal mide
√2”, “el rea de un rculo es πr2”,...) a la de la n
(“me equivoco como mucho en una cima”, “la n
urea es aproximadamente 5/3”, ...).
Las ticas escolares deben potenciar estos dobles
enfoques, y ello no lo por la riqueza nseca que
encierran, sino porque los que han sido relegados hasta
ahora a un segundo plano tienen una especial incidencia en
las aplicaciones actuales de las ticas.

52. ¿Es posible medir con exactitud la longitud de una costa? ¿la
cantidad de agua embalsada en un pantano? ¿el nivel de
ruido ambiental? Pon otros ejemplos en que la medida lo
s tiene en estos casos un
valor aproximado de la medida?

53. TICOS:
CONCEPTOS, PROCED
IMIENTOS Y
ACTITUDES

54. En el Curriculum académico se entiende por contenido
escolar tanto los que habitualmente se han considerado
contenidos, los de tipo conceptual, como otros que han
estado s ausentes de los planes de estudio y que no
por ello son menos importantes: contenidos relativos a
procedimientos, y a normas, valores y actitudes. En la
escuela los alumnos aprenden de hecho estos tres tipos
de contenidos. Todo contenido que se aprende es
n susceptible de ser ado, y se considera tan
necesario planificar la n con respecto a los
contenidos de tipo conceptual como planificarla con
n a los otros tipos de contenido.

55. En el Curriculum se encuentran tres apartados distintos los
tres tipos de contenido. El primero de ellos es el que
presenta los conceptos, hechos y principios. Los hechos y
conceptos han estado siempre presentes en los programas
escolares, no tanto los principios. Por principios se
entiende enunciados que describen mo los cambios que
se producen en un objeto o n se relacionan con los
cambios que se producen en otro objeto o n.

56. El segundo tipo de contenido es el que se refiere a los procedimientos.
Un procedimiento es un conjunto de acciones ordenadas, orientadas a la
n de una meta. Se puede hablar de procedimientos mas o
menos generales en n del mero de acciones o pasos implicados
en su n, de la estabilidad en el orden de estos pasos y del tipo
de meta al que van dirigidos. En los contenidos de procedimientos se
indican contenidos que n caben bajo la n de
"destrezas’’, cnicas’’ o “estrategias’’, ya que todos estos rminos
aluden a las sticas aladas como definitorias de un
procedimiento. Sin embargo, pueden diferenciarse en algunos casos en
este apartado contenidos que se refieren a procedimientos o destrezas
s generales que exigen para su aprendizaje otras cnicas s
ficas, relacionadas con contenidos concretos.
APLICACIÓN:
1. La suma de meros naturales es a la vez un concepto (concepto de suma) y un
procedimiento (sumar). Explica mo el aprendizaje del
procedimiento y del concepto en este caso particular.
2. Formula dos objetivos conceptuales y dos procedimentales referentes a la suma de
meros naturales.

57. El ltimo apartado, que aparece en todos los bloques de contenido, es el que
se refiere a los valores, normas y actitudes. La pertinencia o no de incluir este
tipo de contenido en el d o curricular puede suscitar alguna duda. Hay
personas que consideran que puede ser peligroso estipular unos valores y
unas normas y actitudes para todos los alumnos. Desde esta propuesta
curricular se pretende, en cambio, que los profesores programen y trabajen
estos contenidos tanto como los s ya que, de hecho, los alumnos
aprenden valores, normas y actitudes en la escuela. La nica diferencia, que
se considera en esta propuesta una ventaja, es que ese aprendizaje no se
producira de una manera no planificada, formando parte del culo
oculto, sino que la escuela intervendra intencionalmente favoreciendo las
situaciones de anza que aseguraran el desarrollo de los valores, normas
y actitudes que, a partir de las cuatro fuentes del culo, pero
especialmente de la fuente gica, se consideren oportunas.
PARA ANALIZAR: ¿ mo crees que se forman las actitudes
negativas hacia las ticas? ¿ mo se ponen de manifiesto?
Entrega al menos dos ejemplos donde tú has presentado una
actitud positiva y una actitud negativa frente al aula.

58. PARA RECORDAR:
La entre contenidos
, y es, en
primer lugar y sobre todo, de naturaleza gica. Es
decir, llama la n sobre la conveniencia de adoptar un
enfoque determinado en la manera de trabajar los contenidos
seleccionados. Esta es la n por la cual, en ocasiones, un mismo
contenido aparece repetido en las tres as: la n en
este caso traduce la idea gica de que el contenido en
n debe ser abordado convergentemente desde una
perspectiva conceptual, procedimental y actitudinal. En otras
ocasiones, sin embargo, un determinado contenido aparece
nicamente en una u otra de las tres as, con ello se
sugiere que dicho contenido, por su naturaleza y por la n
educativa propia de la etapa, debe ser abordado con un enfoque
prioritariamente conceptual, procedimental o actitudinal.

59. punto el conocimiento
tico implica la n de relaciones elaboradas a
partir de la actividad sobre los objetos. Las ticas son
pues s constructivas que deductivas, desde la perspectiva de
su n y n. Si desligamos el conocimiento
tico en su
origen, corremos el peligro de caer en puro formalismo.
Perderemos toda su potencialidad como instrumento de
n, ny n.
Otra n curricular de la naturaleza relacional de las
ticas es la existencia de estrategias o procedimientos
generales que pueden utilizarse en campos distintos y con
sitos diferentes.

61. BIBLIOGRAFÍA
• Matematicas y su Didactica para Maestros
www.ugr.es/~jgodino/edumat-maestros/welcome.htm
• La Didáctica de las Matemáticas (NTI, RTEE)
www.gobiernodecanarias.org/educacion/rtee/didmat.htm
• Didáctica de la Matemática
Nora Cabanne, 2007, Editoria Bonum
• Didactica De La Matematica En La Educacion Primaria Intercultural
Cristina Jurado, 1993, Series Pedagógicas didácticas
• Didáctica de Las Matemáticas: Cuestiones, Teoría y Práctica en el Aula
Antony Orton, 1996, Ediciones Morata, ministerio de Educacion de
España. Cuarta edición