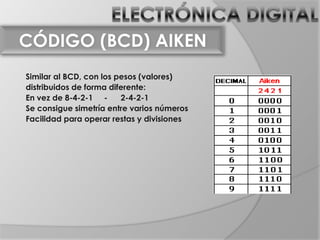
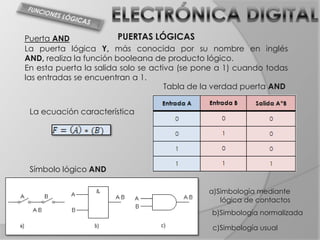
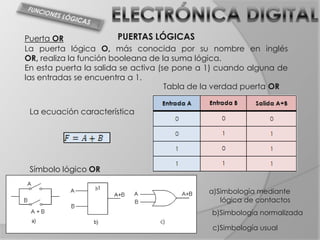
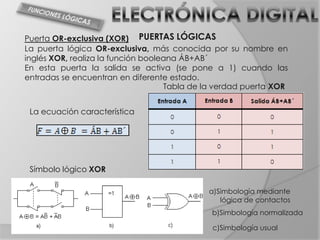
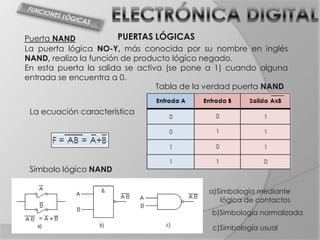
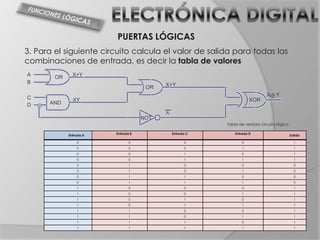
El documento trata sobre el álgebra de Boole y puertas lógicas. Introduce el álgebra de Boole, incluyendo sus operaciones básicas, postulados y teoremas. Luego explica las funciones lógicas, tablas de verdad y diferentes tipos de puertas lógicas como AND, OR, NOT, NAND y NOR. Finalmente incluye ejemplos de circuitos lógicos y tablas de verdad.

1. ALGEBRA DE BOOLE
FUNCIONES LÓGICAS
SIMPLIFICACIÓN DE FUNCIONES LÓGICAS
SIMPLIFICACIÓN MEDIANTE MAPAS DE KARNAUGH
Víctor Martín Ruiz
Roberto Maté Barbero
Jaime Pérez Sáinz
Iván Vallejo Porras

2. Víctor Martín Ruiz
Roberto Maté Barbero
Jaime Pérez Sáinz
Iván Vallejo Porras

3. CÓDIGO BCD
Decimal Codificado en Binario.
Es una manera de representar número
decimales en binario.

4. CÓDIGO (BCD) AIKEN
Similar al BCD, con los pesos (valores)
distribuidos de forma diferente:
En vez de 8-4-2-1 - 2-4-2-1
Se consigue simetría entre varios números
Facilidad para operar restas y divisiones

5. CÓDIGO BCD EXCESO3
No ponderado, no hay pesos
Se obtiene sumando 3 al código BCD natural
Se obtienen códigos simétricos
Facilidad de operar restas y divisiones

6. CÓDIGO GRAY
No ponderado, no hay pesos
Solo existe diferencia de un digito entre
un término y el siguiente.
“Código progresivo”

7. CÓDIGO GRAY
BINARIO A GRAY
1. Se suma el número en binario con el mismo, pero el
segundo sumando debe correrse una cifra a la derecha. Ver el
gráfico.
2. Se realiza una suma binaria cifra con cifra sin tomar en
cuenta el acarreo y se obtiene la suma total.
3. Al resultado anterior se le elimina la ultima cifra del lado
derecho (se elimina el cero que está en rojo), para obtener el
código GRAY.

8. CÓDIGO GRAY
GRAY A BINARIO
1. El primer dígito del código Gray será el mismo que el del
binario
2. Si el segundo dígito del código Gray es "0", el segundo
dígito binario es igual al primer digito binario, si este dígito
es "1" el segundo dígito binario es el inverso del primer dígito
binario.
3. Si el tercer dígito del código Gray es "0", el tercer dígito
binario es igual al segundo dígito binario, si este dígito es
"1", el tercer dígito binario es el inverso del segundo dígito
binario..... y así hasta terminar.
0 - IGUAL
1 - DISTINTO

9. Víctor Martín Ruiz
Roberto Maté Barbero
Jaime Pérez Sáinz
Iván Vallejo Porras

10. INTRODUCCIÓN
El Álgebra de Boole, fue presentada originalmente por el
inglés George Boole, en el año de 1854 en su artículo
"An Investigation of the Laws of Thoght ... ", sin
embargo, las primeras aplicaciones a circuitos de
conmutación fueron desarrolladas por Claude
Shannon en su tesis doctoral "Análisis simbólico de
los circuitos de conmutación y relés" en 1938.

11. La herramienta fundamental para el análisis y diseño de
circuitos digitales es el Álgebra Booleana.
Esta álgebra es un conjunto de reglas matemáticas
(similares en algunos aspectos al álgebra
convencional), pero que tienen la virtud de corresponder
al comportamiento de circuitos basados en dispositivos
de conmutación
(interruptores, relevadores, transistores, etc).
En este capítulo se presentan las operaciones básicas y
los postulados que definen el álgebra booleana

12. Las operaciones en el Algebra de Boole
En el Álgebra de Boole hay dos peraciones, denotadas con los
símbolos + y .
El + y el . del Algebra de Boole se aplican a bits, es decir, a
números que sólo pueden ser el '0' ó el '1'

13. La operación + La operación . La operación ´

14. POSTULADOS DEL ÁLGEBRA BOOLEANA

15. POSTULADOS DEL ÁLGEBRA
BOOLEANA
POSTULADO 1
El álgebra booleana es un sistema algebraico definido en un conjunto
B, el cual contiene dos o más elementos y entre los cuales se definen
dos operaciones denominadas "suma u operación OR" ( + ) y
"producto o multiplicación u operación AND" (.) que cumplen las
siguientes propiedades:

16. POSTULADO 2
Existencia de Neutros. Existen en B el elemento neutro de la
suma, denominado 0 y el neutro de la multiplicación, denominado
1, tales que para cualquier elemento x de s:
(a) x+0=x
(b) x. 1 = x

17. POSTULADO 3
Conmutatividad. Para cada x, y:
(a) x+y = y+x (b) x y =y x

18. POSTULADO 4
Asociatividad. Para cada x, y, z en B:
(a) x + (y + z) = (x + y) + z
(b) x (y z) = (x y) z

19. POSTULADO 5
Distributividad. Para cada x, y, z en B:
(a) x+(y z)=(x+y) (x+z)
(b) x (y+z)=(x y)+(x z)

20. POSTULADO 6
Existencia de Complementos. Para cada x en B existe un
elemento único denotado x (también denotado x’), llamado
complemento de x tal que
(a) x + x´ = 1
(b) x x´ = 0

21. TEOREMAS DEL ÁLGEBRA DE BOOLE

22. TEOREMAS DEL ÁLGEBRA DE BOOLE

23. Víctor Martín Ruiz
Roberto Maté Barbero
Jaime Pérez Sáinz
Iván Vallejo Porras

24. INTRODUCCIÓN:
La electrónica digital y, por tanto, los circuitos digitales se emplean
en todo tipo de sistemas de control industrial, procesos de datos, y
otros muchos equipos como pueden ser los dispositivos de
seguridad, equipos de
navegación, electrodomésticos, telefonía, etc.
Estos circuitos requieren para su construcción una serie de
elementos que materialicen los principios del álgebra de
Boole, base matemática de la electrónica digital. Esta realización
física la constituyen las denominadas puertas lógicas.
Adición, unión o función OR
¿qué es una función lógica? f(A,B)=A+B
“Es todo conjunto de variables Producto, intersección o
relacionadas entre sí por función AND
cualquiera de las tres operaciones f(A,B)= A*B
básicas del álgebra de Boole. Complementación, inversión o
f=f(A,B,C...)” función NOT
f(A)= Á, A

25. Tabla de la verdad
Es una forma de representación, en la que se calcula el valor que
toma la función para cada una de las combinaciones de sus
variables.

26. Puertas lógicas
Las puertas lógicas son los componentes electrónicos, presentados
en forma de circuito integrado, mediante los cuales pueden
realizarse las funciones lógicas elementales.
Cada puerta lógica consiste en una red de dispositivos
interruptores que cumple las condiciones booleanas para el
operador particular. Son esencialmente circuitos de conmutación
integrados en un chip.
En nanotecnología se está desarrollando el uso de una compuerta
lógica molecular, que haga posible la miniaturización de circuitos.
Expresión matemática
3 formas de definir Símbolo lógico
una función lógica
Tabla de la verdad

27. PUERTAS LÓGICAS
Puerta SÍ o BUFFER
La puerta lógica SÍ, realiza la función booleana igualdad. En la
práctica se suele utilizar como amplificador de corriente o como
seguidor de tensión, para adaptar impedancias (buffer en inglés)
La ecuación característica Tabla de la verdad puerta SÍ
Símbolo lógico SÍ
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

28. Puerta AND PUERTAS LÓGICAS
La puerta lógica Y, más conocida por su nombre en inglés
AND, realiza la función booleana de producto lógico.
En esta puerta la salida solo se activa (se pone a 1) cuando todas
las entradas se encuentran a 1.
Tabla de la verdad puerta AND
La ecuación característica
Símbolo lógico AND
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

29. Puerta OR PUERTAS LÓGICAS
La puerta lógica O, más conocida por su nombre en inglés
OR, realiza la función booleana de la suma lógica.
En esta puerta la salida se activa (se pone a 1) cuando alguna de
las entradas se encuentra a 1.
Tabla de la verdad puerta OR
La ecuación característica
Símbolo lógico OR
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

30. Puerta OR-exclusiva (XOR) PUERTAS LÓGICAS
La puerta lógica OR-exclusiva, más conocida por su nombre en
inglés XOR, realiza la función booleana ÁB+AB´
En esta puerta la salida se activa (se pone a 1) cuando las
entradas se encuentran en diferente estado.
Tabla de la verdad puerta XOR
La ecuación característica
Símbolo lógico XOR
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

31. Puerta NOT PUERTAS LÓGICAS
La puerta lógica NO, más conocida por su nombre en inglés
NOT, realiza la función booleana de inversión o negación de una
variable.
La salida siempre toma el estado contrario a la entrada
Tabla de la verdad puerta NOT
La ecuación característica
Símbolo lógico NOT
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

32. Puerta NAND PUERTAS LÓGICAS
La puerta lógica NO-Y, más conocida por su nombre en inglés
NAND, realiza la función de producto lógico negado.
En esta puerta la salida se activa (se pone a 1) cuando alguna
entrada se encuentra a 0.
Tabla de la verdad puerta NAND
La ecuación característica
Símbolo lógico NAND
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

33. Puerta NOR PUERTAS LÓGICAS
La puerta lógica NO-O, más conocida por su nombre en inglés
NOR, realiza la función de suma lógica negada.
En esta puerta la salida se activa (se pone a 1) cuando no tiene
ninguna entrada activada
Tabla de la verdad puerta NOR
La ecuación característica
Símbolo lógico NOR
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

34. Puerta XNOR PUERTAS LÓGICAS
La puerta lógica equivalente, realiza la función booleana AB+ÁB´
En esta puerta la salida se activa (se pone a 1) solo si las dos
entradas son iguales (2 encendidos o 2 apagados)
Tabla de la verdad puerta XNOR
La ecuación característica
Símbolo lógico XNOR
a)Simbología mediante
lógica de contactos
b)Simbología normalizada
c)Simbología usual

35. EJERCICIOS PUERTAS LÓGICAS
1. Dibujar los correspondientes circuitos de las siguientes funciones
lógicas X X X X
SÍ NOT
a) F(A,B,C)= (A*B+C*D)*C
A X X
XY XY
AND NAND
B Y Y
F
C X X
X+Y X+Y
D OR NOR
Y Y
X X
a) F(A,B,C)= (A*B+C*D)*(A*B+C´) XOR
X+Y
XNOR
X+Y
X X X X
Y SÍ Y NOT
A
X X
B XY XY
AND NAND
Y Y
C
D X X+Y X X+Y
OR NOR
Y Y
X X+Y X X+Y
XOR XNOR
Y Y

36. EJERCICIOS PUERTAS LÓGICAS
2. Dado un circuito formula la correspondiente función lógica
a)
A A (AB)
A (A (AB))x(AB x (C+D))
AB
B
AB x(C+D) F
C
C+D
D
(AB x (C+D)) + ((CD) x D )
D (C+D)x D
F (A,B,C,D)= A (A+B) x (AB)x(C+D) x (AB)x(C+D) + (C+D) x D

37. PUERTAS LÓGICAS
3. Para el siguiente circuito calcula el valor de salida para todas las
combinaciones de entrada, es decir la tabla de valores
A OR X+Y
B X+Y
OR
X+Y
C XY XOR
D AND
X
NOT
Tabla de verdad circuito lógico
Entrada A Entrada B Entrada C Entrada D Salida
0 0 0 0 1
0 0 0 1 1
0 0 1 0 1
0 0 1 1 1
0 1 0 0 0
0 1 0 1 0
0 1 1 0 0
0 1 1 1 0
1 0 0 0 1
1 0 0 1 1
1 0 1 0 1
1 0 1 1 1
1 1 0 0 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1

38. CONTINUARÁ
GRACIAS POR SU ATENCIÓN
Víctor Martín Ruiz
Roberto Maté Barbero
Jaime Pérez Sáinz
Iván Vallejo Porras