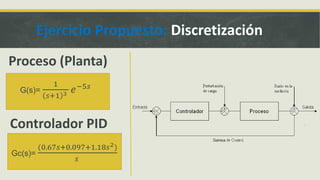
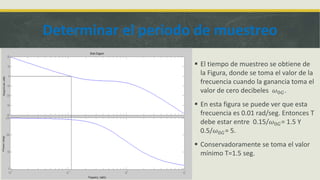
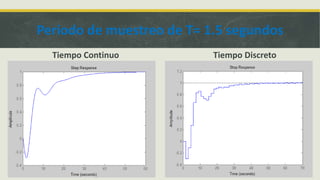
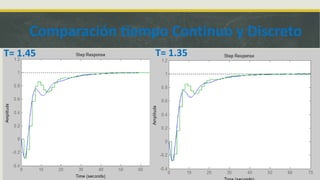
El documento detalla el diseño de un controlador PID utilizando el lugar geométrico de las raíces, incluyendo cálculos específicos de ganancias y tiempos de muestreo. Se establece un periodo de muestreo mínimo de 1.5 segundos y se discute la importancia de mantener un tiempo de muestreo cercano a cero para que la respuesta del sistema en tiempo discreto asemeje al continuo. El ejercicio también fomenta el aprendizaje de comandos en MATLAB y la resolución de un controlador PID.

1. Respuesta en tiempo
discreto de un
controlador PID
Profesor: Dr. José Ruben Lagunas Jimenez
Alumno: Daniel Alejandro Martinez Huicab

2. Diseñando el controlador a partir de
Lugar Geométrico de las Raíces
La Figura 1 muestra el lugar geométrico de las raíces del siguiente
proceso (planta):
Después de haber obtenido el LGR de un PID para el proceso
anterior obtuvimos una Ku= 1.13 como se muestra en la Figura 1 y
un 𝑻𝒖 =
2𝜋
𝑓
=
2𝜋
0.45
= 13.96
Por Zigler-Nichols, obtenemos que:
Figura 1. LGR en respuesta (PID)
G(s)=
1
(𝑠+1)^3
𝑒−5𝑠
Kp = 0.6 (Ku) = 0.678
Ki = Kp/Ti = 0.0971
Kd = (Kp)(Td) = 1.183
Ti = Tu/2 = 6.98
Td = Tu/8 = 1.745

3. Ejercicio Propuesto: Discretización
G(s)=
1
𝑠+1 3 𝑒−5𝑠
Gc(s)=
𝑠
Proceso (Planta)
Controlador PID
Gc(s)=
(0.67𝑠+0.097+1.18𝑠2)
𝑠

4. Determinar el periodo de muestreo
 El tiempo de muestreo se obtiene de
la Figura, donde se toma el valor de la
frecuencia cuando la ganancia toma el
valor de cero decibeles 𝜔0𝐺.
 En esta figura se puede ver que esta
frecuencia es 0.01 rad/seg. Entonces T
debe estar entre 0.15/𝜔0𝐺= 1.5 Y
0.5/𝜔0𝐺= 5.
 Conservadoramente se toma el valor
mínimo T=1.5 seg.

5. Periodo de muestreo de T= 1.5 segundos
Tiempo Continuo Tiempo Discreto

6. Comparación tiempo Continuo y Discreto
T= 1.45 T= 1.35

7. Retroalimentación
 El valor mínimo que puede hacer el muestreo para este caso es de 1.35 pues que al
intentar hacerlo con cualquier numero menor que 1.35 no permitía el muestreo, la
conclusión a la que se llego fue que entre mas cerca estuviera el tiempo T de 0 (cabe
recalcar que para este sistema no podría llegar menos de 1.35) este mismo tendía a
parecerse en la respuesta en frecuencia para el sistema en tiempo continuo.
 Con ello también concluyo que el ejercicio cumplió su objetivo, puesto que permitió
aprender comandos nuevos en MATLAB, además de la resolución de un controlador PID.