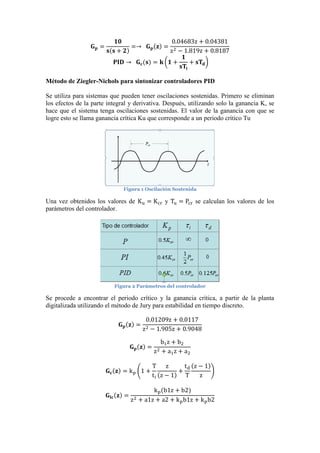
Este documento describe el proceso de sintonización de un controlador PID para un sistema de control digital usando el método de Ziegler-Nichols. Primero se determinan la ganancia crítica y el periodo crítico del sistema usando el método de Jury para estabilidad en tiempo discreto. Luego, usando estos valores y la tabla de Ziegler-Nichols, se calculan los parámetros del controlador PID. Finalmente, se simula el sistema controlado en Simulink para verificar su funcionamiento.

1. UNIVERSIDAD DE LAS FUERZAS ARMADAS-ESPE
DEPARTAMENTO DE ELÉCTRICA Y
ELECTRÓNICA
INGENIERÍA ELECTRÓNICA EN
AUTOMATIZACIÓN Y CONTROL
CONTROL DIGITAL
TEMA: SINTONIZACION DE CONTROLADOR
PID POR EL METODO DE LA ULTIMA
GANANCIA
NOMBRE:
ESPARZA ALEX
RODRÍGUEZ DIEGO
2014-06-19
Sintonizar el controlador PID por el método de la última ganancia

2. 𝐆 𝐩 =
𝟏𝟎
𝐬(𝐬 + 𝟐)
=→ 𝐆 𝐩(𝐳) =
0.04683z + 0.04381
z2 − 1.819z + 0.8187
𝐏𝐈𝐃 → 𝐆 𝐜(𝐬) = 𝐤 (𝟏 +
𝟏
𝐬𝐓𝐢
+ 𝐬𝐓𝐝)
Método de Ziegler-Nichols para sintonizar controladores PID
Se utiliza para sistemas que pueden tener oscilaciones sostenidas. Primero se eliminan
los efectos de la parte integral y derivativa. Después, utilizando solo la ganancia K, se
hace que el sistema tenga oscilaciones sostenidas. El valor de la ganancia con que se
logre esto se llama ganancia crítica Ku que corresponde a un periodo crítico Tu
Figura 1 Oscilación Sostenida
Una vez obtenidos los valores de Ku = Kcr y Tu = Pcr se calculan los valores de los
parámetros del controlador.
Figura 2 Parámetros del controlador
Se procede a encontrar el periodo crítico y la ganancia crítica, a partir de la planta
digitalizada utilizando el método de Jury para estabilidad en tiempo discreto.
𝐆 𝐩(𝐳) =
0.01209z + 0.0117
z2 − 1.905z + 0.9048
𝐆 𝐩(𝐳) =
b1z + b2
z2 + a1z + a2
𝐆 𝐜(𝐳) = kp (1 +
T
ti
z
(z − 1)
+
td
T
(z − 1)
z
)
𝐆𝐥𝐜(𝐳) =
kp(b1z + b2)
z2 + a1z + a2 + kpb1z + kpb2

3. Polinomio característico:
∆(z) = z2
+ a1z + a2 + kp b1z + kp b2
∆(z) = z2
+ (a1 + kp b1)z + a2 + kp b2
∆(𝐳) = 𝐳 𝟐
+ 𝐜 𝟏 𝐳 + 𝐜 𝟐
Test de Jury:
i) ∆(1)>0
∆(1) = 1 + 𝑎1 + 𝑘 𝑝 𝑏1 + 𝑎2 + 𝑘 𝑝 𝑏2 > 0
𝑘 𝑝 > −
1 + 𝑎1 + 𝑎2
𝑏1 + 𝑏2
ii) (-1)n∆(-1)>0
1 − 𝑎1 − 𝑘 𝑝 𝑏1 + 𝑎2 + 𝑘 𝑝 𝑏2 > 0
𝑘 𝑝 >
𝑎1 − 𝑎2 − 1
𝑏2 − 𝑏1
iii) |a0|<an
𝑎2 + 𝑘 𝑝 𝑏2 < 1
𝑘 𝑝 <
1 − 𝑎2
𝑏2
El intervalo a analizar es:
−
1 + 𝑎1 + 𝑎2
𝑏1 + 𝑏2
< 𝑘 𝑝 <
1 − 𝑎2
𝑏2
𝒌 𝒑 <
𝟏−𝒂 𝟐
𝒃 𝟐
 K crítico
Kcr =
𝟏 − 𝟎. 𝟗𝟎𝟒𝟖
𝟎. 𝟎𝟏𝟏𝟕
= 𝟖. 𝟏𝟑
𝛼 = −
𝑐1
2
=
𝑎1 + 𝐾𝑐𝑟 𝑏1
2
= −
−1.905 + 8.13 ∗ 0.01209
2
= 0.9033
𝜔 𝑜 =
1
𝑇
𝑐𝑜𝑠−1
𝛼
𝜔 𝑜 =
1
0.05
𝑐𝑜𝑠−1(0.9033) = 8.8679
𝑃𝑐𝑟 =
2𝜋
𝜔 𝑜
=
2𝜋
8.8679
= 0.7085
𝑷 𝒄𝒓 = 𝟎. 𝟕𝟎𝟖𝟓
Aplicando la tabla para un PID tenemos lo siguiente

4. 𝑘 𝑝 = 0.6𝐾𝑐𝑟 = 0.6(8.13)
𝒌 𝒑 = 𝟒. 𝟖𝟕𝟖
Ti =
Pcr
2
=
0.7085
2
𝑻𝒊 = 𝟎. 𝟑𝟓𝟒𝟐
𝑇𝑑 =
𝑃𝑐𝑟
8
=
0.7085
8
𝑻 𝒅 = 𝟎. 𝟎𝟖𝟖𝟓
Controlador PID:
𝐏𝐈𝐃 → 𝐆 𝐜(𝐬) = (𝟒. 𝟖𝟕𝟖) (𝟏 +
𝟏
𝐬(𝟎. 𝟑𝟓𝟒𝟐)
+ 𝐬(𝟎. 𝟎𝟖𝟖𝟓))
Digitalizando el controlador por Rectangular:
s =
z − 1
Tz
𝐆 𝐜(𝐬) = 𝐤 𝐩 (𝟏 +
𝟏
𝐬𝐓𝐢
+ 𝐬𝐓𝐝)
Gc(z) = kp (1 +
1
Ti
T z
z − 1
+ Td
z − 1
T z
)
𝐆 𝐜(𝐳) = 𝐤 𝐩 +
𝐤 𝐩 ∙ 𝐓
𝐓𝐢
∙
𝐳
𝐳 − 𝟏
+
𝐤 𝐩 ∙ 𝐓𝐝
𝐓
∙
𝐳 − 𝟏
𝐳
Se puede observar el funcionamiento del controlador diseñado en simulink

5. Figura 3.Esquema en Simulink
Figura 4.Señal de salida del sistema y señal del controlador
Conclusiones se puede observar que aumenta el máximo sobre impulso (overshoot), y el
tiempo de establecimiento se mantiene en comparación con los otros métodos de
digitalización antes realizados.