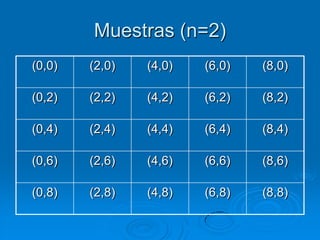
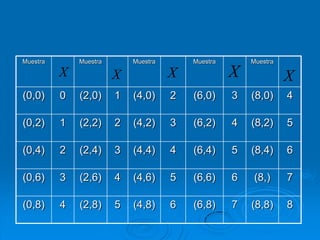
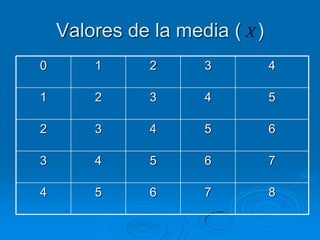
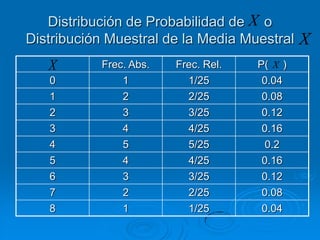
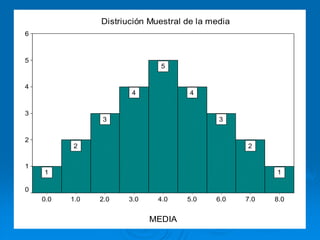
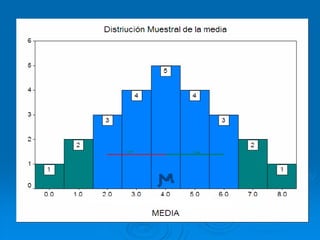
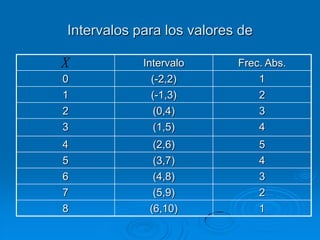
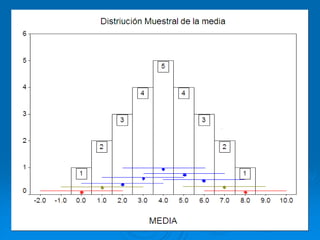
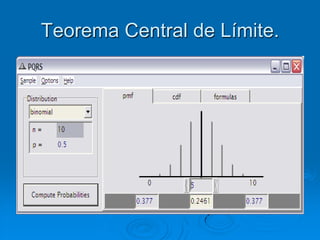
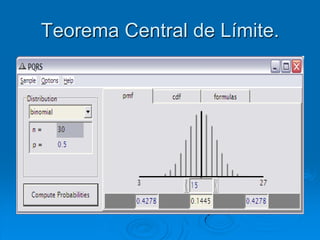
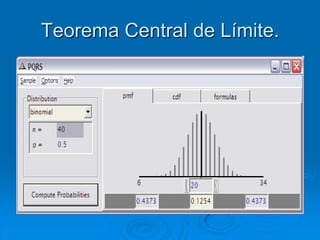
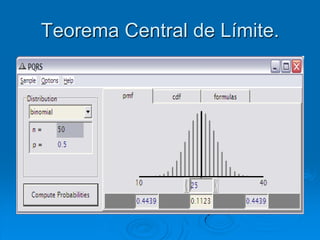
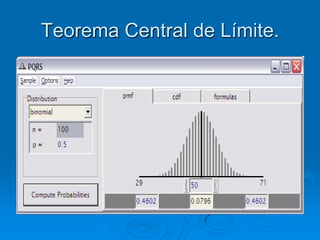
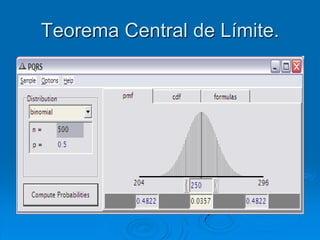
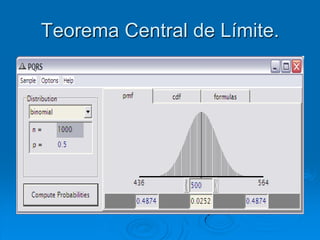
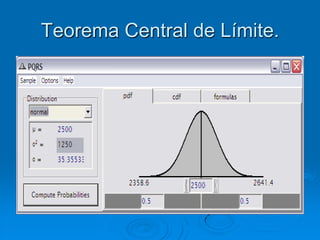
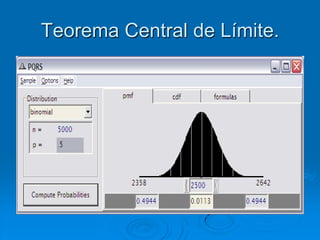
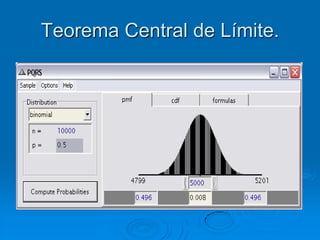
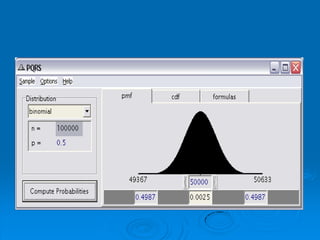
El documento describe la distribución de probabilidad de la media muestral para una población con valores de {0,2,4,6,8}. Se muestran las 25 muestras posibles de tamaño 2 tomadas con reemplazo y sus respectivas medias muestrales. Luego, se presenta la distribución de probabilidad de la media muestral, que indica la probabilidad de que la media tome cada valor posible. Finalmente, se discute cómo el teorema central del límite establece que la distribución muestral de la media converge a una distribución normal

1. DITRIBUCIÓN DE
PROBABILIDAD DE LA
MEDIA.
MC Ma. Guadalupe Sánchez González

2. 2
 Población: {0,2,4,6,8} 4 8
X X
5 5
2
Xi (Xi )
2
X
1
4 X
1
8
N N
 Supóngase que se toman muestras de tamaño
dos n=2, al azar con reemplazo.

3. Muestras (n=2)
(0,0) (2,0) (4,0) (6,0) (8,0)
(0,2) (2,2) (4,2) (6,2) (8,2)
(0,4) (2,4) (4,4) (6,4) (8,4)
(0,6) (2,6) (4,6) (6,6) (8,6)
(0,8) (2,8) (4,8) (6,8) (8,8)

4.  Se pueden obtener 25 muestras posibles.
 Al se tomadas aleatoriamente y por lo
tanto cualquiera de ellas tiene igual
probabilidad de ser seleccionada.
 En este caso en particular:
 1/25=0.04

5. Muestra Muestra Muestra Muestra Muestra
X X X X X
(0,0) 0 (2,0) 1 (4,0) 2 (6,0) 3 (8,0) 4
(0,2) 1 (2,2) 2 (4,2) 3 (6,2) 4 (8,2) 5
(0,4) 2 (2,4) 3 (4,4) 4 (6,4) 5 (8,4) 6
(0,6) 3 (2,6) 4 (4,6) 5 (6,6) 6 (8,) 7
(0,8) 4 (2,8) 5 (4,8) 6 (6,8) 7 (8,8) 8

6. Valores de la media ( X )
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8

7. Distribución de Probabilidad de X o
Distribución Muestral de la Media Muestral X
X Frec. Abs. Frec. Rel. P( X )
0 1 1/25 0.04
1 2 2/25 0.08
2 3 3/25 0.12
3 4 4/25 0.16
4 5 5/25 0.2
5 4 4/25 0.16
6 3 3/25 0.12
7 2 2/25 0.08
8 1 1/25 0.04

8. Distriución Muestral de la media
6
5
5
4
4 4
3
3 3
2
2 2
1
1 1
0
0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
MEDIA

9. Distribución de Probabilidad de X o
Distribución Muestral de la Media X
 Es un cuadro, gráfica o una ecuación que
muestra los valores que toma la media muestral
( X ) y con que probabilidad toma ese valor.

10. 25
 Media de la Xi
1
distribución muestral. X
25 25
Xi
X
1
4
25
25
 Varianza de la (Xi X
)2
2 1
distribución muestral. X
25
25
2
(Xi X
) 2
8
2
X
1 X
4
25 n 2

11. Error Estándar
 El error estándar, es la desviación estándar de la
distribución muestral de la media.
25
2
(Xi X
) 2
8
2
X
1 X
4 2
25 n 2

12.  ¿Qué pasa si se
construye un intervalo X
1 X
a un error estándar 1 y 1
X X X X
de la media
poblacional?
4 2 y 4 2
2 y 6
2 6

13.  ¿Cuántos valores que toma X , caen dentro de
este intervalo?
X
1 X
X
1 X
y X
1 X

15.  Se encuentran 19 de los 25 valores que toma
…X
X
 Es decir el 76% de los valores de …, se
encuentran a una desviación estándar de la
media.

16.  ¿De que sirve saber que el 76% de los valores
de la media ( X ) se encuentran alrededor de
(a una desviación estándar) si en la realidad no
conozco a , sino sólo un valor de X ?

17.  Supóngase que ahora se construirán intervalos
alrededor de todos los posibles valores de X .
X 1 X
X 1 X
y X 1 X

18. Intervalos para los valores de
X Intervalo Frec. Abs.
0 (-2,2) 1
1 (-1,3) 2
2 (0,4) 3
3 (1,5) 4
4 (2,6) 5
5 (3,7) 4
6 (4,8) 3
7 (5,9) 2
8 (6,10) 1

20.  ¿Cuántos intervalos construidos alrededor de la
media muestral ( X ) contienen al parámetro ( )
?
 19 de los 25 intervalos construidos alrededor de
la media muestral contienen al parámetro, esto
es, el 76% de los intervalos calculados alrededor
de X contienen a

21.  Es decir, de cada 100 muestras que se tomen
de dicha población, o sea de cada 100
intervalos que se formen alrededor de la media
muestral X , el 76% contendrá a la media
poblacional .
P( X 1 X
X 1 X
) 0.76

22. Intervalo de Confianza
P( X 1 X
X 1 X
) 0.76
 Intervalo de confianza
X 1 X para
0.76  Confianza
1 X  Cota del error
estimación o precisión
de

23. INTERVALOS DE CONFIANZA
1 1
2 s2 X Y t n1/ 2n2 2 s2
p 1
X Z 1 n1 n2
n
2 s2 /2 s12 2
s2
X tn 1 1 X Y Z 1
n n1 n2
ˆˆ
pq 2 ˆ ˆ
p1q1 ˆ ˆ
p2 q2
ˆ
p Z 2
1 ˆ
p1 ˆ
p2 Z 1
n n1 n2
2
sd /2 sd2
Xd t n/ 21 1 Xd Z 1
n n
23

24. Teorema Central de Límite.
 Independiente de cual sea la distribución de
probabilidad de la característica de interés en
2
una población determinada ( , ) , si se toman
X
muestras grandes, la distribución muestral de la
media es una distribución normal, con media (
2
la de la población original) y varianzaX
.
n

25. Teorema Central de Límite.

26. Teorema Central de Límite.

27. Teorema Central de Límite.

28. Teorema Central de Límite.

29. Teorema Central de Límite.

30. Teorema Central de Límite.

31. Teorema Central de Límite.

32. Teorema Central de Límite.

33. Teorema Central de Límite.

34. Teorema Central de Límite.

35. Teorema Central de Límite.

36. Teorema Central de Límite.

37. Teorema Central de Límite.

38. Teorema Central de Límite.

39. Teorema Central de Límite.

41. ESTIMACIÓN
 Es el procedimiento mediante el cual se
obtiene un valor que es muy parecido al
parámetro, o un rango de valores entre los
cuales se encuentra el parámetro.
• Estimación Puntual
• Estimación por intervalo (Intervalos de
Confianza).