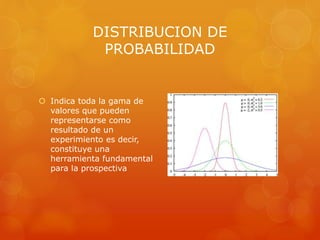
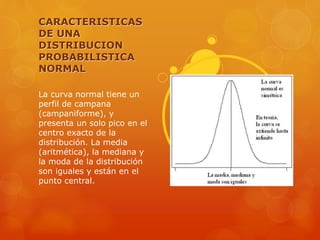
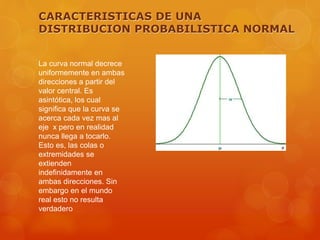
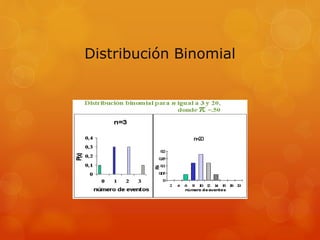
Este documento trata sobre diferentes distribuciones de probabilidad como la normal, binomial, Bernoulli y gamma. Explica que la distribución normal es muy importante debido a que muchas variables siguen este patrón y permite modelar fenómenos naturales. También define las características de una distribución probabilística normal y provee ejemplos de cómo aplicar las distribuciones binomial y Bernoulli.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACION
SUPERIOR
BARQUISIMETO EDO. LARA
INSTITUTO UNIVERSITARIO TECNOLOGICO ANTONIO
JOSE DE SUCRE- EXTENSION BARQUISIMETO
DISTRIBUCION DE
PROBABILIDAD
LUISA R. TERAN C.
C.I : 22.186.522

2. DISTRIBUCION DE
PROBABILIDAD
 Indica toda la gama de
valores que pueden
representarse como
resultado de un
experimiento es decir,
constituye una
herramienta fundamental
para la prospectiva

3. FUNCION DE DISTRIBUCION
 En estadística y probabilidad se llama distribución normal,
distribución de Gauss o distribución gaussiana, a una de las
distribuciones de probabilidad de variable continua que con más
frecuencia aparece aproximada en fenómenos reales.
 La gráfica de su función de densidad tiene una forma acampanada y
es simétrica respecto de un determinado parámetro estadístico.
Esta curva se conoce como campana de Gauss y es el gráfico de
una función gaussiana.
 La importancia de esta distribución radica en que permite modelar
numerosos fenómenos naturales, sociales y psicológicos. Mientras
que los mecanismos que subyacen a gran parte de este tipo de
fenómenos son desconocidos, por la enorme cantidad de variables
incontrolables que en ellos intervienen, el uso del modelo normal
puede justificarse asumiendo que cada observación se obtiene como
la suma de unas pocas causas independientes.
 De hecho, la estadística descriptiva sólo permite describir un
fenómeno, sin explicación alguna. Para la explicación causal es
preciso el diseño experimental, de ahí que al uso de la estadística
en psicología y sociología sea conocido como método correlacional

4. FUNCION DE DISTRIBUCION
 A medida que aumentamos
la cantidad de
observaciones que tomamos
de la población, podemos
construir nuestro gráfico con
un número mayor de
intervalos, aunque de menor
amplitud (El rango total
cubierto por la población es
el mismo

5. FUNCIÓN DE PROBABILIDAD
(V. DISCRETAS)
Asigna a cada posible valor de una
variable discreta su probabilidad.
Recuerda los conceptos de frecuencia
relativa y diagrama de barras.
Ejemplo
Número de caras al lanzar 3 monedas.

6. Ejemplo Distribución
 En una cuidad se estima que la temperatura maxima en
el mes de de Octubre si una distribución normal, con
media 23° y desviación Típica 5°.
 Podemos tomar como ejemplo para la temperatura o
humedad que se presente en los meses mas lluvioso del
año.

7. DISTRIBUCION NORMAL
.

8. DISTRIBUCION NORMAL
 Sin duda la distribución
continua de probabilidad más
importante, por la frecuencia
con que se encuentra y por sus
aplicaciones teóricas, es la
distribución normal,
gaussiana o de Laplace-
Gauss. Fue descubierta y
publicada por primera vez en
1733 por De Moivre. A la misma
llegaron, de forma
independiente, Laplace (1812) y
Gauss (1809), en relación con
la teoría de los errores de
observación astronómica y física
Karl F. Gauss
(1777-1855)

9. DISTRIBUCION NORMAL
• Muchas variables aleatorias continuas presentan una función de
densidad cuya gráfica tiene forma de campana.
• En otras ocasiones, al considerar distribuciones binomiales, tipo
B(n,p), para un mismo valor de p y valores de n cada vez
mayores, se ve que sus polígonos de frecuencias se aproximan
a una curva en "forma de campana".
• En resumen, la importancia de la distribución normal se debe a
que hay muchas variables asociadas a fenómenos naturales
que siguen el modelo de la normal

10. CARACTERISTICAS
DE UNA
DISTRIBUCION
PROBABILISTICA
NORMAL
La curva normal tiene un
perfil de campana
(campaniforme), y
presenta un solo pico en el
centro exacto de la
distribución. La media
(aritmética), la mediana y
la moda de la distribución
son iguales y están en el
punto central.

11. CARACTERISTICAS DE UNA
DISTRIBUCION PROBABILISTICA NORMAL
La curva normal decrece
uniformemente en ambas
direcciones a partir del
valor central. Es
asintótica, los cual
significa que la curva se
acerca cada vez mas al
eje x pero en realidad
nunca llega a tocarlo.
Esto es, las colas o
extremidades se
extienden
indefinidamente en
ambas direcciones. Sin
embargo en el mundo
real esto no resulta
verdadero

12. DISTRIBUCION DE
BERNOULLI

13. DISTRIBUCION DE
BERNOULLI
Consiste en realizar un experimento
aleatorio una sola vez y observar si cierto
suceso ocurre o no, siendo p la
probabilidad de que esto sea asi (éxito) y
q=1-p el que no lo sea (fracaso)

14. DISTRIBUCION DE BERNOULLI
 En realidad no se trata mas que una que unicamente
puede tomar dos modalidades, es por ello que el heho
de llamar éxito o fracaso a los posibles resultados de las
pruebas de resultados de las pruebas del resultado.
Podriamos por tanto definir este experimento medianta
una formula

15. Propiedades de un
experimento de Bernoulli
En cada prueba del experimento sólo
hay dos posibles resultados: éxitos o
fracasos.
2 - El resultado obtenido en cada
prueba es independiente de los
resultados obtenidos en pruebas
anteriores.
3 - La probabilidad de un suceso es
constante, la representamos por p, y
no varía de una prueba a otra. La
probabilidad del complemento es 1-
p y la representamos por q .

16. Ejemplo de Distribucion Bernoulli
 Cuando se lanza un dado en un juego de mesa hay una
probabilidad de 1/6 de que salga 6. Sea x=1 si el dado
cae seis y x=0 en cualquier otro caso. ¿’Cual es la
distribucion de X?
 Este ejemplo es muy comun en los juegos de mesas en
la vida cotidiana.

17. Distribución Binomial

18. Distribución binomial
 La distribución de probabilidad binomial es un ejemplo de
distribución de probabilidad discreta.
 Esta formada por una serie de experimentos de Bernoulli. Los
resutados de cada experimento son mutuamente excluyentes.
 Para contruirla necesitamos:
 1 - la cantidad de pruebas n
 2 - la probabilidad de éxitos p
 3 - utilizar la función matemática.

19. La función
 A continuación vemos La función de probabilidad de la distribución
Binomial, también denominada Función de la distribución de
Bernoulli:
 k - es el número de aciertos.
 n - es el número de experimentos.
 p - es la probabilidad de éxito, como por ejemplo, que salga
"cara" al lanzar la moneda.
 1-p - también se le denomina como “q ”

20. Ejemplos Aplicar
 Se lanza al aire una modena diez veces.
 Esta distribución es de gran ayuda para la vida cotidiana,
ya puede aplicar en caso de un técnico superior ; el
porcentaje de personal obrero los cuales están o no
propenso para una enfermedad ergónoma, sea por el
movimiento repetitivo en medio ambiente de trabajo

21. DISTRIBUCION GAMMA
 En estadistica la distribucion gamma es una distribucion
de probabilidad continua con dos parametros k y cuya
funcion de densidad para valores x > es
 Aquí e es el es la funcion gamma. Para valores la que aquella es (k) =
(k-1)! ( el factorial de k – 1). En este caso – por ejemplo para describir
un proceso de Poisson- se llama la distribucion Erlang con un
parametro =1 /