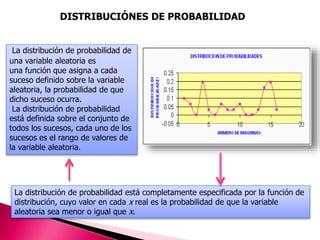
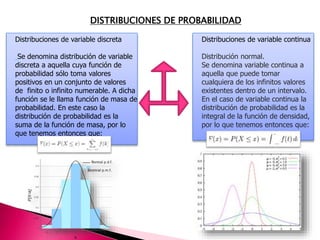
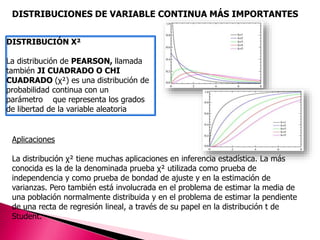
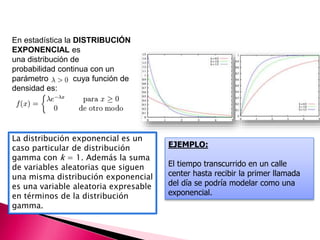
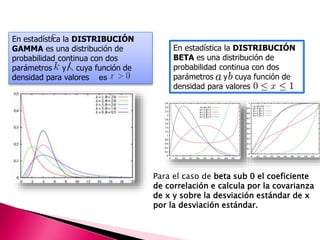
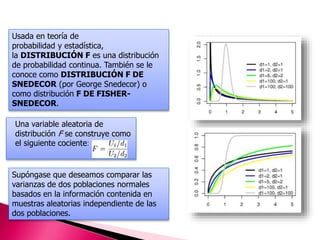
Este documento describe las distribuciones de probabilidad más importantes, tanto para variables discretas como continuas. Explica que una distribución de probabilidad asigna valores de probabilidad a los posibles resultados de una variable aleatoria. Luego define distribuciones como la binomial, Poisson, normal, exponencial y F, y describe sus usos en estadística e inferencia.

1. República bolivariana de Venezuela
Ministerio del poder popular para la educación
I.U.T Antonio José de sucre
Barquisimeto- edo. Lara
DISTRIBUCIÓN DE PROBABILIDAD
Integrante:
WILCARIS QUIROZ C.I: 22.270.440
ESTADISTICA APLICADA

2. DISTRIBUCIÓNES DE PROBABILIDAD
La distribución de probabilidad de
una variable aleatoria es
una función que asigna a cada
suceso definido sobre la variable
aleatoria, la probabilidad de que
dicho suceso ocurra.
La distribución de probabilidad
está definida sobre el conjunto de
todos los sucesos, cada uno de los
sucesos es el rango de valores de
la variable aleatoria.
La distribución de probabilidad está completamente especificada por la función de
distribución, cuyo valor en cada x real es la probabilidad de que la variable
aleatoria sea menor o igual que x.

3. DISTRIBUCIONES DE PROBABILIDAD
Distribuciones de variable discreta
Se denomina distribución de variable
discreta a aquella cuya función de
probabilidad sólo toma valores
positivos en un conjunto de valores
de finito o infinito numerable. A dicha
función se le llama función de masa de
probabilidad. En este caso la
distribución de probabilidad es la
suma de la función de masa, por lo
que tenemos entonces que:
Distribuciones de variable continua
Distribución normal.
Se denomina variable continua a
aquella que puede tomar
cualquiera de los infinitos valores
existentes dentro de un intervalo.
En el caso de variable continua la
distribución de probabilidad es la
integral de la función de densidad,
por lo que tenemos entonces que:

4. DISTRIBUCIONES DE VARIABLE DISCRETA MÁS IMPORTANTES:
LA DISTRIBUCIÓN BINOMIAL es
una distribución de
probabilidad discreta que cuenta el
número de éxitos en una secuencia
de n ensayos
de Bernoulli independientes entre sí,
con una probabilidad fija p de
ocurrencia del éxito entre los
ensayos.
La siguiente situación es un ejemplo
de experimentos que pueden
modelizarse por esta distribución:
Se lanza un dado diez veces y se
cuenta el número X de tres
obtenidos: entonces X ~ B (10,
1/6).
LA DISTRIBUCIÓN BINOMIAL
NEGATIVA es una distribución de
probabilidad discreta que incluye a
la distribución de Pascal.
El número de experimentos de Bernoulli de
parámetro independientes realizados hasta
la consecución del k-ésimo éxito es una
variable aleatoria que tiene una distribución
binomial negativa con parámetros k y
Ejemplo:
En un proceso de manufactura se sabe
que un promedio de 1 en cada 10
productos es defectuoso, ¿cual es la
probabilidad que el quinto (5) artículo
examinado sea el primero (1) en estar
defectuoso?. La solución es: X= artículos
defectuosos P= 1/10 = 0,1 q= 1- 0,1 =
0,9 x= 5 ensayos K= 1 b*(5;1,0.1)=(5-
11-1)(0.1)^1*(0.9)^5-1= b*(5;1,0.1)=
6.6% de probabilidad que el quinto
elemento extraído sea el primero en estar

5. la distribución de Poisson es una distribución
de probabilidad discreta que expresa, a partir de
una frecuencia de ocurrencia media, la
probabilidad de que ocurra un determinado
número de eventos durante cierto período de
tiempo. Concretamente, se especializa en la
probabilidad de ocurrencia de sucesos con
probabilidades muy pequeñas, o sucesos "raros".
Ejemplo
Si el 2% de los libros encuadernados en cierto taller tiene
encuadernación defectuosa, para obtener la probabilidad de que 5 de
400 libros encuadernados en este taller tengan encuadernaciones
defectuosas usamos la distribución de Poisson. En este caso
concreto, k es 5 y, λ, el valor esperado de libros defectuosos es el 2% de
400, es decir, 8. Por lo tanto, la probabilidad buscada es

6. DISTRIBUCIÓN GEOMÉTRICA
En teoría de
probabilidad y estadística,
la distribución geométrica es
cualquiera de las dos distribuciones
de probabilidad discretas siguientes:
la distribución de probabilidad del
número X del ensayo de
Bernoulli necesaria para obtener un
éxito, contenido en el conjunto { 1,
2, 3,...} o
la distribución de probabilidad del
número Y = X − 1 de fallos antes del
primer éxito, contenido en el
conjunto { 0, 1, 2, 3,... }.
Cual de éstas es la que uno llama
"la" distribución geométrica, es una
cuestión de convención y
conveniencia.
DISTRIBUCIÓN
HIPERGEOMÉTRICA
es una distribución discreta
relacionada con muestreos
aleatorios y sin reemplazo.
Supóngase que se tiene una
población de N elementos de los
cuales, d pertenecen a la
categoría A y N-d a la B. La
distribución hipergeométrica
mide la probabilidad de
obtener x ( ) elementos de la
categoría A en una muestra sin
reemplazo den elementos de la
población original.

7. DISTRIBUCIONES DE VARIABLE CONTINUA MÁS IMPORTANTES
DISTRIBUCIÓN Χ²
La distribución de PEARSON, llamada
también JI CUADRADO O CHI
CUADRADO (χ²) es una distribución de
probabilidad continua con un
parámetro que representa los grados
de libertad de la variable aleatoria
Aplicaciones
La distribución χ² tiene muchas aplicaciones en inferencia estadística. La más
conocida es la de la denominada prueba χ² utilizada como prueba de
independencia y como prueba de bondad de ajuste y en la estimación de
varianzas. Pero también está involucrada en el problema de estimar la media de
una población normalmente distribuida y en el problema de estimar la pendiente
de una recta de regresión lineal, a través de su papel en la distribución t de
Student.

8. En estadística la DISTRIBUCIÓN
EXPONENCIAL es
una distribución de
probabilidad continua con un
parámetro cuya función de
densidad es:
La distribución exponencial es un
caso particular de distribución
gamma con k = 1. Además la suma
de variables aleatorias que siguen
una misma distribución exponencial
es una variable aleatoria expresable
en términos de la distribución
gamma.
EJEMPLO:
El tiempo transcurrido en un calle
center hasta recibir la primer llamada
del día se podría modelar como una
exponencial.

9. La DISTRIBUCIÓN T (DE
STUDENT) es una distribución
de probabilidad que surge del
problema de estimar
la media de
una población normalmente
distribuida cuando el tamaño de
la muestra es pequeño.
Aparece de manera natural al
realizar la prueba t de Student para
la determinación de las diferencias
entre dos medias muestrales y para
la construcción del intervalo de
confianza para la diferencia entre
las medias de dos poblaciones
cuando se desconoce la desviación
típica de una población y ésta debe
ser estimada a partir de los datos
de una muestra.
DISTRIBUCIÓN
NORMAL, DISTRIBUCIÓN DE
GAUSS O DISTRIBUCIÓN
GAUSSIANA,
a una de las distribuciones de
probabilidad de variable
continua que con más frecuencia
aparece aproximada en
fenómenos reales.
La gráfica de su función de
densidad tiene una forma
acampanada y es simétrica
respecto de un
determinado parámetro
estadístico. Esta curva se conoce
como campana de Gauss y es el
gráfico de una función
gaussiana.

10. En estadística la DISTRIBUCIÓN
GAMMA es una distribución de
probabilidad continua con dos
parámetros y cuya función de
densidad para valores es
En estadística la DISTRIBUCIÓN
BETA es una distribución de
probabilidad continua con dos
parámetros y cuya función de
densidad para valores
Para el caso de beta sub 0 el coeficiente
de correlación e calcula por la covarianza
de x y sobre la desviación estándar de x
por la desviación estándar.

11. Usada en teoría de
probabilidad y estadística,
la DISTRIBUCIÓN F es una distribución
de probabilidad continua. También se le
conoce como DISTRIBUCIÓN F DE
SNEDECOR (por George Snedecor) o
como distribución F DE FISHER-SNEDECOR.
Una variable aleatoria de
distribución F se construye como
el siguiente cociente:
Supóngase que deseamos comparar las
varianzas de dos poblaciones normales
basados en la información contenida en
muestras aleatorias independiente de las
dos poblaciones.