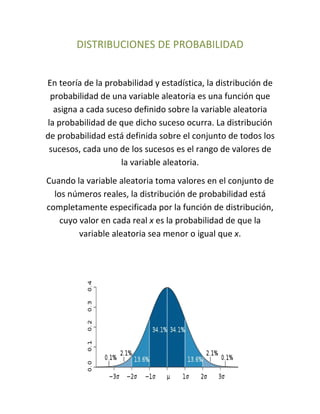
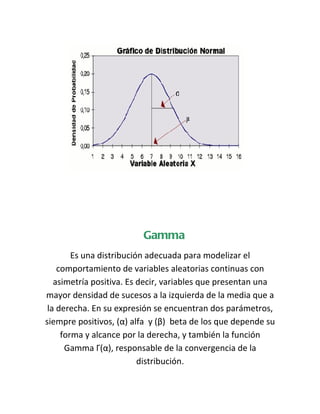
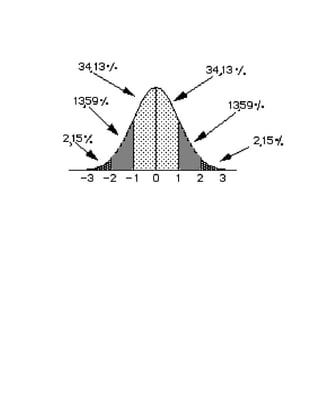
Este documento presenta varias distribuciones de probabilidad importantes como la binomial, Poisson, normal, t student y gamma. Explica que la distribución de probabilidad de una variable aleatoria asigna probabilidades a los posibles resultados y está definida por la función de distribución. También provee ejemplos para ilustrar cómo se aplican estas distribuciones en diferentes contextos estadísticos y de toma de decisiones.

2. DISTRIBUCIONES DE PROBABILIDAD
En teoría de la probabilidad y estadística, la distribución de
probabilidad de una variable aleatoria es una función que
asigna a cada suceso definido sobre la variable aleatoria
la probabilidad de que dicho suceso ocurra. La distribución
de probabilidad está definida sobre el conjunto de todos los
sucesos, cada uno de los sucesos es el rango de valores de
la variable aleatoria.
Cuando la variable aleatoria toma valores en el conjunto de
los números reales, la distribución de probabilidad está
completamente especificada por la función de distribución,
cuyo valor en cada real x es la probabilidad de que la
variable aleatoria sea menor o igual que x.

3. Bernoulli
Un experimento de Bernoulli se caracteriza por ser
dicotómico, esto es, sólo son posibles dos resultados. A
uno de estos se denomina éxito y tiene una probabilidad
de ocurrencia p y al otro, fracaso, con una probabilidad q =
1 - p. En la distribución binomial el anterior experimento se
repite n veces, de forma independiente, y se trata de
calcular la probabilidad de un determinado número de
éxitos. Para n = 1, la binomial se convierte, de hecho, en
una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una
distribución binomial de parámetros n y p, se escribe:
La distribución binomial es la base del test
binomialde significación estadística.

4. Binomial
La distribución binomial esta asociada a experimentos del
siguiente tipo:
Realizamos n veces cierto experimento en el que
consideramos solo la posibilidad de éxito o fracaso.
La obtención de éxito o fracaso en cada ocasión es
independiente de la obtención de éxito o Fracaso en las
demás ocasiones.
La probabilidad de obtener éxito o fracaso siempre es la
misma en cada ocasión.
Veámoslo con un ejemplo
Tiramos un dado 7 veces y contamos el numero de cincos
que obtenemos. ¿Cual es la probabilidad de obtener tres
cincos?.
Este es un típico ejemplo de distribución binomial, pues
estamos repitiendo 7 veces el experimento de lanzar un
dado. ¿Cual es nuestro ´éxito?.
Evidentemente, sacar un 5, que es en lo que nos fijamos.
El fracaso, por tanto, seria no sacar 5, sino sacar cualquier
otro numero.

5. Por tanto, Éxito = E = “sacar un 5” = ´ ⇒p(E) =
1
6
Fracaso = F = “no sacar un 5” =⇒p(F) =
5
6
Para calcular la probabilidad que nos piden, observemos
que nos dicen que sacamos 3 cincos y por lo tanto tenemos
3 ´éxitos y 4 fracasos, ¿de cuantas maneras pueden darse
estas posibilidades?.
Podríamos sacar 3 cincos en las 3 primeras tiradas y luego 4
tiradas sin sacar cinco, es decir: EEEFFFF
Pero también podríamos sacar EFEFFFE, es decir que en
realidad estamos calculando la E es exito y la F es fracaso

6. Poisson
En teoría de probabilidad y estadística, la distribución de
Poisson es una distribución de probabilidad discreta que
expresa, a partir de una frecuencia de ocurrencia media, la
probabilidad que ocurra un determinado número de
eventos durante cierto periodo de tiempo.
La función de masa de la distribución de Poisson es
Para qué sirve conocer que algo es Poisson?

7. Porque si se tiene caracterizado el comportamiento
probabilístico de un fenómeno aleatorio, podemos
contestar preguntas como:
• Qué probabilidad hay de que lleguen más de 15
clientes al banco en un intervalo de 5 minutos de
duración?
• Qué probabilidad hay de que suceda por lo menos una
falla en un tramo de 1km de tubería de gas?
• Qué probabilidad hay de que en un estanque de cultivo
de camarón, haya más de media tonelada?
• Qué probabilidad hay de que en un área de 1km se
encuentren más de 3 brotes de una enfermedad?
Normal
Se le llama distribución normal, distribución de Gauss o
distribución gaussiana, a una de las distribuciones de
probabilidad de variable continua que con más frecuencia
aparece aproximada en fenómenos reales.
La gráfica de su función de densidad tiene una forma
acampanada y es simétrica respecto de un determinado
parámetro. Esta curva se conoce como campana de Gauss y
e es el gráfico de de una función gaussiana.
ejemplo de alguna grafica seria:

8. Gamma
Es una distribución adecuada para modelizar el
comportamiento de variables aleatorias continuas con
asimetría positiva. Es decir, variables que presentan una
mayor densidad de sucesos a la izquierda de la media que a
la derecha. En su expresión se encuentran dos parámetros,
siempre positivos, (α) alfa y (β) beta de los que depende su
forma y alcance por la derecha, y también la función
Gamma Γ(α), responsable de la convergencia de la
distribución.

9. La distribución gamma se puede caracterizar del modo
siguiente: si se está interesado en la ocurrencia de un
evento generado por un proceso de Poisson de media
lambda, la variable que mide el tiempo transcurrido hasta
obtener n ocurrencias del evento sigue una distribución
gamma con parámetros a=n×lambda (escala) y p=n (forma).
Se denota Gamma(a,p).
Por ejemplo, la distribución gamma aparece cuando se
realiza el estudio de la duración de elementos físicos
(tiempo de vida).
Esta distribución presenta como propiedad interesante la
“falta de memoria”. Por esta razón, es muy utilizada en las
teorías de la fiabilidad, mantenimiento y fenómenos de
espera (por ejemplo en una consulta médica “tiempo que
transcurre hasta la llegada del segundo paciente”), la teoría
de la cola, electricidad, procesos industriales.

10. T student
La distribución normal es una distribución de probabilidad.
Lo que significa que podemos decir cuál es la probabilidad

11. de ocurrencia de un evento aleatorio proveniente de una
población normal.
Por ejemplo, mirando el gráfico 1, podemos decir que la
probabilidad de extraer aleatoriamente un caso que se
encuentre entre la media y -1 desviación estandar es de
34,13%. ¿Cierto? Si lo que se sabe es la probabilidad de un
evento, digamos que sabemos que el caso elegido tenía
menos de un 2,15% de probabilidades de ocurrir eso
significa que debe haber obtenido una puntuación Z mayor
a 2 o menor que -2.
Siguiendo esta lógica y usando el Gráfico 1, ¿Cuál sería la
probabilidad de ocurrencia de un caso con una puntuación Z
igual 1,5? ¿Cuál sería el puntaje z de un caso que está
encima del 84.26% del resto de la población? ¿Cuál es la
probabilidad de ocurrencia de dicho caso?
Estas estimaciones pueden hacerse con mucha mayor
precisión si se ocupan las computadoras o las tablas de
probabilidades y puntuaciones Z. Abajo tenemos una de
estas tablas (Tabla 1). Esta tabla permite identificar el
puntaje Z para una probabilidad dada. La probabilidad se
obtiene sumando al valor de la columna izquierda el valor
del encabezado de la columna. Por ejemplo, la probabilidad
del 8% se obtiene al elegir el valor .00 de la columna
izquierda y buscar el valor .08 en el encabezado de la
columna. Se considera este 8% distribuido en los dos
extremos de la desviación, 4% en el extremo inferior y 4%
en el extremo superior.