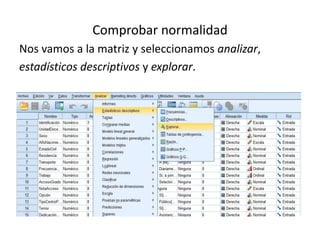
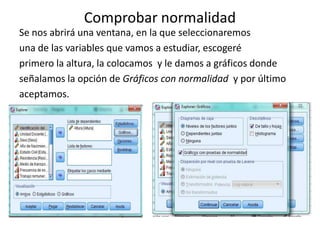
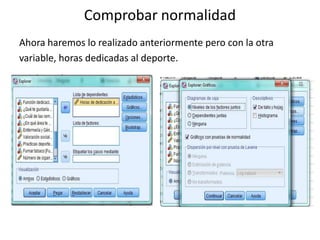
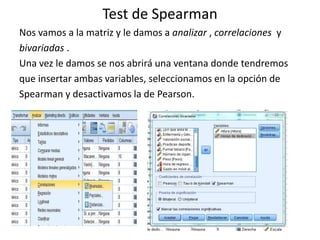
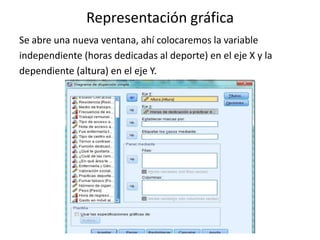
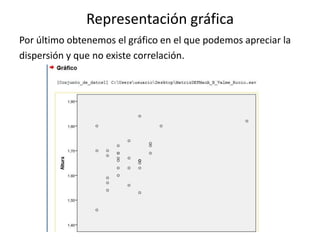
Este documento resume los pasos para analizar la correlación entre dos variables cuantitativas tomadas de un cuestionario: la altura y las horas dedicadas al deporte. Explica cómo comprobar la normalidad de distribución de cada variable usando las pruebas de Kolmogorov-Smirnov o Shapiro-Wilk, y luego aplicar la prueba de correlación de Spearman dado que una variable no sigue una distribución normal. Los resultados de la prueba de Spearman no muestran una relación significativa entre las dos variables.

1. Seminario 10

2. 1. Elige dos variables de la matriz de datos del
cuestionario.
Comenta los resultados y represéntalos gráficamente.
Para ver la correlación las dos variables que vamos a
usar deben ser cuantitativas, yo elegiré la altura y las
horas dedicadas al deporte.
Lo siguiente será ver si cada una de las variables siguen
una distribución normal,lo comprobaremos con
kolmogorov o shapiro, para luego elegir el estadístico
de Person (ambas variables siguen distribución normal)
Spearman ( con que tan solo una no siga la normalidad,
usaremos este estadístico).

3. Comprobar normalidad
Nos vamos a la matriz y seleccionamos analizar,
estadísticos descriptivos y explorar.

4. Comprobar normalidad
Se nos abrirá una ventana, en la que seleccionaremos
una de las variables que vamos a estudiar, escogeré
primero la altura, la colocamos y le damos a gráficos donde
señalamos la opción de Gráficos con normalidad y por último
aceptamos.

5. Comprobar normalidad
Se nos abre la página con todas las tablas. Ahora tendremos que
elegir entre kolmogorov y shapiro. En nuestro caso como el
grado de libertad es 50, escogeremos kolmogorov.
Ahora nos fijaremos en el nivel de significación que es 0,200,
mayor que 0,05, por tanto aceptamos la Hₒ,es decir si sigue una
distribución normal.

6. Comprobar normalidad
Ahora haremos lo realizado anteriormente pero con la otra
variable, horas dedicadas al deporte.

7. Comprobar normalidad
Como antes, nos fijamos en el grado de libertad, esta vez es 31
con lo cual cogemos Shapiro, y miramos su significación que nos
resulta 0,000 que es menor que 0,05 con lo cual rechazamos la
Hₒ , es decir esta variable no sigue una distribución normal.
Como una de las variables no sigue una distribución normal el
test que elegiremos será Spearman.

8. Test de Spearman
Nos vamos a la matriz y le damos a analizar , correlaciones y
bivariadas .
Una vez le damos se nos abrirá una ventana donde tendremos
que insertar ambas variables, seleccionamos en la opción de
Spearman y desactivamos la de Pearson.

9. Test de Spearman
Le damos a aceptar y nos sale la correspondiente tabla.
Hₒ : no influye las horas dedicadas al deporte a la altura.
Nos fijamos en el número señalado, 0,298 es un valor positivo ,
la correlación es positiva moderada ya que se encuentra entre 0
y 0,90.

10. Test de Spearman
Ahora nos fijaremos en el valor de sig, que es 0,103 , es mayor
0,05 , aceptamos la Hₒ, lo que indica que no hay relación entre
las variables.
No hay relación entre la altura y las horas dedicadas al deporte.

11. Representación gráfica
Abrimos la matriz y le damos a gráficos, cuadro de diálogo
antiguo, dispersión/puntos. Se nos abrirá otra ventana donde le
daremos a dispersión simple y por último a definir.

12. Representación gráfica
Se abre una nueva ventana, ahí colocaremos la variable
independiente (horas dedicadas al deporte) en el eje X y la
dependiente (altura) en el eje Y.

13. Representación gráfica
Por último obtenemos el gráfico en el que podemos apreciar la
dispersión y que no existe correlación.