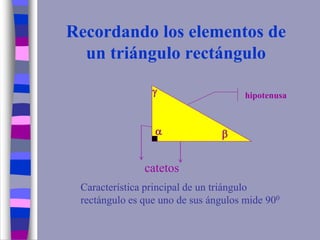
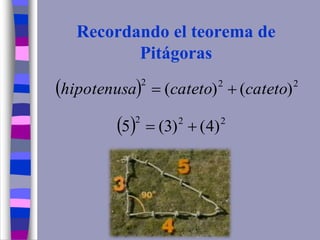
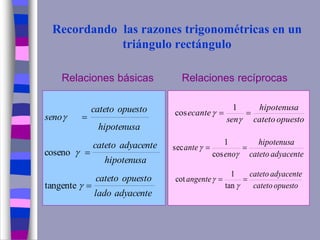
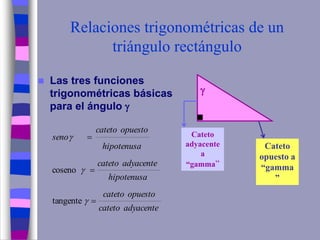
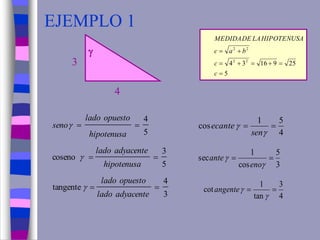
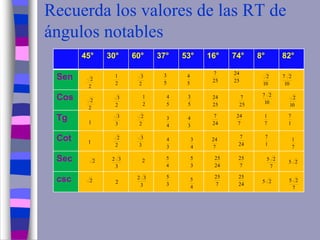
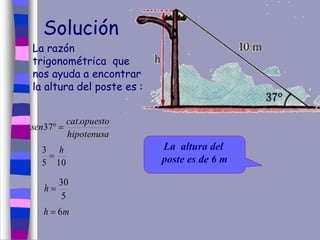
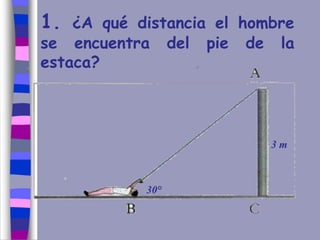
El documento ofrece una explicación sobre la resolución de triángulos rectángulos y el uso del teorema de Pitágoras, así como las funciones trigonométricas básicas. Se incluyen ejemplos prácticos para calcular alturas y distancias en diversas situaciones trigonométricas. Además, se plantea una serie de ejercicios para aplicar los conceptos explicados.

1. RESOLUCIÓN DE
TRIÁNGULOS
RECTÁNGULOS
Preparado por:
Prof. Rosa María Cusi Condori

2. Observa el siguiente video…
Haz clic aquí

3. ¿De qué largo tendrá que ser la
escalera para alcanzar el foco,
colocada a una distancia de
1,80m?

4. RESOLUCIÓN DE
TRIÁNGULOS
RECTÁNGULOS

5. Recordando los elementos de
un triángulo rectángulo

hipotenusa


catetos
Característica principal de un triángulo
rectángulo es que uno de sus ángulos mide 900

6. Recordando el teorema de
Pitágoras
  222
)()( catetocatetohipotenusa 
  222
)4()3(5 

7. Recordando las razones trigonométricas en un
triángulo rectángulo
Relaciones básicas Relaciones recíprocas
adyacentelado
opuestocateto
hipotenusa
adyacentecateto
hipotenusa
opuestocateto
seno






tangente
coseno
opuestocateto
hipotenusa
sen
ecante 


1
cos
adyacentecateto
hipotenusa
eno
ante 


cos
1
sec
opuestocateto
adyacentecateto
angente 


tan
1
cot

8. Relaciones trigonométricas de un
triángulo rectángulo
 Las tres funciones
trigonométricas básicas
para el ángulo 

Cateto
adyacente
a
“gamma”
Cateto
opuesto a
“gamma
”
adyacentecateto
opuestocateto
hipotenusa
adyacentecateto
hipotenusa
opuestocateto
seno






tangente
coseno

9. EJEMPLO 1
3
4
tangente
5
3
coseno
5
4



adyacentelado
opuestolado
hipotenusa
adyacentelado
hipotenusa
opuestolado
seno



5
2591634 22
22



c
c
bac
HIPOTENUSALADEMEDIDA

4
3
4
51
cos 


sen
ecante
3
5
cos
1
sec 


eno
ante
4
3
tan
1
cot 

angente

10. Recuerda los valores de las RT de
ángulos notables
45° 30° 60° 37° 53° 16° 74° 8° 82°
Sen
Cos
Tg
Cot
Sec
csc
2
2
1
2
2
2
1
5
4
25
7
25
24
10
2
10
27
2
3
25
24
25
7
3
3
2
2
24
7
7
24
7
1
1
7
2
2
1
2
2
2
1
2
3
3
3
2
2
3
32
3
32
5
4
5
3
5
3
4
3
3
4
4
3
3
4
3
5
3
5
4
5
4
5
24
7
7
24
24
25
24
25
7
25
7
25
10
2
10
27
7
1
1
7
7
25
7
2525
25

11. A resolver
los problemas con
triángulos rectángulos

12. Calcula la altura h del poste
teniendo en cuenta los datos de la
figura.

13. Solución
La razón
trigonométrica que
nos ayuda a encontrar
la altura del poste es :
hipotenusa
opuestocat
sen
.
37 
105
3 h

5
30
h
mh 6
La altura del
poste es de 6 m

14. Ahora te toca a tí

15. ¿A qué distancia el
hombre se encuentra del
pie de la estaca?
1. ¿A qué distancia el hombre
se encuentra del pie de la
estaca?
30°
3 m

16. 2.Calcula la altura del tobogán que
tiene 5 m de longitud y 53º de
inclinación con el piso.

17. 3. Para llegar de un hotel a la cima de una
montaña, fueron necesarios 120 m de cabo
teleférico. El ángulo de inclinación del cabo
es de 37º. ¿Cuál es la altura de la montaña?
37°

18. 4.Determina la altura h de la
imagen
40 m
=37°

19. 5.¿Cuál es
la altura
del suelo al
aro?
1,70m
2,5√2m
45° 45°

20. 6.Una escalera de un camión de bomberos se
puede extender hasta un máximo de 30 m cuando
es levantada a un ángulo máximo de 60º. Se sabe
que la base de la escalera está colocada a 2
metros del piso. ¿Qué altura en relación al piso
puede alcanzar esa escalera?
60°

21. 7. Desde lo alto de una torre de 60 m de altura,
localizada en una isla, se avista una playa bajo un
ángulo de 30º en relación con la horizontal. Para
transportar material de la playa hasta la torre, un
barquero cobra S/. 5,00 por metro recorrido. En
esas condiciones, ¿Cuánto recibe en cada
transporte que hace?

22. 8.Observa la figura y determina
la altura de la Torre Eiffel.
367,2 m
30º 60º

23. 9. Un navío ve un peñasco con un
ángulo de 30º. Avanzando 450 m en
dirección al peñasco, ese ángulo pasa
a ser de 60º. Calcula la altura del
peñasco

24. Gracias.