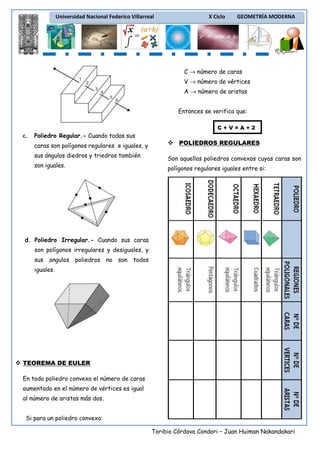
Este documento presenta información sobre diversos temas de geometría moderna como ángulos diedros, poliedros, poliedros regulares y teoremas relacionados. Incluye definiciones, ejemplos y ejercicios resueltos sobre estos temas. El documento fue elaborado por dos estudiantes de la Facultad de Educación de la Universidad Nacional Federico Villarreal para el curso de Geometría Moderna.

1. Universidad Nacional
Federico Villarreal
2013
Facultad de Educación
Matemática - Física
GEOMETRÍA MODERNA
Profesor: Bonilla Salcedo
Tema:
DIEDROS,
TRIEDROS,
POLIEDROS Y
POLIEDROS
REGULARES
INTEGRANTES:
CÓRDOVA CONDORI, TORIBIO
HUIMAN NAKANDAKARI, JUAN
CICLO: X
AÑO: 5TO
AULA: A3-7

2. Universidad Nacional Federico Villarreal
X Ciclo
GEOMETRÍA MODERNA
ÁNGULOS DIEDROS
Q
Es la figura geométrica formada por la unión
de sus semiplanos que tienen una recta en
α
común a la cual se le denomina arista del
θ
α + θ = 180º
ángulo diedro.
P
Arista
A
Notación:
PROYECCIÓN
UN PLANO
Ángulo Diedro AB ó
P
cara
cara
Q
Ángulo Diedro
punto
y
x
B
SOBRE
Por definición la proyección ortogonal de un
P - AB - Q
θ
ORTOGONAL
sobre
un
plano
es
el
pie
de
la
perpendicular trazada de este punto al plano. De
θ: Medida del ángulo
Diedro
esto se concluye que la proyección ortogonal de
cualquier figura geométrica sobre un plano es la
reunión de las proyecciones
ortogonales de todos sus puntos sobre dicho
PLANOS PERPENDICULARES
plano.
Dos planos son perpendiculares, cuando
P
determinan diedros que miden 90º.
L
Q
θ
θ:
θ
P
Medida
del
ángulo diedro.
Si
⇒
Q
m
P’
θ = 90º
P
Q
Sea PP'
Q
⇒
P’ es la proyección del
punto P sobre el plano Q
Observación.- Dos diedros adyacentes son
suplementarios.
Además M es la proyección ortogonal de
L
sobre el plano Q.
Toribio Córdova Condori – Juan Huiman Nakandakari

3. Universidad Nacional Federico Villarreal
X Ciclo
GEOMETRÍA MODERNA
Ángulos Poliedros
POLIEDROS
Poliedro
es
un
sólido
Son los formados en los vértices del
completamente
limitado por polígonos. El mínimo número de
caras que tiene un poliedro es cuatro.
poliedro
Diagonal
Es el segmento que une dos vértices no
situados en la misma cara
CLASIFICACION
1) Por el número de caras:
- Tetraedro: cuando tiene 4 caras
ELEMENTOS DE UN POLIEDRO
- Pentaedro: cuando tiene 5 caras
Los elementos principales de un poliedro son:
- Hexaedro: cuando tiene 6 caras
- Heptaedro: cuando tiene 7 caras
Vértice
- Octaedro: cuando tiene 8 caras
Diagonal
2) Según sus características:
Cara
Arista
a. Poliedro Convexo.-
Cuando cualquiera
de sus secciones planas es un polígono
convexo,
segmento
o
equivalentemente,
que
une
dos
si
el
puntos
cualesquiera del poliedro está totalmente
Caras
contenido en el poliedro.
Son los polígonos que limitan los poliedros.
Aristas
Son las intersecciones de las caras.
Vértice
Son los puntos donde se encuentran las
aristas-
b. Poliedro no convexo.- Cuando alguna de
las secciones planas es un polígono
cóncavo. Al trazar una recta secante
Ángulos Diedros
corta en más de 2 puntos de intersección
Son los formados por dos caras consecutivas.
a su superficie poliédrica.
Toribio Córdova Condori – Juan Huiman Nakandakari

4. Universidad Nacional Federico Villarreal
X Ciclo
GEOMETRÍA MODERNA
C → número de caras
1
V → número de vértices
2
3
A → número de aristas
4
5
6
Entonces se verifica que:
C+V=A+2
c.
Poliedro Regular.- Cuando todas sus
caras son polígonos regulares e iguales, y
sus ángulos diedros y triedros también
son iguales.
POLIEDROS REGULARES
Son aquellos poliedros convexos cuyas caras son
polígonos regulares iguales entre si:
d. Poliedro Irregular.- Cuando sus caras
son polígonos irregulares y desiguales, y
sus
angulos
poliedros no son todos
iguales.
TEOREMA DE EULER
En todo poliedro convexo el número de caras
aumentado en el número de vértices es igual
al número de aristas más dos.
Si para un poliedro convexo:
Toribio Córdova Condori – Juan Huiman Nakandakari

5. Universidad Nacional Federico Villarreal
A) TETRAEDRO: Sus caras son
regiones triangulares equiláteras.
cuatro
X Ciclo
Notación:
GEOMETRÍA MODERNA
Exaedro Regular ABCD – EFGH
Diagonal ( BH ):
l
BH =
O
3
Volumen (V):
v =
l3
Superficie total o Área (A):
C
A = 6l 2
A
G
C) OCTAEDRO: Sus caras son
regiones triangulares equiláteras.
B
ocho
M
Notación: Tetraedro Regular O – ABC
Altura: OG ; siempre cae en el baricentro (G)
OG =
l
6
3
B
Volumen (V):
V =
l3
C
A
2
D
12
Superficie total o Área (A):
A =
l2
3
N
B) HEXAEDRO: Sus caras son seis regiones
cuadradas, también se le denomina cubo.
Notación: Octaedro Regular
M – ABCD – N
Diagonal ( MN ):
MN =
B
l
2
C
Volumen (V):
D
A
V =
F
G
l3
2
3
Superficie total o Área (A):
A = 2l 2 3
E
H
Toribio Córdova Condori – Juan Huiman Nakandakari

6. Universidad Nacional Federico Villarreal
X Ciclo
GEOMETRÍA MODERNA
D) DODECAEDRO: Sus caras son doce
regiones pentagonales iguales.
1. En
un
tetraedro
O-ABC,
OA=BC,
OB=AC y OC=AB, además se cumple
AC>OC>AO. Halla la suma del máximo
y mínimo entero de la cara AOC
Solución
Volumen (V):
V =
5l 3
2
47 + 21 5
10
Superficie total o Área (A):
A = 15l 2
5+2 5
5
E) ICOSAEDRO: Sus caras son veinte
regiones triangulares equiláteras.
a
a>b>c→θ> >
ΔAOC ≈ Δ OAB ≈ Δ CBA (LLL)
→m∠AOC=m∠ OCB= θ
m∠AOC= m∠ACB=
AOC:
Volumen (V):
5a 2
V =
6
7+3 5
2
θ+ + = 180º → + = 180º θ ……. (1)
Por teorema:
Superficie total o Área (A):
<θ<
……. (2)
A = 5a 2 3
De (1) y (2): θ < 180º θ
Toribio Córdova Condori – Juan Huiman Nakandakari

7. Universidad Nacional Federico Villarreal
X Ciclo
θ < 90º
APB:
Por condición:
HAD:
< θ;
<θ
AH=
=
GHD:
Sumando:
< 2θ
GEOMETRÍA MODERNA
=
+
+
…. (1)
…. (2)
en (2):
180º θ < 2θ y 60º < θ
60º < θ < 90º
Simplificando:
luego:
θmin= 61º
θmáx.= 89º
θmin + θmáx = 150º
3. En un poliedro convexo, el numero de
2. Un cuadrado ABCD y un triangulo
caras, mas el numero de vértices, y
rectángulo APB están contenidos en
más el numero de aristas, es 28. Si las
dos planos perpendiculares. Halle la
medidas de los ángulos en todas las
distancia entre el vértice D y el
caras suman 1800º. Hallar el número de
baricentro APB; si se sabe que AP=3,
caras.
PB=4.
Solución
Solución
Dato:
S = 1800º. Pero sabemos que
S = 360º(V-2)
Entonces: 360º(V – 2) = 1800º
V–2=5
V=7
Por el Teorema de Euler:
C+V=A+2
A = C + 5......(1)
Toribio Córdova Condori – Juan Huiman Nakandakari

8. Universidad Nacional Federico Villarreal
Pero por dato también:
X Ciclo
GEOMETRÍA MODERNA
NOC; se cumple que:
En el
C + V + A = 28
C + 7 + A = 28
C + A = 21......(2)
Reemplazando (1) en (2):
C + C + 5 =21
∴
NC=3a
x = 90º
∴
2C = 16
C = 8
5. Se tiene un cuadrado ABCD y un
triangulo
equilátero
pertenecientes
4. Se tiene un exaedro regular ABCD –
a
AMB
dos
planos
perpendiculares. Calcular la medida del
EFGH, donde “O” es centro de la cara
ángulo
ABFE y “M” punto medio de EH.
segmento que une los puntos medios de
Calcular la medida del ángulo COM.
MB y AD.
Solución
Solución
• Los
determinado
segmentos
por
EF
BC
y
y
BC
el
son
alabeados.
En el grafico, observamos que:
• El
ángulo
formado
por
dichos
segmentos es AFE
NC = 3a 2
• En la figura el ΔAEM ≈ ΔEAF
Toribio Córdova Condori – Juan Huiman Nakandakari

9. Universidad Nacional Federico Villarreal
X Ciclo
GEOMETRÍA MODERNA
7. Se tiene un triangulo isósceles AOB,
tal que AO=OB= 6 , se levanta OM
x = 60º
∴
perpendicular al plano determinado por
el triangulo. Calcular la longitud de OM,
si el diedro formado por los planos
6. Por el vértice “B” de un triangulo ABC
recto
en
“B”,
se
levanta
BD
perpendicular al plano determinado por
determinados por los triángulos AMB y
AOB mide 60º.
Solución
el triangulo. Calcular la medida del
ángulo diedro que forman los planos
determinados por los triángulos ADC y
ABC.
Si AB=8, BC=8 3 /3 y BD=3
Solución
Por dato: AO= 6 , OB=ON= 3
Em Δ MON es notable, ya que la
m∠MNO=60º
En consecuencia: x= 3 . 3
∴
x = 3
• Por dato; AB=8, BC=8 3 /3,
entonces por propiedad en el Δ ABC:
8. La suma de las medidas de las cars de
un poliedro convexo es 3600º. Si el
número de aristas excede en 2 al doble
del número de cars. Hallar el número
→ BH=4
• En el Δ DBH: tgx= 3/4
∴
x = 37º
de caras.
Solución
Sabemos que: S=360º(V-2)
Pero: S=3600º
Toribio Córdova Condori – Juan Huiman Nakandakari

10. Universidad Nacional Federico Villarreal
X Ciclo
GEOMETRÍA MODERNA
Entonces: 3600º=360º(V-2)
→ A = 160
→ V-2=10
Reemplazando en (1):
→ V=12
96 + V = 160 + 2
Por dato también: A=2C+2 …(1)
Por el Teorema de Euler:
∴
V = 66
C + V = A + 2…(2)
Reemplazando (1) en (2):
C + V = 2C + 2 + 2
→ C + 12 = 2C + 4
10. Se tiene un tetraedro S-BCD, siendo
los puntos M y N los baricentros de las
caras, además el punto G es el punto de
intersección de los segmentos BM y
SN. Si: SN=12m. Hallar SG.
→
C = 8
Solución
9. Hallar el número de vértices del
poliedro convexo que está limitado por
32 cuadriláteros y 64 triángulos.
Solución
Por el Teorema de Euler:
C + V = A + 2……(1)
Donde:
En la figura sombreada:
C → Nº de caras
Por el Teorema de Menelao:
V → Nº de vértices
m. x . 2n = 2m . GN . 3n
A → Nº de aristas
x = 3(SN – x)
En el problema:
4x = 3(12)
C = 32 + 64
→ C = 96
∴
x = 9m
Además sabemos que:
Toribio Córdova Condori – Juan Huiman Nakandakari

11. Universidad Nacional Federico Villarreal
11. En
la
figura
birrectángulo
BP=PC=2
P-ABC
donde
es
un
triedro
BPC=120°,
y AP= 2. Hallar el área del
triángulo ABC.
A)
D)
si
X Ciclo
12. En
un
GEOMETRÍA MODERNA
triedro
AOB=BOC= 60°
isósceles
O-ABC,
y el diedro OB mide
90°. calcule la medida de la cara AOC.
A) arc cos (
B)
E)
C)
B) arc cos (
C) arc cos (
D)
arc cos (
E) arc cos (
Solución
Solución
=
+
Por ley de cosenos:
Por prop. del triángulo de 120° :
BP= PC=2
→ BC = 6
=
+
2( 2a)
(2a) cos x
p=
8 cos x = 2
S=
S=
S=
x = arc cos (
13. Los catetos de un triángulo rectángulo
miden 30 cm y 40 cm, se hace girar el
triángulo alrededor de su hipotenusa
Toribio Córdova Condori – Juan Huiman Nakandakari

12. Universidad Nacional Federico Villarreal
hasta
formar
un
diedro
de
60°.
X Ciclo
GEOMETRÍA MODERNA
Solución
Calcular la longitud del segmento que
une los centros de gravedad de las
bases del diedro.
Solución
Por teorema:
70° + 90° + VC
→ VC
70° + 90° + VC
rectángulo BAC
20°
180° → VC
VC
30 (40) = 50 AH; AH =
es equilátero
=
15. En un triedro SABC, el diedro SA es
recto y las caras ASB y ASC son
ángulos de 45°, se pide calcular las
M
caras BSC.
//
Lema de Thales
=
→
(
=8
= 8 m.
14. Dos caras de un triedro miden 115° y
125°.
Determinar entre que valores
Solución
Se traza un plano ABC ⊥ SA
∠BAC = 90° m∠diedro SA
Hacemos SA = a
ΔSAB:
SB =
=a
= SC
puede variar la tercera cara.
Toribio Córdova Condori – Juan Huiman Nakandakari

13. Universidad Nacional Federico Villarreal
(∇rect.SAB = ∇rest.SAC )
X Ciclo
GEOMETRÍA MODERNA
BC =
Como SB = BC = a
ΔMOF.
Δrect. AOB:
Δ BAC:
Observando
OF =
=a
=
, el ∇ BSC es
equilátero, entonces
Δ rect.MOF: MF=
como cateto OF =
∠BSC = 60°
= 2a
de la hipotenusa MF,
∠MFO = 30°
entonces:
α = 90°
30°
α=60°
°
16. Dado un triángulo rectángulo AOB,
recto en O, cuyos catetos OA= OB =
2a, se levanta en O el plano AOB, una
perpendicular sobre la que se toma
OM= a
y se une luego M con los
puntos A y B. Calcular la medida del
ángulo diedro AB.
Solución
Se traza OF ⊥ AB
MF ⊥ AB ( Teor, 3 ⊥s)
∠MFO es m∠ diedro AB
Toribio Córdova Condori – Juan Huiman Nakandakari

14. Universidad Nacional Federico Villarreal
X Ciclo
GEOMETRÍA MODERNA
PROBLEMAS PROPUESTOS
A) 149º
1. ABC, es un triangulo recto en B. ACD,
es un triangulo equilátero contenido en
un plano perpendicular al plano ABC. Si
B) 169º
B) D) 99º
C) 179º
E) 189º
5. Las regiones rectangulares ABCD y
ABMN, determinan un diedro que mide
AC = 8, Hallar BD.
120º, si 2 BM = AB = 2 BC = 2 a. Halle
la distancia “D” al punto medio de MN.
2. De las siguientes proposiciones indicar
verdadero
(V)
o
falso
(F):
A) a
D)
( ) Todo plano perpendicular a la arista
B)
C) 2a
E)
de un diedro es perpendicular a las
caras
del
diedro.
6.
En un exaedro regular ABCD – EFGH
( ) Si una recta es perpendicular a una
cuya arista mide 4m. ¿Calcular la
de las caras de un diedro y paralela a la
distancia entre AF y BH?.
otra cara entonces la medida del
diedro es 90.
7. En un hexaedro regular ABCD – EFGH, con
centro en E y radio EB se traza un arco de
A) VV
B) FV
D) VF
circunferencia que interseca a HC en “P”.
C) FF
E) VV
¿Calcular el ángulo que forma EP con la
cara EFGH?.
3. Se tiene un diedro MN que mide 60º y
un
punto
F
situado
en
su
plano
bisector, si F dista de la arista que une
los planos M y N en 10 u. Calcular la
distancia de F a las caras del diedro.
A) 3 3
D) 10
4.
B) 4
E) 5 3
C) 5
Calcular el mayor valor entero que
puede tomar una de las caras de un
triedro birrectángulo.
8. En un octaedro regular M-ABCD-N,
cuya arista mide 6m, G es baricentro
de la cara DMC. ¿Calcular AG?
9. Calcular el volumen de un cubo donde el
área y el volumen son numéricamente
iguales.
10. En un octaedro regular, de arista “a”,
hallar la distancia del centro a una
cara.
Toribio Córdova Condori – Juan Huiman Nakandakari