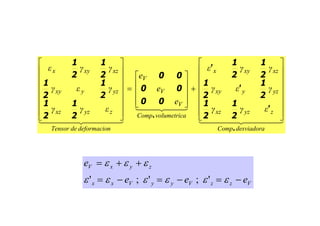
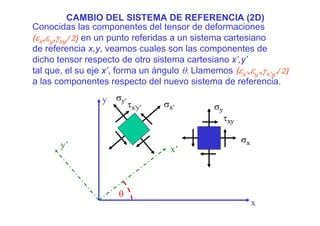
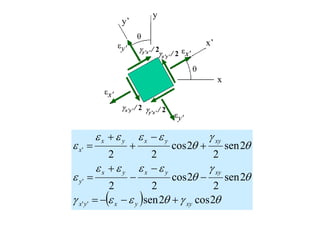
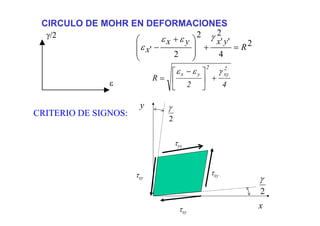
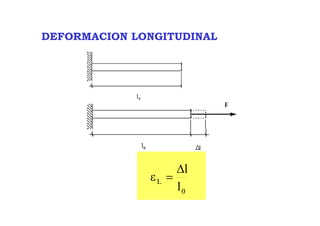
1) El documento describe los conceptos básicos de deformación en sólidos, incluyendo deformaciones longitudinales, angulares y de corte. 2) Explica cómo medir las deformaciones a través del campo de desplazamientos y define el tensor de deformaciones. 3) Discutes las direcciones principales de deformación y las invariantes asociadas.

![( )
PQ
PQQP
limP
x
x
−
=
∗∗
→∆ 0
ε
( )[ ] ( )[ ]PuxQuxxOPOQQP +−+∆+=−= ∗∗∗∗
( ) ( ) uPuQuPQQP ∆=−=−∗∗
( )
P
0x
x
dx
du
x
u
limP ⎟
⎠
⎞
⎜
⎝
⎛
==
→ ∆
∆
ε
∆
∆x
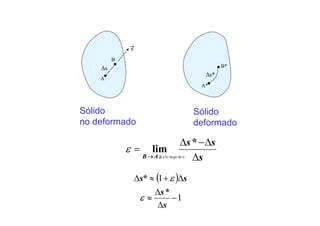
Configuración
sin deformar
Configuración
deformada
x = posición geométrica
u = desplazamiento experimentado](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-4-320.jpg)
![[ ]∗∗∗
→
→
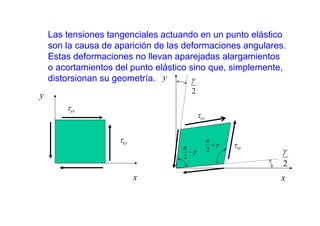
−= RPQánguloQPRánguloγ
PR
PQ
P lim
[ ]∗∗∗
→
→
−= RPQánguloπγ
PR
PQ
P 2
lim
Configuración
sin deformar
Configuración
deformada](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-7-320.jpg)
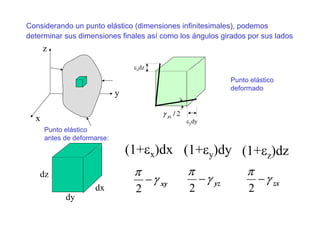

![Relación entre (u’,y’,z’) y (u,v,w):
u' = u +
∂u
∂x
dx +
∂u
∂y
dy +
∂u
∂z
dz
v' = v +
∂v
∂x
dx +
∂v
∂y
dy +
∂v
∂z
dz
w' = w +
∂w
∂x
dx +
∂w
∂y
dy +
∂w
∂z
dz
⎫
⎬
⎪
⎪
⎪
⎭
⎪
⎪
⎪
[ ] rdMPQ
rrr
+δ=δ
[ ]
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
z
w
y
w
x
w
z
v
y
v
x
v
z
u
y
u
x
u
M
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-11-320.jpg)
![[ ]
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
z
w
y
w
x
w
z
v
y
v
x
v
z
u
y
u
x
u
M
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
[ ] [ ]
44444444 344444444 2144444444 344444444 21
simétricaDicahemisimétrW
z
w
z
v
y
w
z
u
x
w
y
w
z
v
y
v
y
u
x
v
x
w
z
u
x
v
y
u
x
u
z
v
y
w
z
u
x
w
y
w
z
v
y
u
x
v
x
w
z
u
x
v
y
u
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+⎟
⎠
⎞
⎜
⎝
⎛
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−⎟
⎠
⎞
⎜
⎝
⎛
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
2
1
2
1
2
1
2
1
2
1
2
1
0
2
1
2
1
2
1
0
2
1
2
1
2
1
0
=
Descomposición de la matriz [M]
P
Q
P*
Q*δQ
δP
d r d r*
[ ] rdMPQ
rrr
+δ=δ
[ ] [ ]( ) rdDWPQ
rrr
++δ=δ
d
r
r∗
= d
r
r +
r
δQ −
r
δP
[ ] [ ] rdDrdWrdrd
rrrr
++=∗
[ ] [ ]( ) [ ] rdDrdWIrd
rrr
++=∗](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-12-320.jpg)
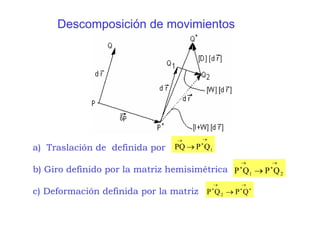
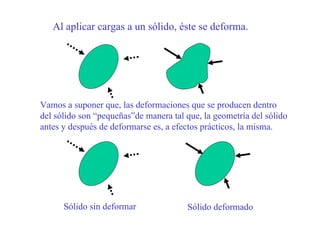
![Los pasos a) y b) son comunes (traslación + giro) para
todos los puntos del entorno del punto P, por lo que no
producen variación relativa alguna (deformación) de las
distancias entre el punto P y dichos puntos. Sólo el paso
c) es el que produce deformaciones en el entorno del
punto P y el tensor correspondiente, que admite una
representación a través de la matriz [D] respecto al
sistema de coordenadas que estamos empleando,
se denomina Tensor de Deformaciones](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-14-320.jpg)
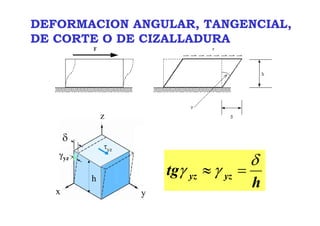
![INTERPRETACION FISICA DE LAS COMPONENTES DEL
TENSOR DE DEFORMACIONES
εx =
∂u
∂x
, εy =
∂v
∂y
, εz =
∂w
∂z
,
γ xy =
∂u
∂y
+
∂v
∂x
, γ xz =
∂u
∂z
+
∂w
∂x
, γyz =
∂v
∂z
+
∂w
∂y
D[ ]=
εx
γ xy
2
γ xz
2
γ xy
2
εy
γ yz
2
γ xz
2
γyz
2
εz
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-15-320.jpg)
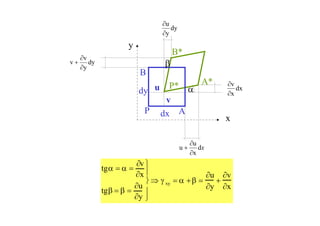
![DEFORMACIONES EN UNA DIRECCION CUALQUIERA
Vector deformación unitaria: ε
r
[ ] [ ] [ ] [ ]uD
dr
rd
D
r
r
limD
r
rD
lim 0r0r
v
rrr
r
==== →→
∆
∆
∆
∆
ε ∆∆
π](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-17-320.jpg)

lnmnlmnml
uuD=u=usobre.proy
xzyzxy
2
z
2
y
2
xn
n
γ+γ+γ+ε+ε+ε=ε
⋅⋅⋅εε=ε
rrrrrr
Deformación angular unitaria:
n /2γ
2
n
2
n
2
4
1
γεε +=
ε
r
Relación:
[ ]uD
vr
=ε](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-18-320.jpg)
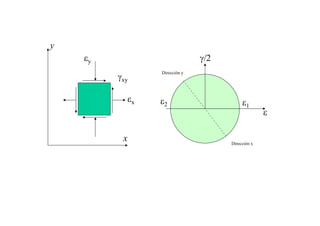
![DIRECCIONES PRINCIPALES E INVARIANTES
¿Para qué direcciones el vector deformación es perpendicular al plano correspondiente?
⇓
=− TICACARACTERISECUACION0ID ε
032
2
1
3
=−+− III εεε
u
yxxyyxxy γγεε
2
1
2
1
===
[ ]
[ ] 0
rr
rr
=−
=
uID
uuD
ε
ε
γxy//2
γxy//2
γxy//2
γxy//2
x
x
yy
Dirección 1
Dirección 2](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-19-320.jpg)

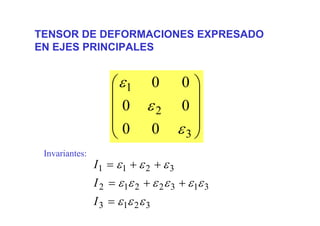
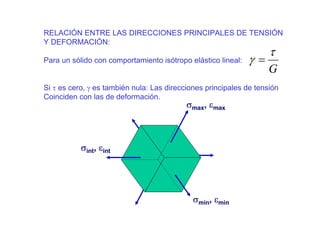

zyxV εεεe ++= = I1
=](https://image.slidesharecdn.com/capitulo2deformacion-150501193634-conversion-gate01/85/Capitulo-2-deformacion-23-320.jpg)