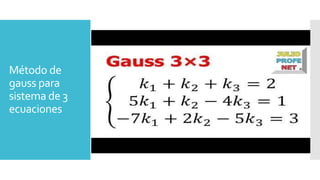
Este documento describe varios métodos para resolver sistemas de ecuaciones lineales, incluyendo el método de Gauss, el método de Gauss-Jordan, el método de descomposición LU, el método de pivoteo y el método de Jacobi. Explica que estos métodos transforman sistemas de ecuaciones en otras formas equivalentes para encontrar sus soluciones numéricamente.

1. RESOLUCIÓN NUMÉRICA
DESISTEMA DE
ECUACIONES LINEALES.
Ingeniería Industrial – Politécnico Santiago Mariño
Francisco J. Alvarado R. v-20408612

2. Introducción
En la siguiente presentación estudiaremos los distintos métodos de resolución
numérica de sistemas de ecuaciones en donde primero definiremos cada uno de ellos y
posteriormente procederemos a resolver problemarios de acuerdo al método aplicado,
de esta manera contaremos con distintas maneras o herramientas por el cual podemos
conseguir solución a un problema matemático de ecuaciones.

3. Isaac Newton fue quien presentó por primera vez el método en su formulación
moderna, aunque no lo quiso publicar. Entre 1650 y 1750 hay 35 fuentes sólo en
Inglaterra en las que aparece descrito el método. La mayoría de los libros de álgebra
del s. XVIII apuntaban que el método fue inventado por Newton (el método de
Newton para la resolución de sistemas de ecuaciones lineales simultáneas). Por
ejemplo, Hammond en su «The elements of algebra,» en 1752, nos presenta «El
método para resolver problemas que contienen cuatro ecuaciones y cuatro
incógnitas» de Newton (The Method of resolving Questions, which contain four
Equations, and four unknown Quantities).
¿Por qué el método de eliminación de incógnitas se popularizó con Gauss? Para
Grcar, todo nuevo método necesita un problema que resolver. Gauss lo utilizó en el
marco del método de mínimos cuadrados, de gran utilidad en la resolución de
múltiples problemas prácticos, como por ejemplo la determinación de la órbitas
astronómicas, Gauss lo aplicó al asteroide Ceres, o en geodesia y cartografía. La
«zorra» de Gauss (que como la zorra borra sus huellas con el rabo) utilizó el método
de eliminación para la resolución de muchísimos problemas, sin indicar los detalles.
¿Por qué? Para qué indicar los detalles si era un método «común» (ampliamente
conocido, según Gauss, claro).
Historia del
método de
gauss

4. Método de
gauss
El método de Gauss consiste en transformar un sistema de ecuaciones en otro
equivalente de forma que este sea escalonado. Para facilitar el cálculo vamos a
transformar el sistema en una matriz, en la que pondremos los coeficientes de
las variables y los términos independientes (separados por una recta)
Dado un sistema AX=bAX=b, el método de eliminación de Gauss consiste en
hallar la forma escalonada de la matriz ampliada del sistema, A∗=(A|b)A∗=(A|b)

5. Método de
gauss para
sistema de 2
ecuaciones

6. Método de
gauss para
sistema de 3
ecuaciones

7. Método de
eliminación
Gauss-Jordan
En matemáticas, la eliminación de Gauss Jordan, llamada así en honor de Carl Friedrich
Gauss y Wilhelm Jordan es un algoritmo del álgebra lineal que se usa para determinar
las soluciones de un sistema de ecuaciones lineales, para encontrar matrices e inversas.
Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus
soluciones mediante la reducción del sistema dado a otro equivalente en el que cada
ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la
matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan
continúa el proceso de transformación hasta obtener una matriz diagonal.

8. Método de
eliminación
Gauss-Jordan

9. Método de
descomposición
LU
En el álgebra lineal, la factorización o descomposición LU (del inglés Lower-Upper) es
una forma de factorización de una matriz como el producto de una matriz triangular
inferior y una superior. Debido a la inestabilidad de este método, deben tenerse en
cuenta algunos casos especiales, por ejemplo, si uno o varios elementos de la diagonal
principal de la matriz a factorizar es cero, es necesario premultiplicar la matriz por una
o varias matrices elementales de permutación. Existe un segundo método llamado
factorización PA=LUPA=LU o LU con pivote. Esta descomposición se usa en el análisis
numérico para resolver sistemas de ecuaciones (más eficientemente) o encontrar las
matrices inversas.

10. Método de
descomposición
LU

11. Método de
descomposición
LU

12. Método de
pivoteo
Con el fin de reducir el error en los procesos concernientes a la eliminación gaussiana,
se ha procurado el estudio hacia los elementos pivotes.
El pivoteo parcial es una de las técnicas de pivoteo. Dicta que el elemento pivote que
debe escogerse es el mayor absolutamente de cada columna.
Así inicialmente, se organiza la matriz para que el elemento absolutamente mayor de la
primera columna sea el primer pivote, luego se realiza la eliminación y a la hora de
pasar al segundo elemento debe considerarse el mayor absolutamente para ubicarlo
como pivote y nuevamente hacer la eliminación, el proceso sigue hasta que ya no
hayan elementos bajo el pivote o hasta que se hayan recorrido todas las columnas de la
matriz. Este método aun teniendo errores de redondeo o de propagación son menores
que los que se presentan en el método de eliminación gaussiana.

13. Método de
pivoteo para
resolución de
problema
matemático.
Método de
pivoteo para
resolución de
problema
matemático.

14. Método de
pivoteo para
resolución de
problema
matemático.

15. Método de
Jacobi
En análisis numérico el método de Jacobi es un método iterativo, usado para resolver
sistemas de ecuaciones lineales del tipo Ax =b El algoritmo toma su nombre del
matemático alemán Carl Gustav Jakob Jacobi. El método de Jacobi consiste en usar
fórmulas como iteración de punto fijo.
La base del método consiste en construir una sucesión convergente definida
iterativamente. El límite de esta sucesión es precisamente la solución del sistema. A
efectos prácticos si el algoritmo se detiene después de un número finito de pasos se
llega a una aproximación al valor de x de la solución del sistema.

16. Método de
Jacobi

17. Método de
Jacobi

18. Conclusión
Los métodos numéricos son técnicas mediante las cuales es posible formular
problemas matemáticos de tal forma que puedan resolverse usando operaciones
aritméticas.
El análisis numérico trata de diseñar métodos para “aproximar” de una manera
eficiente las soluciones de problemas expresados matemáticamente.
El objetivo principal del análisis numérico es encontrar soluciones “aproximadas” a
problemas complejos utilizando sólo las operaciones más simples de la aritmética. Se
requiere de una secuencia de operaciones algebraicas y lógicas que producen la
aproximación al problema matemático.

19. Bibliografía
• Métodos matemáticos (Gauss)
https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales
• Métodos matemáticos (EliminaciónGauss-Jordan)
https://www.matesfacil.com/matrices/resueltos-matrices-SEL-
GAUSS.html
• Métodos matemáticos (Descomposición LU)
https://es.wikipedia.org/wiki/Factorización_LU
• Métodos matemáticos (Pivoteo parcial)
https://sites.google.com/site/procesosnumericosg20141/.../metodo-
de-pivoteo-parcial
• Teoremas matemáticos (Jacobi)
https://es.wikipedia.org/wiki/Método_de_Jacobi