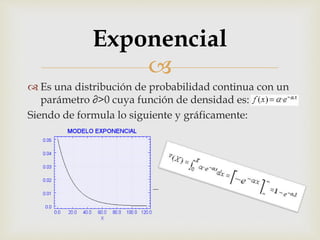
Este documento introduce conceptos básicos de estadística como variables aleatorias discretas y continuas, función de distribución de probabilidad, esperanza matemática, varianza y desviación estándar. Luego describe distribuciones de probabilidad discretas como Bernoulli, binomial, geométrica y Poisson, así como distribuciones continuas como uniforme, exponencial y normal. Finalmente concluye que la estadística se divide en descriptiva e inferencial para analizar y resumir datos de poblaciones y muestras.

1. 
REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL P.P PARA LA EDUCACIÓN SUPERIOR
INSTITUTO UNIVERSITARIO POLITÉCNICO
“SANTIAGO MARIÑO”
BARCELONA – EDO. ANZOÁTEGUI
INGENIERIA DE SISTEMAS (47)
ESTADISTICA II
Br: Ramírez S Luis J
C.I: 19.184.275

2. ESTADISTICA II
PRESENTACION I

3. 
La Estadística es una disciplina que utiliza recursos
matemáticos para organizar y resumir una gran
cantidad de datos obtenidos de la realidad, e inferir
conclusiones respecto de ellos. Aplicada a la
investigación científica, también infiere cuando provee
los medios matemáticos para establecer si
una hipótesis debe o no ser rechazada.
Introducción

4. 
Definición de variables aleatorias
discretas y continuas
Una variable aleatoria: Es una variable
estadística cuyos valores se obtienen de
mediciones en algún tipo de experimento
aleatorio. Formalmente, una variable aleatoria
es una función, que asigna eventos. Por
ejemplo, lanzar un dado o una moneda.

5. 
Variables aleatorias continuas
 Definición:
El conjunto de posibles
valores es numerable.
Suelen estar asociadas a
experimentos en que se
mide el número de veces
que sucede algo.
El conjunto de posibles valores
es no numerable. Puede tomar
todos los valores de un
intervalo. Son el resultado de
medir.

6. Función de distribución de probabilidades
acumuladas. Esperanza matemática, valor
esperado, varianza y desviación estándar,
función generadora de momentos.

7. 
Función de distribución de
probabilidades acumuladas
 La función de
distribución (acumulada)
de una variable
aleatoria X, evaluada
en x, es la probabilidad de
que X tome un valor
menor o igual que x. La
palabra 'acumulada' es
redundante y se puede
omitir.

8. 
Esperanza matemática
Es igual al sumatorio de
las probabilidades de que
exista un suceso aleatorio,
multiplicado por el valor
del suceso aleatorio. O,
dicho de otra forma, el
valor medio de un
conjunto de datos.
También llamado
Valor Esperado

9. 
Valor esperado
Es llamado igual que
Esperanza Matemática, su
definición y aplicación es
el mismo, su formulación
es aplicable para una
probabilidad esperada

10. 
Varianza y desviación estándar
 Desviación Estándar:
La desviación estándar (σ)
mide cuánto se separan
los datos.
La fórmula es fácil: Es la
raíz cuadrada de
la varianza. Así que, "¿qué
es la varianza?"
 Varianza:
La varianza (que es el
cuadrado de la desviación
estándar: σ2) se define así:
Es la media de las
diferencias con la
media elevadas al
cuadrado.

11. 
Explicación en 3 pasos
1. Calcula la media (el promedio de los números)
2. Ahora, por cada número resta la media y eleva el
resultado al cuadrado (la diferencia elevada al
cuadrado).
3. Ahora calcula la media de esas diferencias al
cuadrado.
Explicación Varianza y desviación
estándar

12. 
 En probabilidad y estadística, la función generadora
de momentos o función generatriz de momentos de
una variable aleatoria X es:
Siempre que esta esperanza exista.
 La función generadora de momentos se llama así
porque, si existe en un entorno de t = 0, permite
generar los momentos de la distribución de
probabilidad
Función generadora de momentos.

13. 
 Si X es una variable aleatoria discreta
 Si la variable es continua
Puede demostrarse que si la función generadora de
momentos existe, entonces es única y determina por
completo a la distribución de probabilidad de X. Es decir, si
dos variables aleatorias tienen la misma función generatriz
de momentos, entonces, las dos variables tienen también la
misma distribución de probabilidad.
Función generadora de momentos

14. Distribuciones discretas de probabilidad:
Bernoulli, Binomial, Geométrica, Binomial
negativa, Multinomial, Poisson,
Hipergeométrica, Poisson como aproximación
a la binomial e hipergeométrica.

15. 
 La distribución de Bernoulli (o distribución
dicotómica) Es una distribución de
probabilidad discreta, que toma valor 1 para la
probabilidad de éxito (p) y valor 0 para la
probabilidad de fracaso (q = 1 - p).
 Si X es una variable aleatoria que mide "número de
éxitos", y se realiza un único experimento con dos
posibles resultados (éxito o fracaso), se dice que la
variable aleatoria X se distribuye como una Bernoulli
de parámetro P.
Bernoulli

16. 
Es una distribución de probabilidad discreta que mide
el número de éxitos en una secuencia de n ensayos
de Bernoulli independientes entre sí, con una
Probabilidad fija p de ocurrencia del éxito entre los
ensayos.
se trata de calcular la probabilidad de un determinado
número de éxitos. Para N = 1, la Binomial se convierte,
de hecho, en una distribución de Bernoulli.
Binomial

17. 
 Es cualquiera de las dos distribuciones de
probabilidad discretas siguientes:
la distribución de probabilidad del
número X del ensayo de Bernoulli necesaria para
obtener un éxito, contenido en el conjunto { 1, 2, 3,...} Ó
la distribución de probabilidad del número Y = X − 1 de
fallos antes del primer éxito, contenido en el conjunto {
0, 1, 2, 3,... }.
Geométrica

18. 
 Es un modelo adecuado para tratar aquellos
procesos en los que se repite un determinado ensayo
o prueba hasta conseguir un número determinado de
resultados favorables (por vez primera), puede
considerarse una ampliación o extensión de la
distribución geométrica.
Binomial Negativa

19. 
 Este modelo se puede ver como una generalización
del Binomial en el que, en lugar de tener dos posibles
resultados, tenemos r resultados posibles.
 Si repetimos la experiencia n veces en condiciones
independientes, podemos preguntarnos la
probabilidad de que el suceso A1 aparezca k1 veces, el
suceso A2, k2 veces y así sucesivamente:
Multinomial

20. 
Multinomial
 Al modelo estadístico
que nos da dicha
probabilidad se le
denomina Multinomial,
y su función de
densidad viene dada
por:

21. 
 Es una distribución de probabilidad discreta que
expresa, a partir de una frecuencia de ocurrencia
media, la probabilidad de que ocurra un
determinado número de eventos durante cierto
período de tiempo.
Poisson

22. 
 es una distribución discreta relacionada
con muestreos aleatorios y sin reemplazo. Suponga
que se tiene una población de N elementos de los
cuales, d pertenecen a la categoría A y N-d a la B. La
distribución hipergeométrica mide la probabilidad
de obtener x (0 ≤ 𝑥 ≤ 𝑑) elementos de la
categoría A en una muestra sin reemplazo
de n elementos de la población original.
Hipergeometrica

23. 
 Se puede demostrar que una binomial cuya n (número de
experimentos) es muy grande y su p (probabilidad)
tiende a 0, es decir, un suceso raro. Se aproxima como una
Poisson con λ=n•p
 La diferencia entre las distribuciones hipergeométrica y
binomial radica en que la probabilidad de éxito es
variable en la primera y constante en la segunda. Una
forma de convertir un experimento de probabilidad
variable a probabilidad constante es realizarlo sin
reposición, para el primer caso, y con reposición en el
segundo caso.
Poisson como aproximación a la
binomial e hipergeométrica

24. 
Uniforme
Exponencial
Gamma
Beta
Weibull
Normal estandarizada y normal como aproximación a
la binomial.
Distribuciones continuas de
Probabilidades

25. 
 Es el modelo (absolutamente) continuo más simple.
Corresponde al caso de una variable aleatoria que
sólo puede tomar valores comprendidos entre dos
extremos a y b, de manera que todos los intervalos
de una misma longitud (dentro de (a, b)) tienen la
misma probabilidad.
Uniforme

26. 
 Es una distribución de probabilidad continua con un
parámetro ∂>0 cuya función de densidad es:
Siendo de formula lo siguiente y gráficamente:
Exponencial

27. 
Si x1,...,xn son n variables aleatorias independientes
distribuidas según una N(0,1).
La nueva variable aleatoria Y= x2
1,...,x2
n
sigue una distribución (n/2,1/2)
Cuando el parámetro p es entero, a la distribución
(p,a) se le conoce con el nombre de distribución Erlang
Gamma

28. 
 Suele utilizarse para modelar la distribución de
estadísticos de orden (por ejemplo, el estadístico de
orden késimo de una muestra de variables n uniformes
(0, 1) tiene una distribución beta (k, n + 1 – k)) y para
modelar eventos que se definen por valores mínimos
y máximos.
Beta

29. 
Es una distribución versátil que se puede utilizar para
modelar una amplia gama de aplicaciones en
ingeniería, investigación médica, control de calidad,
finanzas y climatología. Por ejemplo, la distribución se
utiliza frecuentemente con análisis de fiabilidad para
modelar datos de tiempo antes de falla.
Weibull

30. 
 En este caso se estarán calculando probabilidades
de experimentos Binomiales de una forma muy
aproximada con la distribución Normal, esto puede
llevarse a cabo si n¥® y p = p(éxito) no es muy
cercana a 0 y 1, o cuando n es pequeño y p tiene un
valor muy cercano a ½ ; esto es,
Normal estandarizada y normal como
aproximación a la binomial.

31. 
La distribución normal estándar, o tipificada o
reducida, es aquella que tiene por media el
valor cero, μ = 0, y por desviación típica la unidad, σ
=1.
Su función de densidad es

32. 
 La Estadística es una ciencia matemática que se utiliza para
describir, analizar e interpretar ciertas características de un
conjunto de individuos llamado población. Cuando nos
referimos a muestra y población hablamos de conceptos
relativos pero estrechamente ligados. Una población es un todo
y una muestra es una fracción o segmento de ese todo.
 Podemos dividir la estadística en dos ramas; la estadística
descriptiva, que se dedica a los métodos de
recolección, descripción, visualización y resumen de datos
originados a partir de los fenómenos en estudio; y la estadística
inferencial, que se dedica a la generación de los modelos,
inferencias y predicciones asociadas a los fenómenos en
cuestión.
Conclusiones