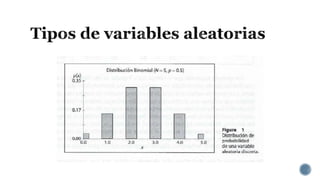
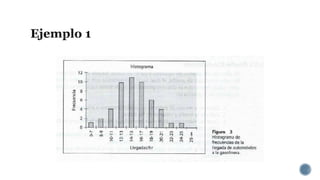
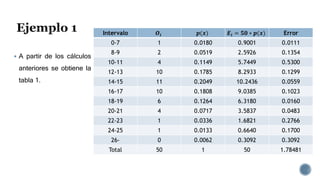
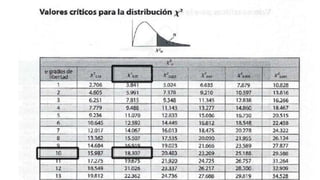
Este documento describe las variables aleatorias y sus distribuciones de probabilidad para la creación de modelos de simulación. Explica que las variables aleatorias pueden ser discretas o continuas y deben cumplir con reglas de distribución. También describe distribuciones comunes como la binomial, Poisson, normal y cómo determinar la distribución de datos históricos usando pruebas estadísticas.

1. Clase 2

2.  Hemos mencionado que un modelo de simulación permite lograr un mejor entendimiento
de prácticamente cualquier sistema.
 Para ello resulta indispensable obtener la mejor aproximación a la realidad, lo cual se
consigue componiendo el modelo a base de variables aleatorias que interactúen entre sí.
 Pero, ¿cómo podemos determinar qué tipo de distribución tiene una variable aleatoria?
¿Cómo podemos usarla en el modelo, una vez que conocemos su distribución asociada?
Comentaremos los métodos y herramientas que pueden dar contestación a estas
interrogantes clave para la generación del modelo.

3.  Podemos decir que las variables aleatorias son aquellas que tienen un
comportamiento probabilístico en la realidad.
 Por ejemplo, el número de clientes que llegan cada hora a un banco depende del
momento del día, del día de la semana y de otros factores: por lo general, la afluencia
de clientes será mayor al mediodía que muy temprano por la mañana; la demanda
será más alta el viernes que el miércoles; habrá más clientes un día de pago que un
día normal, etc.

4.  Dadas estas características, las variables aleatorias deben cumplir reglas de
distribución de probabilidad como éstas:
 La suma de las probabilidades asociadas a todos los valores posibles de la variable aleatoria
𝑥 es uno.
 La probabilidad de que un posible valor de la variables 𝑥 se presente siempre es mayor que
o igual a cero.
 El valor esperado de la distribución de la variable aleatoria es la media de la misma, la cual a
su vez estima la verdadera media de la población.

5.  Si la distribución de probabilidad asociada a una variable aleatoria está definida por más de
un parámetro, dichos parámetros pueden obtenerse mediante un estimador no sesgado. Por
ejemplo, la varianza de la población 𝜎2 puede ser estimada usando la varianza de una
muestra que es 𝑠2
. De la misma manera, la desviación estándar de la población, 𝜎, puede
estimarse mediante la desviación estándar de la muestra 𝑠.

6.  Podemos diferenciar las variables aleatorias de acuerdo con el tipo de valores aleatorios que
representan.
 Por ejemplo, si habláramos del número de clientes que solicitan cierto servicio en un periodo de
tiempo determinado, podríamos encontrar valores tales como 0,1,2, . . , 𝑛, es decir, un comportamiento
como el que presentan las distribuciones de probabilidad discretas.
 Por otro lado, si habláramos del tiempo que tarda en ser atendida una persona, nuestra investigación
tal vez arrojaría resultados como 1.54 minutos, 0.028 horas o 1.37 días, es decir, un comportamiento
similar al de las distribuciones de probabilidad continuas. Considerando lo anterior podemos
diferenciar entre variables aleatorias discretas y variables aleatorias continuas.

7.  Variables aleatorias discretas. Este tipo de variables deben cumplir con estos
parámetros:
 𝑃 𝑥 ≥ 0
 𝑖=0
∞
𝑝𝑖 = 1
 𝑃 𝑎 ≤ 𝑥 ≤ 𝑏 = 𝑖=0
𝑏
𝑝𝑖 = 𝑝 𝑎 + ⋯ + 𝑝 𝑏

8.  Algunas distribuciones discretas de probabilidad son la uniforme discreta, la de
Bernoulli, la hipergeométrica, la de Poisson y la binomial (vea la figura 1).
 Podemos asociar a estas u otras distribuciones de probabilidad el comportamiento de
una variable aleatoria.
 Por ejemplo, si nuestro propósito al analizar un muestreo de calidad consiste en
decidir si la pieza bajo inspección es buena o no, estamos realizando un experimento
con dos posibles resultados: la pieza es buena o la pieza es mala.

10.  Este tipo de comportamiento está asociado a una distribución de Bernoulli. Por otro
lado, si lo que queremos es modelar el número de usuarios que llamarán a un
teléfono de atención a clientes, el tipo de comportamiento puede llegar a parecerse a
una distribución de Poisson.
 Incluso podría ocurrir que el comportamiento de la variable no se pareciera a otras
distribuciones de probabilidad conocidas.

11.  Si éste fuera el caso, es perfectamente válido usar una distribución empírica que se
ajuste a las condiciones reales de probabilidad.
 Esta distribución puede ser una ecuación o una suma de términos que cumplan con
las condiciones necesarias para ser consideradas una distribución de probabilidad.

12.  Variables aleatorias continuas. Este tipo de variables se representan mediante una
ecuación que se conoce como función de densidad de probabilidad. Dada esta
condición, cambiamos el uso de la sumatoria por la de una integral para conocer la
función acumulada de la variable aleatoria.

13.  Por lo tanto, las variables aleatorias continuas deben cumplir los siguientes
parámetros:
 𝑃 𝑥 ≥ 0
 −∞
∞
𝑓 𝑥 = 1
 𝑃 𝑎 ≤ 𝑥 ≤ 𝑏 = 𝑃 𝑎 < 𝑥 < 𝑏 = 𝐹 𝑥 = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥

14.  Entre las distribuciones de probabilidad tenemos la uniforme continua, la exponencial,
la normal, la de Weibull, la Chi-cuadrada y la de Erlang (vea la figura 2). Al igual que
en el caso de las distribuciones discretas, algunos procesos pueden ser asociados a
ciertas distribuciones.

16.  Entre las distribuciones de probabilidad tenemos la uniforme continua, la exponencial,
la normal, la de Weibull, la Chi-cuadrada y la de Erlang (vea la figura 2). Al igual que
en el caso de las distribuciones discretas, algunos procesos pueden ser asociados a
ciertas distribuciones.

17.  Por ejemplo, es posible que el tiempo de llegada de cada cliente a un sistema tenga
una distribución de probabilidad muy semejante a una exponencial, o que el tiempo
que le toma a un operario realizar una serie de tareas se comporte de manera muy
similar a la dispersión que presenta una distribución normal.

18.  Sin embargo, debemos hacer notar que este tipo de distribuciones tienen sus
desventajas, dado que el rango de valores posibles implica que existe la posibilidad
de tener tiempos infinitos de llegada de clientes o tiempos de ensamble infinitos,
situaciones lejanas a la realidad.
 Por fortuna, es muy poco probable de se presenten este tipo de eventos, aunque el
analista de la simulación debe estar consciente de cómo pueden impactar valores
como los descritos en los resultados del modelo. Posteriormente revisaremos algunas
herramientas útiles para lograr ese objetivo.

19.  La distribución de probabilidad de los datos históricos puede determinarse mediante
las pruebas Chi-cuadrada, de Kolmogorov-Smirnov y de Anderson-Darling.
Revisaremos los procedimientos de cada una de estas pruebas, así como la forma de
realizarlas a través de Stat: :Fit, una herramienta complementaria de ProModel.

20.  Se trata de una prueba de hipótesis a partir de datos, basada en el cálculo de un valor
llamado estadístico de prueba, al cual suele comparársele con un valor conocido
como valor crítico, mismo que se obtiene, generalmente, de tablas estadísticas.

21.  El procedimiento general de la prueba es:
 Obtener al menos 30 datos de la variable aleatoria a analizar.
 Calcular la media y varianza de los datos.
 Crear un histograma de 𝑚 = 𝑥 intervalos, y obtener la frecuencia observada en cada
intervalo 𝑂𝑖
 Establecer explícitamente la hipótesis nula, proponiendo una distribución de probabilidad
que se ajuste a la forma del histograma.
 Calcular la frecuencia esperada, 𝐸𝑖, a partir de la función de probabilidad propuesta.

22.  El procedimiento general de la prueba es:
 Calcular el estadístico de prueba:
 𝑋 𝑜
2
= 𝑖=1
𝑚 𝐸 𝑖−𝑂𝑖
2
𝐸𝑖
 Definir el nivel de significancia de la prueba, 𝛼, y determinar el valor crítico de la prueba,
𝑋 𝛼,𝑚−𝑘−1
2
( 𝑘 es el número de parámetros estimados en la distribución propuesta).
 Comparar el estadístico de prueba con el valor crítico. Si el estadístico de prueba es menor
que el valor crítico no se puede rechazar la hipótesis nula.

23.  Éstos son los datos del número de automóviles que entran a una gasolinera cada
hora:

24.  Determinar la distribución de probabilidad con un nivel de significancia 𝛼 de 5 %
(0.05).
 El histograma (vea la figura 3) de los n = 50 datos, considerando m = 11 intervalos, la
media muestral de 15.04 y la varianza muestral de 13.14, permiten establecer la
siguiente hipótesis:
 𝐻 𝑜: Poisson (A = 15) automóviles/hora Hy Otra distribución
 𝐻1: Otra distribución

26.  Comenzamos por calcular la probabilidad de cada intervalo a partir de la función de
 probabilidad de Poisson:
 𝑝 𝑥 =
𝜆 𝑥 𝑒−𝜆
𝑥!
, 𝑥 = 0,1,2, … . .
 𝑝 𝑥 =
15 𝑥 𝑒−15
𝑥!
, 𝑥 = 0,1,2, … . .
 Por ejemplo, para el intervalo 8-9
 𝑝 𝑥 = 8,9 =
158 𝑒−15
8!
+
159 𝑒−15
9!
= 0.0519

27.  Comenzamos por calcular la probabilidad de cada intervalo a partir de la función de
 probabilidad de Poisson:
 𝑝 𝑥 =
𝜆 𝑥 𝑒−𝜆
𝑥!
, 𝑥 = 0,1,2, … . .
 𝑝 𝑥 =
15 𝑥 𝑒−15
𝑥!
, 𝑥 = 0,1,2, … . .
 Por ejemplo, para el intervalo 8-9
 𝑝 𝑥 = 8,9 =
158 𝑒−15
8!
+
159 𝑒−15
9!
= 0.0519

28.  Enseguida calculamos la frecuencia esperada en cada intervalo, multiplicando la
probabilidad 𝑝(𝑥) por el total de datos de la muestra:
 𝐸𝑖 𝑥 = 𝑛𝑝(𝑥)
 𝐸𝑖 = 50𝑝(𝑥)
 Y luego estimamos el estadístico de la prueba:
 𝑐 = 𝑋 𝑜
2 = 𝑖=1
𝑚 𝐸 𝑖−𝑂 𝑖
2
𝐸 𝑖
=
0.9001−1 2
0.9001
+
2.5926−2 2
2.5926
+ ⋯ +
0.3092−0 2
0.3092
= 1.7848

29.  A partir de los cálculos
anteriores se obtiene la
tabla 1.
Intervalo 𝑶𝒊 𝒑(𝒙) 𝑬𝒊 = 𝟓𝟎 ∗ 𝒑(𝒙) Error
0-7 1 0.0180 0.9001 0.0111
8-9 2 0.0519 2.5926 0.1354
10-11 4 0.1149 5.7449 0.5300
12-13 10 0.1785 8.2933 0.1299
14-15 11 0.2049 10.2436 0.0559
16-17 10 0.1808 9.0385 0.1023
18-19 6 0.1264 6.3180 0.0160
20-21 4 0.0717 3.5837 0.0483
22-23 1 0.0336 1.6821 0.2766
24-25 1 0.0133 0.6640 0.1700
26- 0 0.0062 0.3092 0.3092
Total 50 1 50 1.78481

30.  El valor del estadístico de prueba,𝑋 𝑜
2 = 1.7848, comparado con el valor de tablas
crítico,𝑋0.05,11−0−1
2
= 18.307, indica que no podemos rechazar la hipótesis de que la
variable aleatoria se comporta de acuerdo con una distribución de Poisson, con una
media de 15 automóviles/hora.

32.  Checar la practica 1 anexo de la Teoría