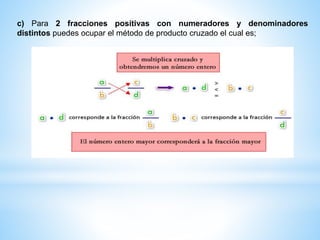
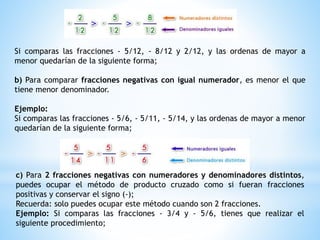
Este documento proporciona instrucciones para comparar diferentes tipos de números racionales como fracciones y decimales. Explica métodos como usar el producto cruzado para dos fracciones o igualar denominadores para varias fracciones. También cubre cómo comparar números decimales cifra por cifra y números racionales mixtos transformándolos a la misma forma.

1. *
¿Te han planteado un problema parecido y no sabes cómo
resolverlo? ¡No te preocupes! A continuación te daremos las
claves para que puedas resolverlos con mucha facilidad.
Repasemos los diferentes métodos para comparar
fracciones y números decimales ya estudiados, esta vez con
una mayor cantidad de números.

2. 1.1- Comparación de fracciones positivas
Para comparar fracciones positivas puedes utilizar los siguientes métodos;
a) Para comparar fracciones positivas con igual denominador, es menor la
que tiene menor numerador.
Ejemplo: Si comparas las fracciones 5/9, 2/9 y 4/9, y las ordenas de mayor a
menor quedarían de la siguiente forma;
b) Para comparar fracciones positivas con igual numerador, es menor el que
tiene mayor denominador.
Ejemplo: Si comparas las fracciones 3/8, 3/7, 3/13, 3/5, y las ordenas de mayor a
menor quedarían de la siguiente forma;

3. c) Para 2 fracciones positivas con numeradores y denominadores
distintos puedes ocupar el método de producto cruzado el cual es;

4. Recuerda: solo puedes ocupar este método cuando son 2 fracciones.
Ejemplo: Si comparamos las fracciones 7/10 y 4/5, realizamos el siguiente
procedimiento;
Respuesta: 7/10 es menor que 4/5.
d) Para comparar varias fracciones positivas con numeradores y
denominadores distintos, puedes seguir los siguientes pasos:
1° Anota las fracciones dadas.
2° Calcula el mínimo común múltiplo de los denominadores.
3° Iguala las fracciones dadas.
4° Ordena las fracciones según lo solicitado en el problema.
5° Escribe las fracciones originales según lo solicitado.
Ejemplo:
Ordena de mayor a menor las siguientes fracciones; 5/3, 1/4, 7/2 y 3/11.

6. - Entonces, para comparar las fracciones 5/3, 1/4, 7/2 y 3/11, y poder
ordenarlas de mayor a menor, calculamos el mínimo común múltiplo entre los
denominadores, que es 132 y amplificamos cada una de las fracciones para que
tengan el mismo denominador, luego comparamos sus numeradores y las
ordenamos.
1.2- Comparación de fracciones negativas
Para comparar fracciones negativas puedes ocupar los mismos métodos que en
el caso de las fracciones positivas, teniendo encuentra que, cuando comparas
fracciones negativas, cuanto mayor sea la fracción menor será el valor, esto es
porque la fracción menor negativa es la que está más cerca del cero, si lo
piensas la regla es al revés que para las fracciones positivas, mira la siguiente
regla numérica para que lo entiendas mejor;
Ejemplo:
En esta regla numérica la fracción menor es la fracción – 3/5
Entonces;
a) Para comparar fracciones negativas con igual denominador, es menor la que
tiene mayor numerador.
Ejemplo:

7. Si comparas las fracciones - 5/12, - 8/12 y 2/12, y las ordenas de mayor a
menor quedarían de la siguiente forma;
b) Para comparar fracciones negativas con igual numerador, es menor el que
tiene menor denominador.
Ejemplo:
Si comparas las fracciones - 5/6, - 5/11, - 5/14, y las ordenas de mayor a menor
quedarían de la siguiente forma;
c) Para 2 fracciones negativas con numeradores y denominadores distintos,
puedes ocupar el método de producto cruzado como si fueran fracciones
positivas y conservar el signo (-);
Recuerda: solo puedes ocupar este método cuando son 2 fracciones.
Ejemplo: Si comparas las fracciones - 3/4 y - 5/6, tienes que realizar el
siguiente procedimiento;

8. Respuesta: -3/4 es mayor que - 5/6.

9. d) Para comparar varias fracciones negativas con numeradores y
denominadores distintos, puedes seguir mismos pasos que aprendiste para
comparar las fracciones positivas, reservando el signo negativo (-) y
agregándolo después de igualar las fracciones.
1° Anota las fracciones dadas.
2° Calcula el mínimo común múltiplo de los denominadores.
3° Iguala las fracciones dadas y agrega el signo negativo (-).
4° Ordena las fracciones según lo solicitado en el problema.
5° Escribe las fracciones originales según lo solicitado.
Ejemplo:
Ordena de mayor a menor las siguientes fracciones; - 2/3, - 1/6 y - 7/18.

10. 1.3- Comparación de números decimales
Para comparar números decimales debes fijarte en las cifras siempre
de izquierda a derecha, o sea, primero la parte entera y luego los
decimales, cifra a cifra, décimas, centésimas, milésimas… hasta que
encuentres una cifra diferente.
Ejemplo: Si comparas 14,007 y 14,07, ¿Cuál es mayor?

11. Respuesta: 14,07 es mayor que 14,007.
Nota: Para que sea más fácil comparar los números decimales, puedes unir con
una línea las diferentes cifras, como se muestra en el ejemplo.
En el caso de que los números decimales que tengas que comparar sean
decimales infinitos periódicos o semiperiódicos debes escribir los números con
todos sus decimales, y así cifra a cifra poder compararlos, igual que lo
explicado anteriormente.
Ejemplo:

12. Para los números decimales negativos puedes realizar el mismo
procedimiento pero recordando que el número decimal negativo menor es
el que se encuentra más cerca del cero, por lo tanto tiene mayor valor.
Ejemplo: Si comparas -31,22 y -31,12 ¿Cuál es mayor?

13. Respuesta: -31,12 es mayor que -31,22.
2- Comparación de diferentes números racionales
Ahora que ya sabes cómo comparar fracciones y decimales por separado te
darás cuenta lo fácil que es resolver los ejercicios que tengan diferentes
números racionales.
Para comparar números enteros, decimales o fracciones, simplemente puedes
transformar (como aprendiste en el tema anterior) los números decimales a
fracción e igualar sus denominadores y luego comparar, o bien transformar las
fracciones a decimales y luego comparar.
- Ahora resolvamos el ejercicio que planteamos al comienzo; Compara los
siguientes números racionales y ordénalos de menor a mayor.

14. Para comparar y ordenar estos números racionales puedes transformar las
fracciones a decimal o bien transformar los decimales en una fracción. Te
mostraremos estas 2 opciones para el mismo ejercicio.
a) Transformar las fracciones a números a decimales.
*Recuerda que para transformar las fracciones a números decimales
simplemente tienes que dividir el numerador por el denominador.
- Ahora que ya se encuentran todos los números en forma decimal, los
puedes comparar y ordenar.
- Ya que, el problema te solicita ordenar de menor a mayor, compara
primero los números negativos y luego los positivos que no tienen parte
entera y por último los que tienen parte entera y decimales.

15. - Entonces los números decimales quedarían en el siguiente orden de
menor a mayor;
- Por último anotas los números racionales originales en orden de menor a
mayor;

16. b) Transformar los números decimales a fracción.
- Anota las fracciones dadas y transforma los decimales a fracción común,
ocupando los métodos que ya aprendiste en el tema anterior;
- Ya tienes todos los números expresados en fracción ahora, las puedes
comparar, puedes empezar por los números negativos que sólo son 2, en
este caso ocuparemos el método de producto cruzado, recuerda conservar
el signo negativo (-).

17. - Ahora compara las fracciones positivas, en este caso como son varias
fracciones con diferente denominador y numerador, igualaremos sus
denominadores;

19. - Después de igualar el denominador puedes comparar las fracciones y
ordenarlas de menor a mayor, anotando los números racionales originales;