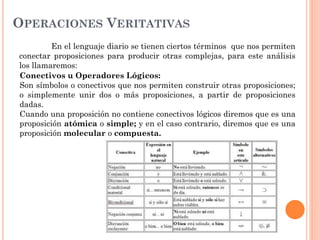
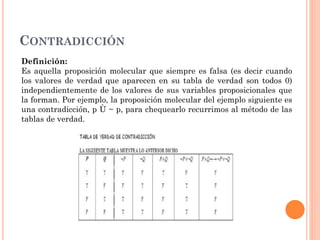
Este documento presenta los conceptos básicos del cálculo proposicional. Define proposiciones, operaciones veritativas como la negación, conjunción, disyunción inclusiva y exclusiva, y el condicional. Explica las tablas de verdad y cómo determinar si una proposición es una tautología o contradicción. También describe las leyes del álgebra proposicional y diferentes métodos de demostración como la directa, indirecta, y reducción al absurdo. El documento concluye resaltando la importancia del cálculo

1. REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACION UNIVERSITARIA
UNIVERSIDAD FERMIN TORO
SISTEMA DE APRENDIZAJES INTERACTIVOS A DISTANCIA
CALCULO PROPOSICIONAL
Barquisimeto-Mayo 2014
Alumna: Hilgri Peraza
C.I.: 10.846.959
Asignatura: Estructuras Discretas

2. PROPOSICIONES
Concepto:
Es un juicio declarativo del cual tiene sentido decir que es verdadero (V) o que es falso (F),
pero no ambas cosas simultaneas. Por ello solo admite una sola alternativa:
 Verdadero:1
 Falso:0
Notación: Las proposiciones se notarán con letras minúsculas p, q, r, s, t, ya que las
letras mayúsculas serán usadas para denotar los conjuntos.

3. OPERACIONES VERITATIVAS
En el lenguaje diario se tienen ciertos términos que nos permiten
conectar proposiciones para producir otras complejas, para este análisis
los llamaremos:
Conectivos u Operadores Lógicos:
Son símbolos o conectivos que nos permiten construir otras proposiciones;
o simplemente unir dos o más proposiciones, a partir de proposiciones
dadas.
Cuando una proposición no contiene conectivos lógicos diremos que es una
proposición atómica o simple; y en el caso contrario, diremos que es una
proposición molecular o compuesta.

4. LA NEGACIÓN
Sea p una proposición, la negación de p es otra proposición
identificada por: ~ p, que se lee "no p", "no es cierto que p", "es
falso que p", y cuyo valor lógico está dado por la negación de
dicha proposición.
La tabla anterior dice, que ~ p es falsa cuando p es verdadera y
que ~ p es verdadera cuando p es falsa.

5. LA CONJUNCIÓN
Definición:
Sean p y q dos proposiciones. La conjunción de p y q es la proposición p Ù
q, que se lee "p y q", y cuyo valor lógico está dado con la tabla o igualdad
siguiente:
VL(p^q) = min (VL(p), VL(q)) en otras palabras el menor valor
de los números dados.

6. DISYUNCIÓN INCLUSIVA
Definición:
Sean p y q dos proposiciones. La disyunción de p y q es la proposición p
v q, que se lee "p o q", y cuyo valor lógico está dado por la tabla
siguiente:
VL(pvq)=máximo valor(VL(p),VL(q)).

7. DISYUNCIÓN EXCLUSIVA
Definición:
Sean p y q dos proposiciones. La disyunción exclusiva de p y q es la
proposición p vq, que se lee "o p o q", y cuyo valor lógico está dado por la
tabla. En otras palabras, la disyunción exclusiva es falsa sólo cuando los
valores de p y q son iguales.
VL(pv q) = 0 si VL (p) = VL ( q ).

8. EL CONDICIONAL
Definición:
Sean p y q dos proposiciones. El condicional con antecedente p y
consecuente q es la proposición p ® q, que se lee "si p, entonces q", y
cuyo valor lógico está dado por la siguiente tabla:
Condición Necesaria y Condición Suficiente
El condicional es una de las proposiciones más importantes en la
matemática, ya que la mayoría de teoremas vienen dados en esa
forma. En los teoremas, el antecedente es llamado hipótesis y el
consecuente tesis. Un condicional puede ser expresado también
con las llamadas condiciones necesarias y suficientes. El
antecedente es la condición suficiente y el consecuente la condición
necesaria.

9. EL BICONDICIONAL
Definición:
Sean p y q dos proposiciones, Se llama Bicondicional de p y q a la
proposición p « q, que se lee "p si sólo si q", o "p es condición necesaria y
suficiente para q", y cuyo valor lógico es dado por la siguiente tabla.
o en otras palabras el VL (P « q ) = 1 si VL (p) = VL (q)
La tabla nos dice que p « q es verdadero cuando VL(p) = VL(q), y
esa falsa cuando VL(p) ¹ VL(q)

10. TABLAS DE VERDAD DE LAS FORMAS
PROPOSICIONALES
Las tablas de verdad permiten determinar el valor de verdad de
una proposición compuesta y depende de las proposiciones simples y de los
operadores que contengan.
Es posible que no se conozca un valor de verdad específico para
cada proposición; es este caso es necesario elaborar una tabla de verdad que
nos indique todas las diferentes combinaciones de valores de verdad que
pueden presentarse. Las posibilidades de combinar valores de verdad
dependen del número de proposiciones dadas, de esta manera:
Para una proposición (n = 1), tenemos 21 = 2 combinaciones
Para dos proposiciones (n = 2), tenemos 22 = 4 combinaciones
Para tres proposiciones (n = 3), tenemos 2 3 = 8 combinaciones
Para n proposiciones tenemos 2n combinaciones

11. TAUTOLOGÍAS Y CONTRADICCIONES
Proposición Tautológica o Tautología
Definición: Es aquella proposición molecular que es verdadera (es decir, todos los
valores de verdad que aparecen en su tabla de verdad son 1) independientemente de
los valores de sus variables.
Ejemplo: Probar que P Ú ~ P es una tautología

12. CONTRADICCIÓN
Definición:
Es aquella proposición molecular que siempre es falsa (es decir cuando
los valores de verdad que aparecen en su tabla de verdad son todos 0)
independientemente de los valores de sus variables proposicionales que
la forman. Por ejemplo, la proposición molecular del ejemplo siguiente es
una contradicción, p Ù ~ p, para chequearlo recurrimos al método de las
tablas de verdad.

13. LEYES DEL ALGEBRA DE PROPOSICIONES
1. Leyes Idempotentes
1.1. p p  p
1.2. p p  p
2. Leyes Asociativas
2.1. (P  q)  r  p  (q  r)
2.2. (P  q)  r  p  (q  r)
3. Leyes Conmutativas
3.1. P  q  q  p
3.2. P  q  q  p
4. Leyes Distributivas
4.1. P  ( q  r )  ( p  q )  (p  r)
4.2. P  ( q  r )  ( p  q )  (p  r)
5. Leyes de Identidad
5.1. P  F  P
5.2. P  F  F
5.3. P  V  V
5.4. P  V  P
6. Leyes de Complementación
6.1. P   P  V (tercio excluido)
6.2. P   P  F (contradicción)
6.3.   P  P (doble negación)
6.4.  V  F,  F  V

14. LEYES DEL ALGEBRA DE PROPOSICIONES
7. Leyes De Morgan
7.1.  ( P  q )   P   q
7.2.  ( P  q )   P   q
Otras Equivalencias Notables
a. p q   p  q (Ley del condicional)
b. p q  (p q)  (q p) (Ley del bicondicional)
c. p  q  ( p   q )  ( q   p ) (Ley de disyunción exclusiva)
d. p q   q  p (Ley del contrarrecíproco)
e. p  q   (  p   q )
f. ( (p  q )  r )  ( p  r )  (q  r ) (Ley de demostración por casos)
g. (p q)  (p   q F) (Ley de reducción al absurdo)
Nota: Todas las equivalencias que aparecen en ambos cuadros pueden ser
probadas. Para esto, sólo se tiene que verificar que el bicondicional
correspondiente es una tautología

15. Equivalencia e Implicación lógica
Definición: Sean A y B dos formas proposicionales.
Se dice que A Implica Lógicamente a B, o simplemente A implica a B, y se
escribe: AÞ B si el condicional A® B es una tautología
Proposiciones Equivalentes
Sean A y B dos formas proporsicionales. Diremos que A es Lógicamente
Equivalente a B, o simplemente que A es equivalente a B, y escribimos
A º B o A Û B,
Si y sólo si la forma bicondicional A Û B es una tautología.
Razonamientos:
Definición: Un razonamiento o una inferencia es la aseveración de que una
proposición, llamada conclusión es consecuencia de otras proposiciones
dadas llamadas premisas.

16. Forma Proposicional de un Razonamiento
Un razonamiento con premisas P1, P2, P3, P4, & .., Pn y conclusión C lo
escribiremos en forma proposicional como:
P1
P2
P3
P4
.
.
.
Pn
Métodos de Demostración
Demostración Directa
En la demostración directa debemos probar una implicación:
P Þ q. Esto es, llegar a la conclusión q a partir de la premisa p mediante una
secuencia de proposiciones en las que se utilizan axiomas, definiciones,
teoremas o propiedades demostradas previamente.

17. Demostración Indirecta
Dentro de este método veremos dos formas de demostración:
Método del Contrarrecíproco: Otra forma proposicional equivalente a p®
C nos proporciona la Ley del contrarrecíproco: P ® C º ~ C ® ~ P.
Esta equivalencia nos proporciona otro método de demostración, llamado el
método del contrarrecíproco, según el cual, para demostrar que pÞ C, se
prueba que ~ C Þ ~ P.
Demostración por Reducción al Absurdo: Veamos que la proposición p Þ
q es tautológicamente equivalente a la proposición (p Ù ~ q) Þ (r Ù ~ r) siendo
r una proposición cualquiera, para esto usaremos el útil método de las tablas
de verdad.

18. CONCLUSION
 Luego de la lectura del texto entendemos las diferentes formas de
resolver enunciados que contiene una o varia proposiciones ya
que de manera lógica se dan valores a dichas proposiciones que
nos permiten resolverlos. A medida que vamos obteniendo
conocimiento sobre el tema nos damos cuenta como le vamos
dando forma a los enunciados, ya que nos permite desde el punto
de vista matemático llegar a resolver ejercicios con mayor
facilidad analizando mejor los enunciados y aplicando mejor las
herramientas matemáticas. Cabe destacar que también este tema
nos ayuda a obtener mayor y mejor conocimiento al momento de
estudiar los circuitos lógicos ya que nos ayudara a entender como
es que las compuerta que están dentro de dichos circuitos
funcionan . Es importante hacer resaltar que el tema es una
herramienta valiosa para muchos aspecto, y es aplicable en la
mayoría de las materias que se estudian en la carrera de
ingeniería por lo cual es de suma importancia su estudio

19. BIBLIOGRAFIA:
 http://saiaead.uft.edu.ve/ead/mod/assign/view.php
?id=195047
 Saenz J. 2006, Fundamentos de la Matemática,
Inversora Hipotenusa