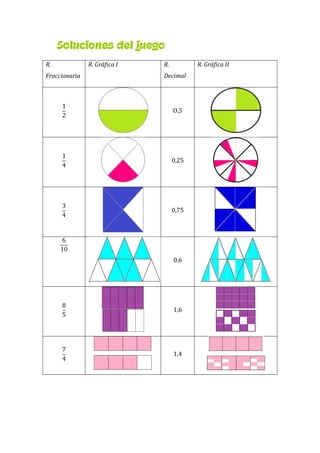
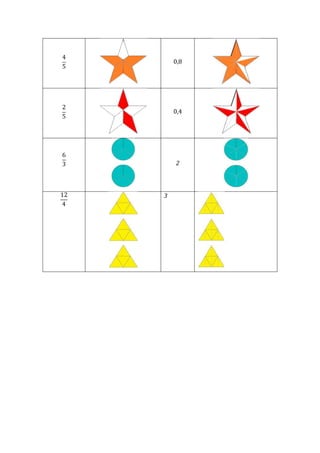
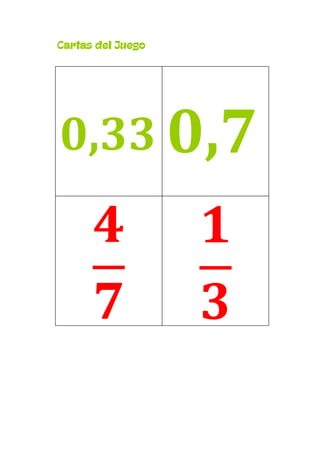
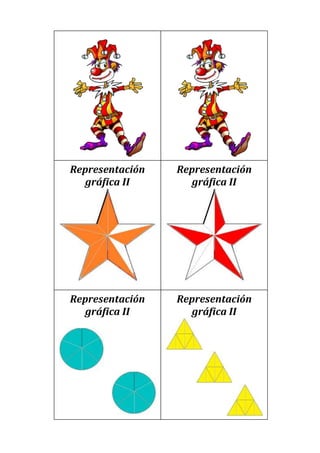
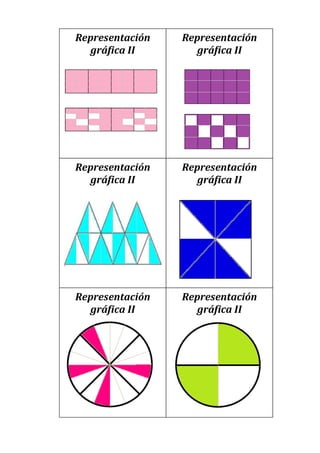
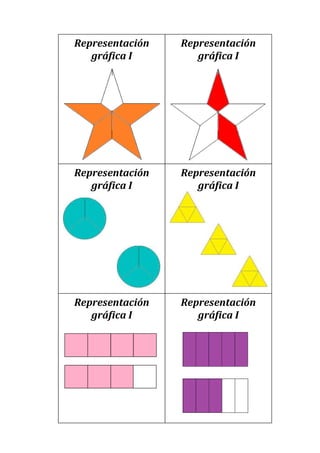
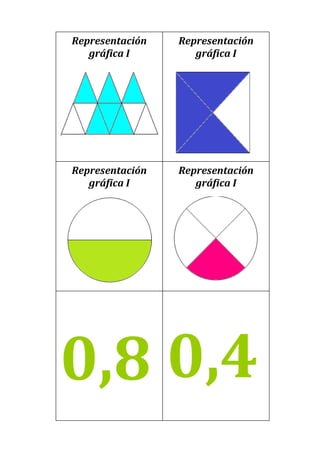
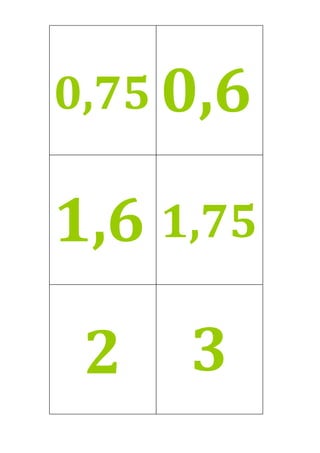
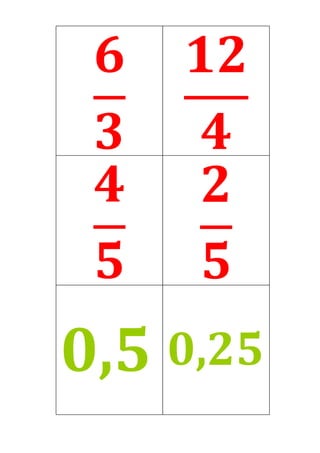
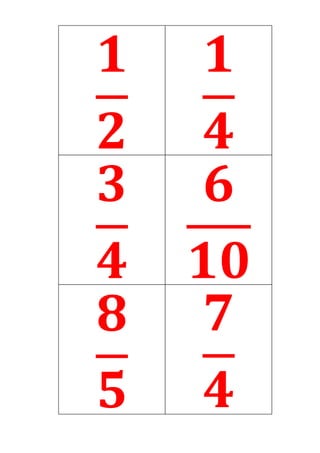
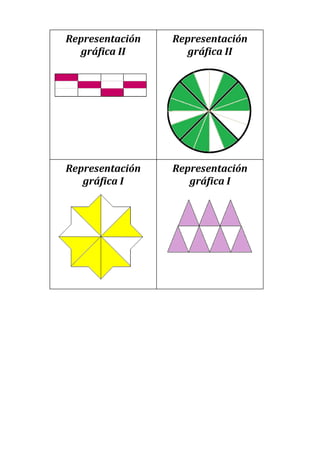
Este documento presenta un plan de clase para enseñar fracciones a estudiantes de 1°4 Liceo N°3. La clase dura 45 minutos y se centra en consolidar las representaciones de fracciones (gráficas, fraccionarias y decimales) a través de un juego grupal llamado "Las Pandillas". Los estudiantes trabajarán en equipos para identificar las diferentes representaciones de números fraccionarios en cartas. Luego se realizará una puesta en común para revisar los resultados.