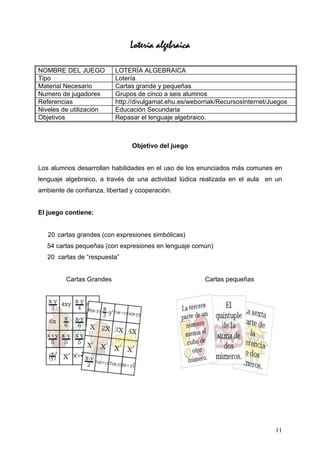
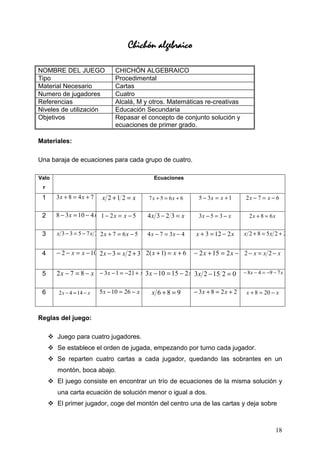
Este documento presenta 20 juegos matemáticos que pueden ser utilizados por profesores de educación secundaria para hacer sus clases más creativas y lúdicas. Los juegos cubren una variedad de temas matemáticos como áreas y perímetros, factorización de polinomios, valor absoluto, números racionales y lenguaje algebraico. El autor explica cómo cada juego puede ser utilizado en el aula para reforzar conceptos matemáticos de manera divertida.