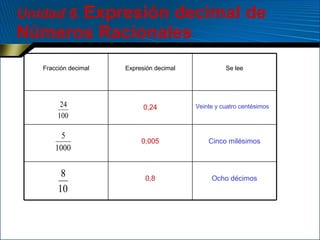
Un número racional es decimal si su denominador es una potencia de 2, 5 o el producto de ambos, lo que permite expresarlo como una fracción decimal finita. Los números racionales no decimales no pueden expresarse como fracciones decimales finitas porque sus restos comienzan a repetirse de forma periódica e infinita al dividir el numerador entre el denominador. Los números decimales pueden ser exactos o periódicos puros o mixtos, y en cada caso su expresión decimal está relacionada con una fracción generatriz.

1. Expresión decimal de Números Racionales Manuel Martínez [email_address]

2. . Expresión decimal de Números Racionales Un número es racional decimal si admite una representación fraccionaria decimal Para que un número racional sea decimal , su denominador tiene que ser potencia de 2 , de 5 o producto de ambas Al dividir numerador para denominador de racionales decimales se obtiene resto 0 y la expresión con coma que resulta es finita .

3. Unidad 6 . Expresión decimal de Números Racionales 3/4 es un racional decimal porque 4= 2x2 7/25 es racional decimal porque 25 = 5 2 6/5 es racional decimal porque 5 = 5x1 3/40 es racional decimal porque 40 = 2 3 x5 : Son fracciones decimales

4. Unidad 6 . Expresión decimal de Números Racionales Un número es racional no decimal si no admite una representación fraccionaria decimal Al dividir numerador por denominador de racionales no decimales , en algún momento los restos comienzan a repetirse y la expresión con coma que resulta es infinita periódica

5. Unidad 6 . Expresión decimal de Números Racionales Son ejemplos de racionales no decimales : 1/3 porque 3 no es potencia de 2, de 5 ni del producto de ambos 19/60,porque 60 = 2 2 x 3 x 5 15/22 porque 22 = 2 x 11

6. Unidad 6 . Expresión decimal de Números Racionales Generatriz de un n úmero decimal De un número decimal exacto decimal exacto fracción generatriz De un número decimal periódico puro Decimal periódico puro De un número decimal periódico mixto fracción generatriz fracción generatriz

7. Unidad 6 . Expresión decimal de Números Racionales Ocho décimos 0,8 Cinco milésimos 0,005 Veinte y cuatro centésimos 0,24 Se lee Expresión decimal Fracción decimal