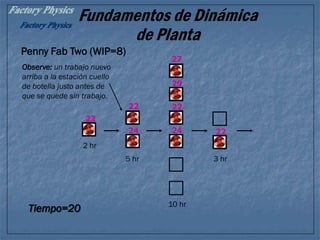
El documento define conceptos clave relacionados con la dinámica de plantas, incluyendo workstation, partes, producto final, consumibles, ruta, orden, trabajo, throughput, capacidad, inventario de materia prima, inventario de producto terminado, trabajo en proceso, rotación de inventario, tiempo de ciclo, lead time, utilización, tasa de cuello de botella y tiempo de proceso bruto. Además, presenta ejemplos numéricos para ilustrar cómo varían estos parámetros con diferentes niveles de trabajo en proceso para una línea de