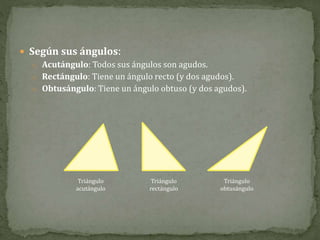
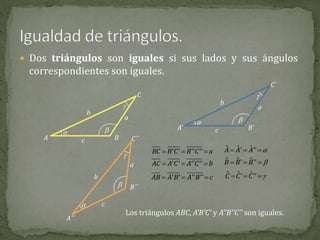
Este documento define y describe conceptos básicos de geometría plana como polígonos, triángulos, cuadriláteros, círculos y simetría. Define líneas poligonales, polígonos, sus elementos y clasificaciones. Explica las propiedades de triángulos, cuadriláteros y polígonos regulares, e introduce conceptos como circunferencias, sectores y otros elementos relacionados con círculos. Por último, define ejes de simetría en figuras geométricas.

3.  Línea poligonal es aquélla formada por varios segmentos
consecutivos.
 Una línea poligonal puede ser abierta o cerrada.
Línea poligonal cerradaLínea poligonal abierta

4.  Polígono es la región del plano limitada por una línea
poligonal cerrada.
Polígono

5.  Lado: Cada uno de los segmentos que encierran el
polígono.
 Vértice: Cada uno de los puntos en los que se unen dos
lados.
 Diagonal: Segmento que une dos vértices no consecutivos.
 Ángulo interior: Ángulo formado por dos lados
consecutivos.
 Ángulo exterior: Ángulo formado por un lado y la
prolongación del consecutivo.

6. Lado
Vértice
Diagonal
Ángulo interior
Ángulo exterior

7. Nº de vértices
Nº de diagonales
desde cada vértice
Nº de diagonales
totales
3 0 0
4 1
5 2
6 3
1 4
2
2


2 5
5
2


3 6
9
2



8. Nº de vértices
Nº de diagonales
desde cada vértice
Nº de diagonales
totales
n n3
 3
2
n n 
En general:

9.  Suma de ángulos interiores de un triángulo:





 +  +  = 180

10.  Suma de ángulos interiores de un polígono de n lados:
Nº de
vértices
Nº de
diagonales
desde cada
vértice
Nº de
triángulos
Suma de ángulos interiores
4 1 2 1802=360
5 2 3 1803=540
6 3 4 1804=720
n n-3 n-2 180(n-2)

11.  Suma de ángulos exteriores:










 +  +  +  +  =360

12.  Según la medida de sus ángulos interiores:
o Cóncavo: Algún ángulo interior mide más de 180.
o Convexo: Todos los ángulos interiores miden menos de
180.
Cóncavo Convexo

13.  Según el número de lados:
o Triángulo: Polígono de tres lados.
o Cuadrilátero: Polígono de cuatro lados.
o Pentágono: Polígono de cinco lados.
o Hexágono: Polígono de seis lados.
o Heptágono: Polígono de siete lados.
o Octógono: Polígono de ocho lados.
o Eneágono: Polígono de nueve lados.
o Decágono: Polígono de diez lados…
Triángulo Cuadrilátero Pentágono Hexágono
Heptágono Octógono Eneágono Decágono

14.  Según su forma:
o Equiláteros: Polígonos de lados iguales.
o Equiángulos: Polígonos de ángulos iguales.
o Regulares: Polígonos de lados y ángulos iguales.
Polígono
equilátero
Polígono
equiángulo
Polígono
regular

16.  Triángulo es un polígono de tres lados.
A
C
B
a
b
c

17.  Base: Es el lado sobre el que se considera que se apoya el
triángulo.
 Altura: Es la recta perpendicular a la base que pasa por el
vértice opuesto a dicha base.
Base
Altura

18.  Según sus lados:
o Equilátero: Todos sus lados son iguales.
o Isósceles: Dos lados iguales y uno desigual.
o Escaleno: Tres lados distintos.
Triángulo
equilátero
Triángulo
isósceles
Triángulo
escaleno

19.  Según sus ángulos:
o Acutángulo: Todos sus ángulos son agudos.
o Rectángulo: Tiene un ángulo recto (y dos agudos).
o Obtusángulo: Tiene un ángulo obtuso (y dos agudos).
Triángulo
acutángulo
Triángulo
rectángulo
Triángulo
obtusángulo

20.  Dos triángulos son iguales si sus lados y sus ángulos
correspondientes son iguales.
A
C
B
a
b
c
 

A’
C´
B’
a
b
c
 

A´´
C´´
B´´
a
b
c


' ' '' ''BC B C B C a  
' ' '' ''AC A C A C b  
' ' '' ''AB A B A B c  
ˆ ˆ ˆ' ''A A A   
ˆ ˆ ˆ' ''B B B   
ˆ ˆ ˆ' ''C C C   
Los triángulos ABC, A’B’C’ y A’’B’’C’’ son iguales.

21.  Criterios de igualdad de triángulos:
1. Dos triángulos con los tres lados correspondientes iguales, son dos
triángulos iguales.
2. Dos triángulos con dos lados correspondientes iguales y el ángulo
comprendido entre ellos también igual, son dos triángulos iguales.
3. Dos triángulos con un lado correspondiente igual y los dos ángulos
contiguos a él también iguales, son dos triángulos iguales.
b a
c
b a
c
a
b 
a
b 
a

a

Criterio 1. Criterio 3.Criterio 2.

22.  Mediatriz de un segmento es la recta perpendicular al
segmento que pasa por su punto medio.
 Circuncentro es el punto en el que se cortan las tres
mediatrices de los lados de un triángulo, pues es el centro
de la circunferencia circunscrita al triángulo.
ma = mediatriz sobre el lado a
mb = mediatriz sobre el lado b
mc = mediatriz sobre el lado c
Co = circuncentro
r = radio de la circunferencia circunscrita
A
Co
C
B
mamb
mc
r
a
b
c
c/2 c/2

23.  Bisectriz de un ángulo es la recta que divide el ángulo en
dos partes iguales.
 Incentro es el punto en el que se cortan las tres bisectrices
de los ángulos de un triángulo, pues es el centro de la
circunferencia inscrita al triángulo.
bA = bisectriz del ángulo A
bB = bisectriz del ángulo B
bC = bisectriz del ángulo C
Io = incentro
r = radio de la circunferencia inscrita
A
C
B
ab
c
bA
bB
bC
Io
r
Â/2
Â/2

24.  Mediana es la línea recta que une un vértice con el punto
medio del lado opuesto.
 Baricentro es el punto en el que se cortan las tres
medianas de un triángulo.
mea = mediana sobre el lado a
meb = mediana sobre el lado b
mec = mediana sobre el lado c
G = baricentro
A
C
B
ab
c/2
mea
meb
mec
G
c
c/2
Nota: La distancia del baricentro a un vértice es doble que la
distancia del baricentro al punto medio del lado opuesto.

25.  Altura es la línea recta perpendicular a un lado (o a su
prolongación) trazada desde el vértice opuesto.
 Ortocentro es el punto en el que se cortan las tres alturas
de un triángulo.
ha = altura sobre el lado a
hb = altura sobre el lado b
hc = altura sobre el lado c
Oo = ortocentro
A
C
B
ab
c
Ooha
hb
hc

27.  Un cuadrilátero es un polígono de cuatro lados.
A
B
C
D

28.  Paralelogramos: Cuadriláteros cuyos lados son paralelos dos a dos.
Rectángulo Cuadrado Romboide Rombo
Trapecio Trapecio isósceles Trapecio rectángulo
Trapezoide
 Trapecios: Cuadriláteros con dos lados paralelos y los otros dos no
paralelos.
 Trapezoides: Cuadriláteros sin lados paralelos.

30.  Polígono regular es aquel cuyos lados y ángulos miden lo
mismo.
l l

l
l
l
l
l


 


31.  Centro: Punto del que equidistan todos los vértices del polígono.
 Radio: Segmento que une el centro con un vértice.
 Apotema: Segmento que une el centro con el punto medio de un lado.
 Ángulo central: Ángulo determinado por dos radios.
2
l
2
l
RadioApotema
l
Ángulo central

33.  Círculo es la región del plano encerrada por una
circunferencia.
r

34.  Sector circular es la porción de círculo comprendida entre
dos radios.
r


35.  Segmento circular es la porción de círculo comprendida
entre un arco de circunferencia y su cuerda
correspondiente.
l

r

36.  Corona circular es la porción de plano comprendida entre
dos circunferencias concéntricas.
r
R

37.  Trapecio circular es la porción de corona circular
comprendida entre dos radios
r
R

39.  Un eje de simetría es una recta que divide en dos partes
iguales una figura.
Eje de simetría

40.  Cuando una figura tiene n ejes de simetría, dos ejes
contiguos forman un ángulo de 180/n.
e1
e2
e3 e4
e5
180
36
5

 