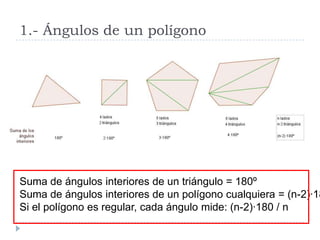
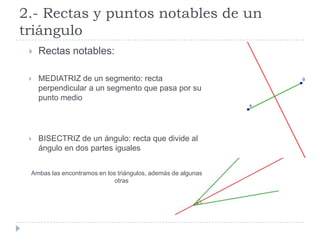
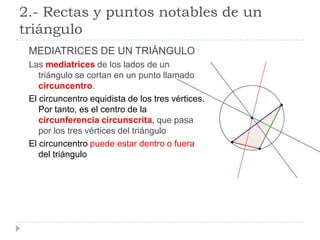
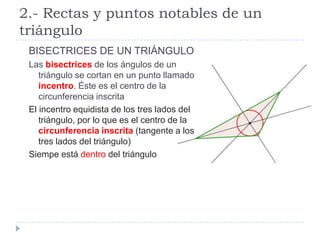
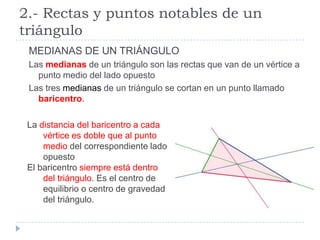
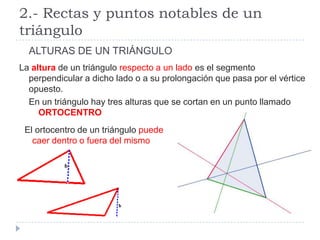
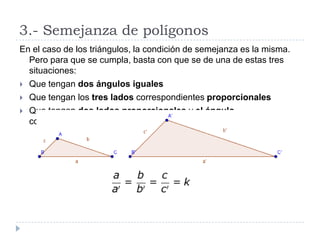
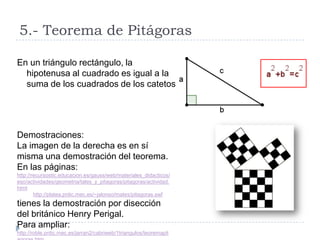
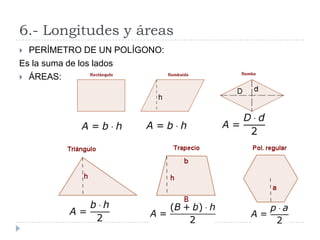
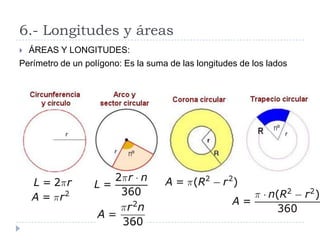
Este documento presenta conceptos básicos de geometría en el plano, incluyendo ángulos de polígonos, rectas y puntos notables de triángulos, semejanza de polígonos, el teorema de Thales, el teorema de Pitágoras, y longitudes y áreas de polígonos. Explica definiciones clave como la suma de ángulos interiores, bisectrices, medianas, y más.

1. LAVADERO DE THALES
de Carlos Esteban Esteban, alumno de 1º Bachillerato
GEOMETRÍA EN EL PLANO
3º ESO, Curso 2011-2012
IES Valle del Jilcoa – Calamocha (Teruel)

2. 1.- Ángulos de un polígono
Suma de ángulos interiores de un triángulo = 180º
Suma de ángulos interiores de un polígono cualquiera = (n-2)·18
Si el polígono es regular, cada ángulo mide: (n-2)·180 / n

3. 2.- Rectas y puntos notables de un
triángulo
 Rectas notables:
 MEDIATRIZ de un segmento: recta
perpendicular a un segmento que pasa por su
punto medio
 BISECTRIZ de un ángulo: recta que divide al
ángulo en dos partes iguales
Ambas las encontramos en los triángulos, además de algunas
otras

4. 2.- Rectas y puntos notables de un
triángulo
MEDIATRICES DE UN TRIÁNGULO
Las mediatrices de los lados de un
triángulo se cortan en un punto llamado
circuncentro.
El circuncentro equidista de los tres vértices.
Por tanto, es el centro de la
circunferencia circunscrita, que pasa
por los tres vértices del triángulo
El circuncentro puede estar dentro o fuera
del triángulo

5. 2.- Rectas y puntos notables de un
triángulo
BISECTRICES DE UN TRIÁNGULO
Las bisectrices de los ángulos de un
triángulo se cortan en un punto llamado
incentro. Éste es el centro de la
circunferencia inscrita
El incentro equidista de los tres lados del
triángulo, por lo que es el centro de la
circunferencia inscrita (tangente a los
tres lados del triángulo)
Siempe está dentro del triángulo

6. 2.- Rectas y puntos notables de un
triángulo
MEDIANAS DE UN TRIÁNGULO
Las medianas de un triángulo son las rectas que van de un vértice a
punto medio del lado opuesto
Las tres medianas de un triángulo se cortan en un punto llamado
baricentro.
La distancia del baricentro a cada
vértice es doble que al punto
medio del correspondiente lado
opuesto
El baricentro siempre está dentro
del triángulo. Es el centro de
equilibrio o centro de gravedad
del triángulo.

7. 2.- Rectas y puntos notables de un
triángulo
ALTURAS DE UN TRIÁNGULO
La altura de un triángulo respecto a un lado es el segmento
perpendicular a dicho lado o a su prolongación que pasa por el vértice
opuesto.
En un triángulo hay tres alturas que se cortan en un punto llamado
ORTOCENTRO
El ortocentro de un triángulo puede
caer dentro o fuera del mismo

8. 2.- Rectas y puntos notables de un
triángulo
TABLA RESUMEN
RECTAS PUNTO SITUACIÓN DIBUJO
Mediatrices Circuncentro Dentro o fuera
Bisectrices Incentro Dentro
Medianas Baricentro Dentro
Alturas Ortocentro Dentro o fuera

9. 3.- Semejanza de polígonos
Dos polígonos son semejantes si tienen sus ángulos correspondientes
iguales y sus lados correspondientes proporcionales
Al resultado de estas divisiones se le llama razón de semejanza
Ejemplo: Un polígono y el mismo fotocopiado y ampliado o reducido, son
semejantes.

10. 3.- Semejanza de polígonos
En el caso de los triángulos, la condición de semejanza es la misma.
Pero para que se cumpla, basta con que se de una de estas tres
situaciones:
 Que tengan dos ángulos iguales
 Que tengan los tres lados correspondientes proporcionales
 Que tengan dos lados proporcionales y el ángulo
comprendido, igual

11. 4.- Teorema de Thales
Veamos dos enunciados. ¿Dicen lo mismo?
 Si dos rectas cualesquiera se cortan por varias
rectas paralelas, los segmentos determinados
en una de las rectas son proporcionales a los
segmentos correspondientes en la otra.
Veamos dos enunciados. ¿Dicen lo mismo?
 Toda recta paralela a un lado de un triángulo que corta a los otros dos
lados, determina un triángulo más pequeño, que es semejante al
primero. De estos triángulos se dice que están en posición de
Thales.

12. 5.- Teorema de Pitágoras
En un triángulo rectángulo, la
hipotenusa al cuadrado es igual a la
suma de los cuadrados de los catetos
Demostraciones:
La imagen de la derecha es en sí
misma una demostración del teorema.
En las páginas:
http://recursostic.educacion.es/gauss/web/materiales_didacticos/
eso/actividades/geometria/tales_y_pitagoras/pitagoras/actividad.
html
http://platea.pntic.mec.es/~jalonso/mates/pitagoras.swf
tienes la demostración por disección
del británico Henry Perigal.
Para ampliar:
http://roble.pntic.mec.es/jarran2/cabriweb/1triangulos/teoremapit

13. 6.- Longitudes y áreas
 PERÍMETRO DE UN POLÍGONO:
Es la suma de los lados
 ÁREAS:

14. 6.- Longitudes y áreas
 ÁREAS Y LONGITUDES:
Perímetro de un polígono: Es la suma de las longitudes de los lados