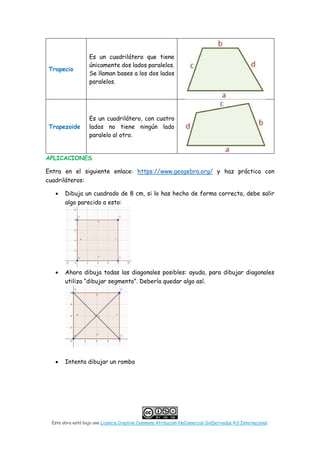
Este documento presenta el temario y objetivos de la unidad 2 sobre figuras planas elementales. Cubre definiciones, características y tipos de triángulos, cuadriláteros, polígonos y círculos. Incluye ejemplos y ejercicios prácticos para construir estas figuras geométricas usando GeoGebra.

1. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
BLOQUE III Geometría.
UNIDAD 2 Figuras planas elementales: triángulo, cuadrado, figuras
poligonales.
Objetivos del bloque:
1. Elementos básicos de la geometría del plano.
2. Relaciones y propiedades de figuras en el plano: Paralelismo y
perpendicularidad.
3. Ángulos y sus relaciones.
4. Construcciones geométricas sencillas: mediatriz, bisectriz.
5. Propiedades.
6. Figuras planas elementales: triángulo, cuadrado, figuras poligonales.
7. Clasificación de triángulos y cuadriláteros.
8. Propiedades y relaciones.
9. Medida y cálculo de ángulos de figuras planas.
10. Cálculo de áreas y perímetros de figuras planas.
11. Cálculo de áreas por descomposición en figuras simples.
12. Circunferencia, círculo, arcos y sectores circulares.
13. Resolución de problemas geométricos sencillos.
14. Interés por las diferentes producciones culturales y artísticas en donde
aparezcan los elementos estudiados (películas, cortos, videos artísticos,
animación, documentales, publicidad).
15. Interés y disfrute de las posibilidades que nos ofrecen los diferentes
entornos artísticos: museos, exposiciones, galerías de arte, auditorios,
teatros, páginas web y blogs de museos, exposiciones artísticas, galerías de
arte.
16. Respeto y valoración de las distintas manifestaciones artísticas.
17. Expresión crítica de sus conocimientos, ideas, opiniones y preferencias
respecto a las manifestaciones artísticas.
Procedimiento:
1. Los apuntes como los ejercicios se deben realizar en el cuaderno de clase.
Ten en cuenta, que, dentro de la evaluación de esta unidad, hay una prueba
que se hace con los apuntes.
2. Utilizamos bolígrafo de color negro para los apuntes, de color verde, para los
títulos, azul, para los enunciados de los problemas y el lápiz para la resolución
de estos.

2. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
Evaluación:
Actitud en
clase
Cuaderno
Examen con
apuntes
Examen sin
apuntes
Nota Final
10% 20% 30% 40% 100%
Temario:
1. El triángulo.
2. El cuadrilátero.
3. Los polígonos.
4. El circulo y la circunferencia
1. El triángulo.
Definición
Es un polígono de tres lados, es una figura rígida.
A, B y C corresponde a los ángulos del triángulo y a sus vértices.
a, b y c corresponde a los lados del triángulo.
Características
• Todo triángulo consta de 3 vértices que son las intersecciones de las rectas.
• Los segmentos que unen los vértices se llaman lados del triángulo, y hay tres.
• Los lados del triángulo forman tres ángulos que se llaman ángulos internos del
triángulo.
• En todo triángulo los ángulos internos suman 180º
Base de un triángulo: es el lado sobre el que se apoya.
Altura de un triángulo: La altura de un triángulo es el segmento perpendicular que va

3. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
desde un vértice al lado opuesto o a la prolongación de éste.
1. Fuente: https://matematicasiesoja.files.wordpress.com/2013/10/angulos-y-triangulos.pdf
Tipos de triángulos
a) En relación con los lados:
Equilátero
Tres lados iguales, y los ángulos
iguales
Isósceles
Dos lados iguales y un tercero
desigual
Escaleno Los tres lados desiguales
b) En relación con los ángulos:
Acutángulo
Todos sus ángulos son agudos, es
decir menores de 90º
Obtusángulo
El que tiene algún ángulo obtuso, es
decir mayor a 90º
Rectángulo
El que tiene un ángulo recto, es decir,
un ángulo que mide 90º. Los dos
lados que forman el ángulo recto se
llaman catetos y la otra hipotenusa.

4. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
Visualiza el siguiente video: https://youtu.be/3gWdbpe49ng
APLICACIONES
Entra en el siguiente enlace: https://www.geogebra.org/
• Pincha sobre el enlace: GeoGebra Clásico
• Pincha sobre el siguiente icono: y luego selecciona polígono
Vamos a construir un triangulo rectángulo. Situamos el puntero en las coordenadas
(0,0); luego sobre el eje de la X, situamos otro punto a 5 cm de distancia, y sobre el
eje de la Y, situamos otro punto a 3 cm, y luego volvemos con el puntero al punto
inicial o A. Si lo habéis hecho de forma correcta, la imagen que debería salir es la
siguiente:
Haz varias pruebas cambiando las medidas de los lados, probando otros tipos de
triángulos.
2. El cuadrilátero
Definición
Es un polígono de cuatro lados y cuatro vértices
Características
• Tienen cuatro lados.
• Tienen cuatro vértices.
• Tienen dos diagonales: segmentos cuyos extremos son dos vértices no
contiguos. Divide al cuadrilátero en triángulos.

5. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
• Tienen cuatro ángulos interiores.
Tipos
Cuadrado
Es un cuadrilátero regular, es
decir, una figura plana de
cuatro lados iguales y cuatro
ángulos interiores rectos, es
decir 90º. La suma de todos sus
ángulos es 360º
Rombo
Es un cuadrilatero, cuyos
cuatro lados son de igual
longitud y sus diagonales
forman cuatro ángulos rectos.
Los pares de lados opuestos
son iguales y paralelos dos a
dos. Hay una diagonal mayor y
otra menor.
Rectángulo
Es un cuadrilátero, cuyos
ángulos son rectos, donde los
lados opuestos tienen la misma
longitud.
Romboide
Es un cuadrilátero que tiene
lados contiguos desiguales y no
tiene ángulos rectos.

6. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
Trapecio
Es un cuadrilátero que tiene
únicamente dos lados paralelos.
Se llaman bases a los dos lados
paralelos.
Trapezoide
Es un cuadrilátero, con cuatro
lados no tiene ningún lado
paralelo al otro.
APLICACIONES
Entra en el siguiente enlace: https://www.geogebra.org/ y haz práctica con
cuadriláteros:
• Dibuja un cuadrado de 8 cm, si lo has hecho de forma correcta, debe salir
algo parecido a esto:
• Ahora dibuja todas las diagonales posibles: ayuda, para dibujar diagonales
utiliza “dibujar segmento”. Debería quedar algo así.
• Intenta dibujar un rombo

7. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
3. Los polígonos.
Definiciones
La línea poligonal: es un conjunto de segmentos concatenados, (cada uno empieza
donde acaba el anterior); se clasifican en abiertos o cerrados.
Abierto Cerrado
Polígono: es la superficie contenida por una línea poligonal cerrada.
Tipos
Según sus ángulos: pueden ser de dos tipos, convexos o cóncavos.
• Convexos, todos sus ángulos interiores son inferiores a 180º
• Cóncavo, algunos de sus ángulos interiores son superior a 180º

8. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
Convexo Cóncavo
Según sus lados: se pueden clasificar en regulares o irregulares.
• regular, cuando todos sus lados miden igual.
• irregular, cuando sus lados no miden igual.
Ejemplos de polígonos que estudiaremos en este curso
Este curso estudiaremos los polígonos regulares, para ello debemos saber los
elementos:
• lado, cada uno de los segmentos de la línea poligonal cerrada.
• vértice, cada uno de los puntos comunes a dos lados consecutivos.
• centro, punto que equidista de todos los vértices
• apotema y radio; apotema: segmento que une el centro del polígono con el
punto medio de cada lado; y radio: segmento que une el centro del polígono
con cada uno de los vértices.
• diagonal, segmento cuyos extremos son dos vértices no consecutivos.
• ángulo interior, cada uno de los ángulos formados por dos vértices no
consecutivos.

9. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
Cada polígono regular recibe un nombre según su número de lados:
• tres lados, ejemplo un triángulo equilátero.
• cuatro lados, ejemplo el cuadrado.
• cinco lados, pentágono
• seis lados, hexágono
• siete lados, heptágono
• ocho lados, octágono
• nueve lados, eneágono
• diez lados, decágono
• once lados, endecágono
• doce lados, dodecágono
Visualiza los siguientes videos, de cómo construir polígonos:
• https://youtu.be/S6XYNLLajmE
• https://youtu.be/WuwIBpnrKxI
• https://youtu.be/kLK1BUPgcAU
• https://www.arturogeometria.com/los-poligonos
4. El circulo y la circunferencia.
Definiciones
Un círculo es el lugar geométrico de los puntos cuya distancia a un punto fijo (el
centro C) es menor o igual que una constante r, llamada radio.

10. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
La circunferencia es una figura geométrica cerrada cuyos puntos están a una
distancia constante r, llamada radio, del centro (C).
La circunferencia es el perímetro del círculo.
Elementos de un circulo
• Centro: el centro C es un punto fijo interior, equidistante de su perímetro (o
circunferencia) a una distancia igual al radio.
• Radio: es el segmento r que une el centro (C) del círculo con cualquier punto
del perímetro de éste.
• Diámetro: segmento D que une dos puntos del perímetro del círculo pasando
por el centro (C). Su longitud es el doble que la del radio.
• Cuerda: es un segmento K que une dos puntos del perímetro del círculo sin
pasar por el centro.

11. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
• Arco: es la parte del perímetro del círculo (a) que queda entre los dos
extremos de una cuerda.
• Punto interior: punto que pertenece al círculo (I), encontrándose a una
distancia del centro menor o igual que r.
• Punto exterior: puntos que están fuera del círculo (E), es decir, a una
distancia del centro mayor que r.
• Ángulo central: es el ángulo comprendido entre dos segmentos (o radios) que
van del centro a dos puntos del perímetro del círculo (α). Un ángulo central
determina un arco.
• Tangente: es una recta (a) con un único punto común con el perímetro del
círculo. El radio es perpendicular a la tangente en el punto de tangencia.
• Secante: es una recta (a) que corta el perímetro del círculo en dos puntos.
• Ángulo inscrito: ángulo (β) que forman dos cuerdas que coinciden en un mismo
punto de la circunferencia. Es decir, es el ángulo que generan tres puntos de
ésta.

12. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
APLICACIONES
Entra en el siguiente enlace: https://www.geogebra.org/ y haz práctica con circulos:
sigues las indicaciones.
EJERCICIOS.
1. Construye un triangulo equilátero de base 5 cm. Indica sus lados, sus vértices y
mide sus ángulos.
2. Construye un triángulo isósceles de base 3,5 cm y altura 8 cm. Indica sus lados,
sus vértices y mide sus ángulos.
3. Construye un triángulo escaleno cuya base es 12 cm. Indica sus lados, sus vértices
y mide sus ángulos.
4. Construye un ejemplo de triángulo acutángulo. Indica sus lados y lo que miden, sus
vértices y mide sus ángulos.
5. Construye un ejemplo de triángulo obtusángulo, con base 5 cm. Indica sus lados y
lo que miden, sus vértices y mide sus ángulos.
6. Construye un ejemplo de triángulo rectángulo, con base 8 cm y altura 5 cm. Indica
sus lados y lo que miden, sus vértices y mide sus ángulos.
7. Todos estos triángulos son escalenos, explica por qué. Y clasifícalos según la
relación de sus ángulos:
a) b) c)

13. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
8. Construye los siguientes cuadriláteros según te indican:
a) Un cuadrado de 4 cm
b) Un rectángulo de base 12 cm y altura 5 cm
c) Un rombo, cuyo lado mide 3 cm
d) Un romboide, los lados más largos deben medir 10 cm, y los más cortos 4 cm
e) Un trapecio, cuya base mayor es de 8 cm
f) Un ejemplo de trapezoide
9. Dibuja todas las diagonales posibles de las figuras del ejercicio anterior.
10. Dibuja una línea poligonal con siete lados.
11. Dibuja un ejemplo de polígono abierto y otro de polígono cerrado.
12. De los siguientes polígonos, indica cuales son convexos y cuales cóncavos:
13. Dibuja un pentágono, y señala todos sus elementos.
14. De la figura anterior, dibujar todo su ángulo, todos los radios, todas las apotemas,
y todas las diagonales.
15. Construye un pentágono conociendo su lado base, que mide 6 cm.
16. En el siguiente circulo, indica que elementos se han señalado:

14. Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
17. Con la ayuda del compás, dibujar un circulo de 5 cm de radio. Señala todos los
elementos de un circulo.