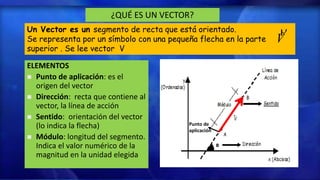
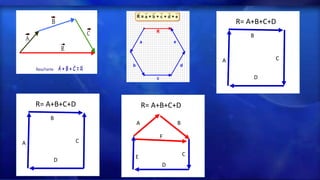
Este documento presenta conceptos sobre análisis vectorial, incluyendo definiciones de vectores, tipos de vectores, operaciones con vectores colineales y concurrentes, y métodos para hallar la resultante de vectores. Explica cómo sumar vectores colineales y concurrentes usando métodos gráficos como el paralelogramo, triángulo y polígono, y el método analítico de la ley de los cosenos.

1. PROFESORA RELLA VARGAS SANCHEZ
CIENCIA TECNOLOGIA Y AMBIENTE

2. SABERES PREVIOS
¿QUÉ IMÁGENES REPRESENTAN MAGNITUDES ESCALARES Y CUALES
MAGNITUDESVECTORIALES?
2 100 Km
P
C

3. ANALISIS VECTORIAL
• VECTOR
• ELEMENTOS DE UN VECTOR
• TIPOS DE VECTORES
• OPERACIONES CON VECTORES
• ADICION DE VECTORES COLINIALES
• RESULTANTE MAXIMA
• RESULTANTE MINIMA
• ADICION DE VECTORES CONCURRENTES
• METODOS GRAFICOS
• METODO DEL PARALELOGRAMO
• METODO DEL TRIANGULO
• METODO DEL POLIGONO
• METODO ANALITICO
• LEY DE LOS COSENOS

4. ELEMENTOS
 Punto de aplicación: es el
origen del vector
 Dirección: recta que contiene al
vector, la línea de acción
 Sentido: orientación del vector
(lo indica la flecha)
 Módulo: longitud del segmento.
Indica el valor numérico de la
magnitud en la unidad elegida
¿QUÉ ES UN VECTOR?
Un Vector es un segmento de recta que está orientado.
Se representa por un símbolo con una pequeña flecha en la parte
superior . Se lee vector V
Punto de
aplicación
V


5. COLINEALES.- Si se encuentran sobre la misma línea de acción.
CONCURRENTES.- Si sus líneas de acción concurren en un mismo punto.
A
C
B
Punto de
Concurrencia
A B C
¿TIPOS DE VECTORES?

6. PARALELOS.- Cuando las
líneas de acción son
paralelas.
A
B
C
COPLANARES: Cuando los
vectores se encuentran en un
solo plano.

7. A -A
VECTORES OPUESTOS: Son
iguales en tamaño (Módulo)
pero sentidos opuestos. Los
vectores opuestos son
paralelos:
son vectores
opuestos, por lo tanto, son
paralelos
AA


VECTORES IGUALES:
Si tienen su módulo,
dirección y sentido
iguales
α β
A B
 
 BA


8. ¿QUÉ TIPOS DE VECTORES SE APLICAN EN LAS IMÁGENES?
Evaluamos lo que aprendimos
1 2
3
4
5

9. ADIESTRAND
O NUESTRA
CAPACIDAD
DE VISION

12. CONSTRUYENDO VECTORES
Aplicamos lo que aprendimos
USANDO LA ESCUADRA Y EL TRANSPORTADOR CONSTRUYE LOS SIGUENTES VECTORES.
En cada dibujo indica la escala que utilizaste
A= 3cm < 0°

13. C= 12N < 60°
Escala 1cm=3N
4cm=12N
60°
C


14. 30°
B

B= 5N < 30°
Escala 1N=1cm
5N=5cm

15. USANDO LA ESCUADRA Y EL TRANSPORTADOR CONSTRUYE LOS
SIGUENTES VECTORES.
En cada dibujo indica la escala que utilizaste
P= 40N < 45° M= 60km/h < 120° B= 30m/s2 < 60°

16. Consiste en reemplazar a un conjunto de vectores por un único vector
llamado FUERZA RESULTANTE
ADICION DE VECTORES COLINEALESY/O PARALELOS
A B R=A-B
A B R=A+B
+ =
+ =
Cuando tienen la misma dirección y sentido contrario, el sentido del vector suma o
Resultante estará dado por el vector que tiene mayor magnitud o módulo.
La adición de vectores colineales se realiza por la suma directa de sus módulos
teniendo en cuenta sus signos. El vector resultante tendrá la misma dirección y
sentido que los vectores sumandos.
(Resultante máxima Rmáx= A+B )
(Resultante mínima Rmin= A-B )
OPERACIÓN CON VECTORES

17. Piensa, por ejemplo, en dos caballos que tiran de un carro. En este caso, cuando dos o
más fuerzas actúan a la vez, sus efectos se suman.
Mismo sentido: se suman los módulos de los vectores a componer.
N4F1 

N3F2 

1F

2F

F1

2F

R 

Analíticamente: R = 4N + 3N= 7N

18. Ejemplo, dos niños disputándose un paquete de dulces.
N5F1 

N3F2 

1F

2F

Analíticamente:
R = F1 - F2= 5N-3N= 2N
F1

2F

R 


19. A
B
uA 2|| 
uB 3|| 
 
C uC 5|| 
|R|
B
A
R
Hallar el vector resultante en los siguientes casos:
A
C
B
A=8u B=6u C=4u
B
A
C
1. La resultante máxima de dos vectores es 9 y
la mínima es 1. ¿Cuál es el módulo de cada
vector?
2
1
3 4

20. Este método se usa cuando dos
vectores forman un ángulo
diferente de cero entre sí.
Se construye el paralelogramo
trasladando los vectores a un
punto de aplicación común
conservando su dirección y
sentido, luego se trazan paralelas
por los extremos de cada vector.
La RESULTANTE de los dos
vectores queda determinada en
valor, dirección y sentido por la
diagonal que une el origen con el
vértice opuesto.
MÉTODO DEL PARALELOGRAMO
AI
BI
A
B
A
B
ADICION DE VECTORES CONCURRENTES
METODOS GRAFICOS
CosABBAR 222


21. Método del triángulo: Para 2
vectores concurrentes coplanares. Se
unen los dos vectores uno a
continuación del otro conservando su
magnitud y sentido,
El vector resultante es el resultado de
unir el origen del primer vector con el
extremo último del segundo vector,
formando así un triángulo.
A
B
A
B
MÉTODO DEL TRIÁNGULO
METODOS GRAFICOS

22. B
A
C
B
A
R
C
Los vectores se trazan uno a
continuación de otro con sus
direcciones, sentidos y
magnitudes; luego se une el
origen del primero con el
extremo del último, éste es el
Vector Resultante.
MÉTODO DEL POLÍGONO
METODOS GRAFICOS

23. Ejemplo : Hallar el vector resultante de la suma de los
siguientes vectores
A B
C
A B
CR = 2
A B
C
R = A + B + C
R= C + C = 2C

24. R= A+B+C+D
A C
D
B
R= A+B+C+D
A C
D
B
R= A+B+C+D
A
D
E
B
C
F

25. Halle la Resultante
A
C
B
a
c
b
d e
  
A = 9
B = 5 C = 6
D = 3

26. Si los vectores forman un ángulo agudo

A
B
R
CosABBAR 222

MÉTODO ANALÍTICO : VECTORES CONCURRENTES
22
BAR 
Si los vectores son perpendiculares

27. Diferencia de vectores concurrentes
A
B
A
B
A
θ
- B
D
D

28. NR
R
CosR
CosABBAR
749
15259
2
1
30259
60)5)(3(253
2
22
22









 
La F1 =3N y F2 = 5N, están aplicadas en el mismo punto O, formando un
ángulo de 60°. Halle el modulo de la fuerza resultante
CosABBAR 222


29. Un barco recorre 100 km hacia el Norte durante el primer día de viaje, 60 km al Noreste el segundo día y
120 km hacia el Este el tercer día. Encuentre el desplazamiento resultante con el método del polígono.
Planteamiento: tome como punto de inicio el origen del viaje y tome una escala apropiada para llevarla a
una hoja de trabajo. Use un transportador y una regla para trazar cada vector de manera que sea
proporcional a su magnitud. La resultante será un vector trazado desde el origen del primer vector hasta
la terminación del último vector.
FIG. 1
Al realizar la medición con una regla, a partir del diagrama a escala se observa que el vector resultante
tiene 10.8 cm de longitud. Por tanto, la magnitud es
•10.8 cm = 10.8 cm x 20 km/1 cm = 216 km
Si se mide el angulo q con un transportador, resulta que la dirección es de 41º, por lo tanto el
desplazamiento resultante es R: 216 km / 41º Notación polar
Procedimiento: Escojamos una escala conveniente,
puede ser 20 km = 1 cm, como se observa en la
figura 1. Utilizando esta escala, notamos que:
•100 km = 100 km x 1cm/ 20 km = 5 cm
•60 km = 60 km x 1 cm/20 km = 3 cm
•120 km = 120 km x 1 cm/20 km = 6 cm

30. rβ
α
R
B
A
Ley de Senos
o
Ley de Lamy

33. RESULTANTE
MAXIMA
R= A + B
RESULTANTE
MINIMA
R= A - B
VECTORES
CONCURRENTES
LEY DE LOS
COSENOS
VECTORES
COLINEALES
CosABBAR 222
