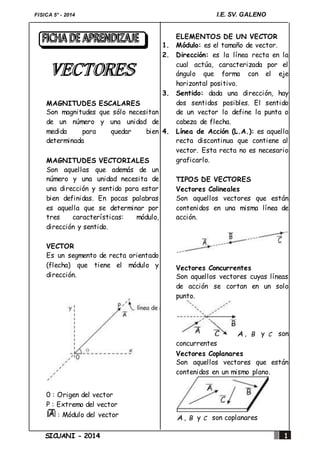
El documento describe conceptos básicos de vectores, incluyendo magnitudes escalares y vectoriales, elementos de un vector, tipos de vectores, suma vectorial y componentes rectangulares de un vector. Explica métodos para sumar vectores como el paralelogramo, polígono y descomposición rectangular, y presenta ejercicios de aplicación de estos conceptos.

1. FISICA 5° - 2014 I.E. SV. GALENOs
SICUANI - 2014 1
MAGNITUDES ESCALARES
Son magnitudes que sólo necesitan
de un número y una unidad de
medida para quedar bien
determinada
MAGNITUDES VECTORIALES
Son aquellas que además de un
número y una unidad necesita de
una dirección y sentido para estar
bien definidas. En pocas palabras
es aquella que se determinar por
tres características: módulo,
dirección y sentido.
VECTOR
Es un segmento de recta orientado
(flecha) que tiene el módulo y
dirección.
0 : Origen del vector
P : Extremo del vector
: Módulo del vector
ELEMENTOS DE UN VECTOR
1. Módulo: es el tamaño de vector.
2. Dirección: es la línea recta en la
cual actúa, caracterizada por el
ángulo que forma con el eje
horizontal positivo.
3. Sentido: dada una dirección, hay
dos sentidos posibles. El sentido
de un vector lo define la punta o
cabeza de flecha.
4. Línea de Acción (L.A.): es aquella
recta discontinua que contiene al
vector. Esta recta no es necesario
graficarlo.
TIPOS DE VECTORES
Vectores Colineales
Son aquellos vectores que están
contenidos en una misma línea de
acción.
Vectores Concurrentes
Son aquellos vectores cuyas líneas
de acción se cortan en un solo
punto.
A , B y C son
concurrentes
Vectores Coplanares
Son aquellos vectores que están
contenidos en un mismo plano.
A , B y C son coplanares

2. Ficha de Aprendizaje FISICA -2014
2
Vectores Paralelos
Son aquellos vectores que tienen
sus líneas de acción paralelas.
Vectores Opuestos
Se llama vector opuesto (–A) de un
vector A cuando tienen el mismo
módulo la misma dirección pero
sentido contrario
* AA 
* ∢ A = ∢–A
* A; –A
SUMA VECTORIAL
Sumar dos o más vectores, es
representarlos por uno sólo
llamado RESULTANTE. Este
vector resultante produce el
mismo efecto que todos juntos.
Hay que tener en cuenta que la
suma vectorial no es lo mismo que
la suma aritmética.
. EDCBAR  .
Método del Paralelogramo
Sirve para sumar dos vectores con
origen común. Se construye el
paralelogramo trazando paralelas a
los vectores dados.
La resultante es la diagonal
trazada desde el origen de los
vectores.
Vectorialmente. = + .
Para calcularsu valor
cos..2222
BABAR  .
O también:
. αcos.B.A.2BAnR 22
 .
Donde:
n  divisor común
Vector Diferencia
Se obtiene uniendo los extremos
de los vectores.
. = – .
. cos..2222
BABAD  .
Caso Particular
Si los vectores forman un ángulo
de 90º, la resultante se obtiene
usando el “Teorema de Pitágoras”

3. FISICA 5° - 2014 I.E. SV. GALENOs
SICUANI - 2014 3
. R2
= A2
+ B2
.
Método del Polígono
Este método consiste en colocar un
vector a continuación del otro,
conservando cada uno de ellos sus
respectivos elementos, donde el
vector resultante se obtiene
uniendo el origen del primer vector
con el extremo del último vector.
. = + + .
NOTA:
SI AL COLOCAR LOS VECTORES UNO A
CONTINUACIÓN DEL OTRO SE
OBTIENE UN POLÍGONO CERRADO, LA
RESULTANTE ES CERO.
Componentes Rectangulares de un
Vector
Son aquellos vectores componentes
de un vector que forman entre sí
un ángulo de 90º.
Descomposición Rectangular
Al sumar varios vectores por el
método de la descomposición
rectangular, se sigue los siguientes
pasos:
1. Descomponer rectangularmente
cada uno de los vectores, según un
par de ejes perpendiculares
previamente elegidos X e Y.
2. Determinar la resultante de cada
eje:
Rx =  Vectores en x
Ry =  Vectores en y
3. Encontramos el vector suma total o
“Resultante” por medio del
Teorema de Pitágoras.
2
Y
2
x
2
RRR 
1. Dado el vector A de módulo 20
unidades, hallar sus componentes
rectangulares (X, Y)
Rpta.
2. Dos vectores de módulos 10N y 6
N forman entre sí un ángulo de
60º. Hallar el módulo del vector
resultante
Rpta.

4. Ficha de Aprendizaje FISICA -2014
4
3. La máxima resultante de dos
vectores es 14 y su mínima
resultante es 2. ¿Cuál será la
resultante cuando formen un
ángulo de 90º?
Rpta.
4. La máxima resultante de dos vectores
es 8 y su mínima resultante es 2. ¿Cuál
será el módulo de la resultante cuando
formen un ángulo de 60º?
Rpta.
5. En el sistema vectorial mostrado, halle
el módulo del vector resultante.
Rpta.
6. Halle la medida del ángulo “” sabiendo
que el módulo del vector resultante es
igual a cero
Rpta.
7. En el sistema vectorial mostrado,
hallar la medida del ángulo “”, tal
que, el vector resultante se
encuentre en el eje X.
Rpta.
8. En el sistema vectorial mostrado,
halle el módulo del vector
resultante
A = 10; B = 10; C = 5
Rpta.
9. Sabiendo que: A = 2 y B = 2. Hallar el
módulo del vector suma |A + B| = ?
Rpta.

5. FISICA 5° - 2014 I.E. SV. GALENOs
SICUANI - 2014 5
10. Los puntos A, B y C determinan un
triángulo equilátero de lado 3m. Halar
el módulo del vector resultante.
Rpta.
11. El lado de cada cuadrado es igual a la
unidad de medida. Hallar |a +b |.
Rpta.
12. Sabiendo que: m AB = mBC ; m
OB = 3; hallar el módulo del
vector resultante
Rpta.
13. En el sistema vectorial mostrado,
hallar la dirección del vector
resultante, respecto del eje x
positivo
Rpta.
14. Hallar la medida del ángulo , tal
que, el módulo del vector
resultante sea menor posible
Rpta.
15. En el sistema vectorial mostrado,
hallar el módulo del vector
resultante.
Rpta.

6. Ficha de Aprendizaje FISICA -2014
6
1. Dado el vector V de módulo 30
unidades; hallar sus componentes
rectangulares (X e Y)
A) (24; 18) B) (–24; –18)
C) (–24; 18) D) (24; –18)
E) (0; 30)
2. La máxima resultante de dos
vectores es 17 y su mínima
resultante es 7. ¿Cuál será la
resultante cuando forme un ángulo
de 90º?
A) 10 B) 11 C) 12
D) 13 E) 15
3. En el sistema vectorial mostrado,
hallar el módulo del vector
resultante
A) 6 B) 8 C) 10
D) 2 E) 12
4. En el sistema vectorial mostrado,
hallar el módulo del vector
resultante
A) 7 B) 17 C) 15
D) 13 E) 11
5. En el sistema vectorial mostrado,
la resultante es nula. Halle la
medida del ángulo “” y el módulo
del vector F.
A) 30º y 15 B) 37º y 20º
C) 37º y 15 D) 37º y 25
E) 53º y 15
6. Sabiendo que el vector resultante
se encuentra en el eje vertical,
halle el módulo del vector
resultante.

7. FISICA 5° - 2014 I.E. SV. GALENOs
SICUANI - 2014 7
A) 5 B) 10 C) 15
D) 20 E) 25
7. Si la resultante de los vectores se
encuentra sobre el eje vertical
“Y”, halle el módulo del vector “C”
| A| = 210 y |B| = 10
A) 10 B) 20 C) 30
D) 40 E) 50
8. Los puntos A, B y C determinan un
triángulo equilátero de lado 2 m.
Hallar el módulo del vector
resultante.
A) 2 m B) 4 m C) 6 m
D) 8 m E) 0
9. Hallar el módulo del vector
resultante:
| a | = |b | = |c | = 3
A) 3 B) 6 C) 9
D) 12 E) 15
10. En el sistema vectorial mostrado,
hallar el módulo del vector
resultante. El lado de la cuadrícula
es igual a la unidad de medida
A) 0 B) 1 C) 2
D) 3 E) 4