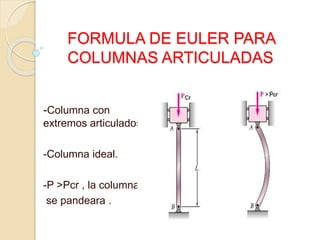
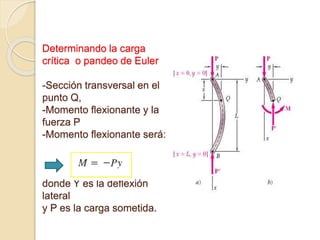
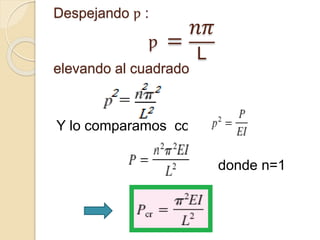
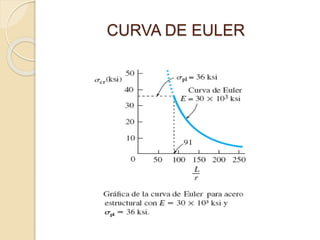
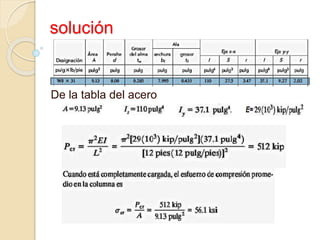
La fórmula de Euler describe el pandeo de una columna articulada en sus extremos. Se presenta la ecuación diferencial que rige el momento flector de la columna y se resuelve para tres casos posibles. La carga crítica se obtiene al igualar la solución a una función seno con las condiciones de frontera. Esto lleva a que la relación entre la carga crítica y las propiedades geométricas y mecánicas de la columna es proporcional a (EI/L2).

1. FORMULA DE EULER PARA
COLUMNAS ARTICULADAS
-Columna con
extremos articulados.
-Columna ideal.
-P >Pcr , la columna
se pandeara .

2. Determinando la carga
crítica o pandeo de Euler
-Sección transversal en el
punto Q,
-Momento flexionante y la
fuerza P
-Momento flexionante será:
donde Y es la deflexión
lateral
y P es la carga sometida.

3. La carga crítica (Pcr)
Para determinar las cargas críticas y la forma
pandeada de la columna , se debe usar la curva de
la flexión de una viga, Son aplicable a una columna
pandeada debido a que la columna se flexiona como
una viga, se elige la ecuación diferencial del
momento flexionante que es :
donde M: momento flector
E: Módulo de elasticidad
I : Momento de inercia
EI: Es la rigidez a la
flexión

4. Entonces reemplazando M quedaría
Ecuación diferencial
homogénea de 2 orden
con coeficientes constantes
Para resolver esto , se pueden dar 3 casos:
- Cuando las raíces sean diferentes
- Cuando las raíces son iguales
- Cuando las raíces seas complejas conjugadas

5. haremos un cambio
de variable
Resolviendo :
m1,2=
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
m1,2=
± 4ƿ2(−1)
2

6. Como las raíces son complejas conjugadas,
estamos en el 3 caso,
Donde se cumple que
m1=α +β1
m2=α – βI
en la ecuación general:
y =C1 𝑒α𝑥
sen(βx) + C2 𝑒α𝑥
cos(βx)
Analizamos con las condiciones de frontera del
grafico en los extremos A y B
En A (x=0, y=0)
En B (x=L, y=0)

7. en A 0 =C1sen(0) + C2cos(0)
0 = C2
en B y =C1sen(ƿx)
0 = C1sen(ƿL)
Analizando , pueden ocurrir 2 cosas
En el 1er caso es que C1=0 , si ocurre
eso , se reduce a y=0 y la columna es
recta.
En el 2do caso es que sen(ƿL)=0 , y eso
implica que ƿL=0,𝜋, 2𝜋,etc. , equivalente a
donde

8. Despejando ƿ :
ƿ =
𝑛𝜋
L
elevando al cuadrado
Y lo comparamos con
donde n=1

9. De la ecuación se deduce :
Hallamos el esfuerzo crítico
recordar
I=A𝑟2
donde L/r es la relación de esbeltez 150> L/r > 30

10. CURVA DE EULER

11. Comentarios generales
Cuando se va a elegir el I en el momento de inercia , se debe
elegir el menor I dado que por ahí se pandeara la columna, los
ingenieros tratan de lograr un equilibrio manteniendo los
momentos de inercia en todas las direcciones así que figuras
circulares o cuadradas harían columnas excelentes .

12. Ejemplo 1

13. solución
De la tabla del acero

14. Ejemplo 2
Solución
Usando la fórmula del FS
Pcr = (2.5) .100kN = 250Kn
I = a4/12 ,