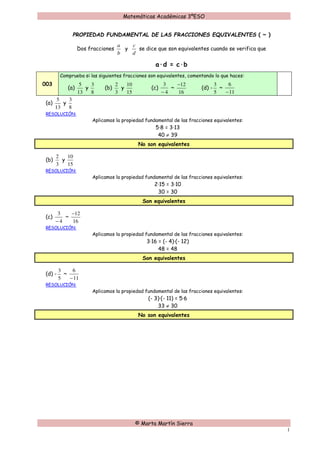
Este documento explica la propiedad fundamental de las fracciones equivalentes. Dos fracciones a/b y c/d son equivalentes si a·d = b·c. El documento proporciona ejemplos de comprobar si pares de fracciones son equivalentes aplicando esta propiedad. Resuelve cuatro ejemplos, determinando que dos pares de fracciones son equivalentes mientras que los otros dos pares no lo son.

1. Matemáticas Académicas 3ºESO
© Marta Martín Sierra
1
PROPIEDAD FUNDAMENTAL DE LAS FRACCIONES EQUIVALENTES ( ~ )
Dos fracciones
b
a
y
d
c
se dice que son equivalentes cuando se verifica que
a·d = c·b
003
Comprueba si las siguientes fracciones son equivalentes, comentando lo que haces:
(a)
13
5
y
8
3
(b)
3
2
y
15
10
(c)
4
3
−
~
16
12−
(d) -
5
3
~
11
6
−
(a)
13
5
y
8
3
RESOLUCIÓN:
Aplicamos la propiedad fundamental de las fracciones equivalentes:
5·8 = 3·13
40 ≠ 39
No son equivalentes
(b)
3
2
y
15
10
RESOLUCIÓN:
Aplicamos la propiedad fundamental de las fracciones equivalentes:
2·15 = 3·10
30 = 30
Son equivalentes
(c)
4
3
−
~
16
12−
RESOLUCIÓN:
Aplicamos la propiedad fundamental de las fracciones equivalentes:
3·16 = (- 4)·(- 12)
48 = 48
Son equivalentes
(d) -
5
3
~
11
6
−
RESOLUCIÓN:
Aplicamos la propiedad fundamental de las fracciones equivalentes:
(- 3)·(- 11) = 5·6
33 ≠ 30
No son equivalentes