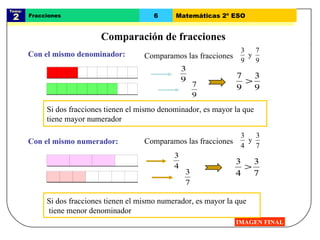
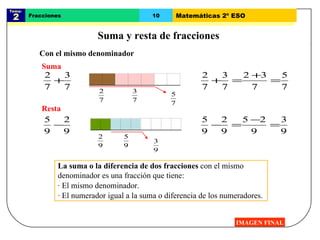
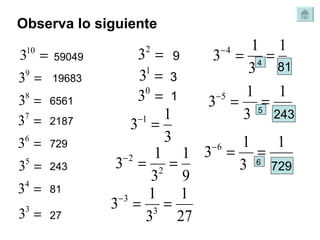
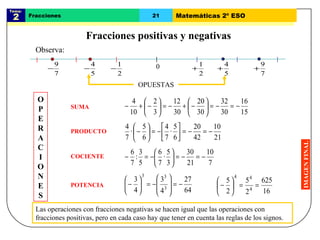
El documento trata sobre las fracciones en matemáticas de 2o de ESO. Explica conceptos como fracciones equivalentes, comparación y ordenación de fracciones, suma y resta de fracciones con el mismo y distinto denominador, multiplicación, división, potencias y raíces cuadradas de fracciones, y operaciones con fracciones positivas y negativas. Incluye ejemplos y problemas resueltos para cada tema.

1. NÚMEROS RACIONALES Tema: 2 Fracciones 1 Matemáticas 2º ESO

2. Tema: 2 Fracciones 2 Matemáticas 2º ESO

3. Tema: 2 Fracciones 3 Matemáticas 2º ESO

4. Para comprobar si dos fracciones son equivalentes basta ver si cumplen alguna de las condiciones anteriores Tema: 2 Fracciones 4 Matemáticas 2º ESO Fracciones equivalentes IMAGEN FINAL Dan el mismo cociente: Tienen iguales productos cruzados: 8 · 10 = 20 · 4 Tienen la misma fracción irreducible: Actúan de la misma manera: Representan lo mismo: Veamos las fracciones Las fracciones son equivalentes.

5. Para obtener fracciones equivalentes a una dada: · Se multiplican o dividen sus términos por el mismo número. Tema: 2 Fracciones 5 Matemáticas 2º ESO Cómo obtener fracciones equivalentes IMAGEN FINAL Obtenemos fracciones equivalentes a son fracciones reducidas de son fracciones ampliadas de es la fracción irreducible de

6. Tema: 2 Fracciones 6 Matemáticas 2º ESO Comparación de fracciones IMAGEN FINAL Con el mismo denominador: Si dos fracciones tienen el mismo denominador, es mayor la que tiene mayor numerador Si dos fracciones tienen el mismo numerador, es mayor la que tiene menor denominador Con el mismo numerador: Comparamos las fracciones Comparamos las fracciones

7. Tema: 2 Fracciones 7 Matemáticas 2º ESO Reducción de fracciones a común denominador IMAGEN FINAL Hemos multiplicado los dos términos de cada fracción por los denominadores de las otras dos. El denominador debe ser múltiplo de 3, 4 y 6; por ejemplo 3 · 4 · 6 Queremos obtener fracciones equivalentes a con la condición de que tengan el mismo denominador.

8. Tema: 2 Fracciones 8 Matemáticas 2º ESO Reducción de fracciones a m.c.m. IMAGEN FINAL m.c.m. (3, 4, 6) = 12 También podemos tomar como denominador común el menor de los múltiplos comunes de los denominadores: el m.c.m. de los denominadores. 12 = 3 · 4 12 = 4 · 3 12 = 6 · 2 Para reducir varias fracciones a común denominador: 1.º Se halla el m.c.m. de los denominadores. 2.º Se divide el m.c.m. entre cada uno de los denominadores y el resultado se multiplica por el numerador correspondiente. Para las mismas fracciones, se tendrá: 4 4 3 3 2 2 Las fracciones son equivalentes a las dadas y tienen el mismo denominador: el mínimo común denominador.

9. Tema: 2 Fracciones 9 Matemáticas 2º ESO Comparación de fracciones cualesquiera IMAGEN FINAL Para comparar dos o más fracciones cualesquiera: 1.º Se reducen a común denominador. 2.º Es mayor la que tiene mayor numerador. Para ello reducimos a común denominador: m.c.m. (3, 6, 5) = 30. De otra forma Para comparar fracciones podemos comparar los cocientes que resultan al dividir en cada fracción el numerador entre el denominador. Luego: > > Comparamos Como , entonces:

10. Tema: 2 Fracciones 10 Matemáticas 2º ESO Suma y resta de fracciones IMAGEN FINAL Suma La suma o la diferencia de dos fracciones con el mismo denominador es una fracción que tiene: Con el mismo denominador Resta · El mismo denominador. · El numerador igual a la suma o diferencia de los numeradores.

11. Tema: 2 Fracciones 11 Matemáticas 2º ESO Suma y resta de fracciones con distinto denominador IMAGEN FINAL Suma Para sumar o restar fracciones con distinto denominador: Resta · Se reducen a un común denominador. · Se suman o restan las fracciones obtenidas. 1 . Las reducimos a común denominador: m.c.m. (6, 4) = 6 · 2 = 4 · 3 = 12. 2 . Las sumamos. 1 . Las reducimos a común denominador: 12 · 4 = 8 · 6 = 48. 2 . Las restamos.

12. Tema: 2 Fracciones 12 Matemáticas 2º ESO

13. Tema: 2 Fracciones 13 Matemáticas 2º ESO Multiplicación de fracciones IMAGEN FINAL El producto de dos fracciones es una fracción que tiene: · El numerador igual al producto de los numeradores · El denominador igual al producto de los denominadores. Decimos: la mitad de dos tercios es dos sextos. Escribimos: Ricardo merienda la mitad de los de la tableta de chocolate. ¿Qué fracción de tableta representa el chocolate que ha comido Ricardo? Ha tomado de tableta. Mitad de Mitad de

14. Tema: 2 Fracciones 14 Matemáticas 2º ESO Fracciones inversas de una dada IMAGEN FINAL Dos fracciones son inversas cuando su producto es igual a la unidad. Observa: Ejemplos: Como los productos: ¿Cuál es fracción que multiplicada por es igual a 1? Se dice que es la fracción inversa de . De igual modo, es la fracción inversa de . son fracciones inversas entre sí. Las fracciones son inversas, respectivamente, de

15. Tema: 2 Fracciones 15 Matemáticas 2º ESO División de fracciones IMAGEN FINAL El cociente de dos fracciones es igual al producto del dividendo por la inversa del divisor. EJERCICIO PROPUESTO ? Comprobación: Haz las siguientes operaciones y expresa el resultado en forma irreducible: La fracción que buscamos es el resultado de ¿Cuál es fracción que multiplicada por es igual a ? · La fracción buscada es a) b) a) b)

16. Tema: 2 Fracciones 16 Matemáticas 2º ESO

17. Tema: 2 Fracciones 17 Matemáticas 2º ESO

18. Tema: 2 Fracciones 18 Matemáticas 2º ESO Potencias de fracciones IMAGEN FINAL Para elevar una fracción a una potencia se elevan el numerador y el denominador a dicha potencia. Ejemplos: Escribimos abreviadamente: Calculamos: Observa que es un producto de cuatro factores iguales. es una potencia. Su base es y su exponente 4.

19. 2 - 4 Ejemplos 0,6 - 3 (-7) - 10 - 2 Propiedad : Potencia con Exponente Negativo. Tema: 2 Fracciones 19 Matemáticas 2º ESO

20. ¿Qué hace la propiedad? 2 - 4 0,6 - 3 = __ 1 2 4 = __ 1 0,6 3 (-5) 4 = ___ 1 - (-5) - 4 7 = 7 __ 3 2 - 2 3 __ Propiedad : Potencia con Exponente Negativo. En General ó Tema: 2 Fracciones 20 Matemáticas 2º ESO

21. Así podemos aplicar la propiedad varias veces sobre un mismo número . 7 2 = __ 1 7 -2 7 2 = __ 1 7 -2 = 7 -2 = __ 1 7 2 7 -2 = __ 1 7 2 = Propiedad : Potencia con Exponente Negativo. Tema: 2 Fracciones 21 Matemáticas 2º ESO Toda potencia de exponente negativo es igual a la unidad dividida por la misma potencia con exponente positivo.

22. Ejercicios: Cambiar el signo del exponente Propiedad : Potencia con Exponente Negativo. Tema: 2 Fracciones 22 Matemáticas 2º ESO

23. Observa lo siguiente 1024 512 256 128 64 32 16 8 4 2 1 4 16 5 32 6 64 Tema: 2 Fracciones 23 Matemáticas 2º ESO

24. Observa lo siguiente 59049 19683 6561 2187 729 243 81 27 9 3 1 4 81 5 243 6 729

25. Tema: 2 Fracciones 19 Matemáticas 2º ESO Cuadrados y raíz cuadrada de una fracción IMAGEN FINAL La raíz cuadrada de una fracción es un número cuyo cuadrado es igual a la fracción. Observa: Observa que es el cuadrado de la fracción También podemos pensar que representa un cuadrado de superficie igual a es la fracción cuyo cuadrado es igual a es la raíz cuadrada de

27. Tema: 2 Fracciones 21 Matemáticas 2º ESO Fracciones positivas y negativas IMAGEN FINAL OPERACIONES 0 OPUESTAS SUMA PRODUCTO COCIENTE POTENCIA Observa: Las operaciones con fracciones negativas se hacen igual que las operaciones con fracciones positivas, pero en cada caso hay que tener en cuenta las reglas de los signos.